с.м.чернов_квантовая механика

Тогда вековое уравнение примет диагональный вид:

решением которого являются искомые поправки:

относительное смещение возбужденного уровня с учетом (2) равны:

где мы рассмотрели утрированный случай Z 100 . Как видно, поправки к уровням энергии водородоподобных атомов, даже при Z 100 , являются

ментом 1 ≠ 0 большую часть времени находится вне области ядра, и искажение кулоновского поля практически не влияет на его состояние.

181

Следует, однако, заметить, что влияние конечных размеров ядра может быть весьма существенным в случае так называемых мезоатомов, когда вблизи ядра движутся не электроны, а мюоны с массой mμ = 207me . Это следу-

ет из оценок:

E1' a13 m3 и E2' a15 m5 .

4.6. Водородоподобный атом помещен в однородное электрическое поле с напряженностью ε, направленное вдоль оси Z . Найти расщепле-

ние первого возбужденного уровня энергии (эффект Штарка).

Решение:

Очевидно, что в данном примере нарушается центральный характер поля. Поэтому следует ожидать расщепление энергии 2р-состояния на три подуровня, соответствующих различным значениям магнитного квантового числа m = 0, ±1.

В однородном электростатическом поле, направленном вдоль оси z, потенциальная энергия взаимодействия электрона с полем равна:

которая и представляет собой оператор возмущения. Как уже отмечалось, первый возбужденный уровень (n=2) является 4-х кратно вырожденным. Поэтому линейные по возмущению поправки к энергии можно найти как решение векового уравнения. Однако, большинство матричных элементов Hmn'

равно нулю. В этом проще всего убедиться, записав волновые функции не в сферических, а в декартовых координатах. Действительно, учитывая связь

I = ∫∫∫dxdydzxk ym zn f (r) .

−∞

182

Если хотя бы один из трех параметров k, m, n является нечетным числом, то I=0. учитывая соотношения (1) и (2), мы легко определим, что отличными от нуля являются лишь матричные элементы H12' = H21' с волновыми функциями

Учитывая явный вид волновых функций и оператора возмущения (1) получаем:

Таким образом, вековое уравнение примет вид:

Последнее уравнение можно представить в виде:

E'2 (E'2 − H12'2 ) = 0 ,

решением которого являются искомые поправки:

ется на три компоненты. Полное снятие вырождения не произошло, так как при наличии поля остается симметрия относительно вращения вокруг направления поля. В результате такого расщепления вместо одной спектральной линии, отвечающей переходу E20 → E10 , мы получили три линии. Данное явле-

ние называется эффектом Штарка.

Из (5) следует, что величина расщепления для водорода ( Z =1) составляет E = E4' −E3' =6eεa ≈3 10−8ε эВ, если ε измеряется в В/см. расщепление мало даже в достаточно сильных полях с напряженностью

ε =104 смВ ( E = 3 10−4 эВ, а разность E20 − E10 ≈10эВ).

183

Задачи к главе V

5.1. Оценить время τ, в течение которого электроны в атоме гелия обмениваются своими квантовыми состояниями. Связать его с обменной энергией А. Спиновыми эффектами пренебречь.

Решение:

Как было показано, состояние электронов в атоме гелия с энергиями

Φ1 – описывает состояние (41.2), когда первый электрон находится в первом

квантовом состоянии, а другой – во втором, Φ2 – определяет такую конфигурацию (41.4), когда электроны обменялись

квантовыми состояниями.

В соответствии с общими принципами квантовой механики эти стационарные состояния можно описывать также волновыми функциями, гармонически зависящими от времени:

где введены обозначения:

Далее, в соответствии с принципом суперпозиции, состояние двухэлектронной системы можно описать и любой линейной комбинацией функций (2), в частности:

произошел обмен первоначальными квантовыми состояниями.

184

квантовый обмен. Учитывая обозначение (3), окончательно получаем:

Таким образом, время обмена квантовыми состояниями обратно пропорционально обменной энергии А, зависящей от степени перекрывания электронных облаков.

Оценки показывают, что в атоме гелия время обмена двух электронов, находящихся в 1s- и 2s- состояниях имеет порядок τ 10−15 c . Если же второй электрон удалить в состояние 10s , то время обмена возрастает до величины τ 10 лет.

Задача 5.2. В возбужденном состоянии атома гелия один электрон находится в 3d -, а другой в 2p -состояниях. Какие состояния атома при

этом возможны?

Решение:

Так как электроны не являются эквивалентными (имеют различные значения l = 2,1), то подсчет возможных термов чрезвычайно прост. Согласно правилу сложения моментов – L =1,2,3 , а полный спин атома S = 0,1. Следовательно, такая система может иметь следующие термы:

1P1; 3P0,1,2 ; 1D2 ; 3D1,2,3; 1F3; 3F2,3,4.

В отсутствии спин-орбитального взаимодействия уровни энергии с различными J в пределах триплетов совпадают.

Задача 5.3. Два электрона находятся в S-состоянии (l = 0) и имеют

одинаковые значения главного квантового числа n1 = n2 = n. Определить спектральный терм атома (основное состояние атома гелия).

Решение:

Если электроны в атоме являются эквивалентными, т.е. имеют одинаковые значения n и l , то при подсчете возможных термов необходимо учитывать принцип запрета Паули.

Так как l1 = l2 = 0 , то орбитальные магнитные квантовые числа так же равны нулю m1 = m2 = 0 . Следовательно, в соответствии с принципом Паули, электроны должны отличаться различными проекциями спинов, например,

ms1 = + 12 , ms2 = −12 . Тогда L = 0, S = 0, J = 0 и возможен лишь единственный

синглетный терм 1S0 . Такое состояние атома гелия называется парагелием. 185

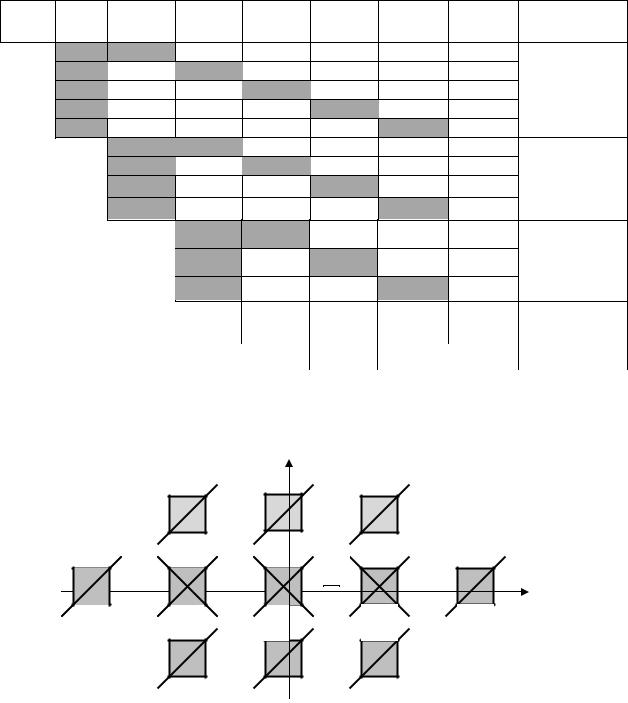
Внутри квадратиков указана мультиплетность состояния. Затем

После исключения этого терма из диаграммы Cлэтера остается всего одно состояние с M L = 0 и M S = 0 , что соответствует значениям L = S = 0 и

J = 0 , т.е. синглетный терм 1S0 . Таким образом, система из двух эквивалентных p-электронов с n1 = n2 = n и l1 = l2 =1 может находиться в состояниях:

3P0,1,2 ; 1D2 ; 1S0 .

Задача 5.5. Вне замкнутых внутренних оболочек атома имеется четыре d-электрона. Определите терм его основного состояния в пренебрежении спин-орбитальными силами.

Решение:

Так как у четырех эквивалентных электронов l = 2 , то ml каждого электрона принимает 5 значений: ml = −2, −1,0, +1, +2, поэтому все четыре

электрона могут иметь одинаковые проекции спина, например, ms = 12 , что обеспечит наибольший спин системы S = 2 . После этого мы должны

187

приписать электронам различные значения ml , которые могли бы обеспечить

4

максимальное M L = ∑mli . Для этого можно взять набор ml = 2,1,0, −1. Тогда

i=1

M Lmax = 2, что соответствует L = 2 , следовательно, искомый терм 5D0,1,2,3,4 .

В отсутствии спин-орбитальных сил этот уровень для различных

J является пятикратно вырожденным.

Задача 5.6. Определить спектральный терм основного состояния атома углерода (Z = 6): C(1s2 2s2 2p2 ).

Решение:

Внутренние s-оболочки атома не вносят вклад в механический момент атома. Внешняя p-оболочка могла бы вместить не 2, а 6 электронов, т.е. меньше половины, тогда в соответствии с задачей 5.4 и правилами Хунда основным термом углерода является терм: 3P0

Отсюда, в частности, следует, что углерод не обладает атомным

магнитным моментом μ = −g e J = 0. m0

188

Задачи к главе VI

6.1. Электрон рассеивается в кулоновском поле точечного ядра с зарядом Ze . Вычислить дифференциальное сечение рассеяния электрона на ядре (формула Резерфорда).

Решение:

В первом борновском приближении при рассеянии частицы массы m в центрально-симметричном поле u(r) дифференциальное сечение рассеяния равно:

Потенциальная энергия взаимодействия электрона с ядром равна:

Однако, непосредственное применение формулы (1) невозможно, т.к. радиус действия кулоновских сил равен бесконечности, и интеграл J в соотношении

(1) расходится. Чтобы преодолеть эту трудность рассмотрим “экранированный” кулоновский потенциал (потенциал Юкава):

который переходит в кулоновский при отсутствии экранировки (a → ∞). Для дальнейшего учтем табличный интеграл вида:

Отсюда, с учетом условия (2), окончательно получаем формулу Резерфорда:

189

Отметим, что эта формула справедлива лишь в нерелятивистском приближе-

нии (v c) и для точечного ядра.

6.2. Рассматривая ядерный потенциал в виде сферической потенциальной ямы радиуса а и глубины -U0 , т.е.

1)Вычислить дифференциальное и полное сечение упругого рассеяния нейтрона на протоне в первом борновском приближении.

2)Оценить порядок сечения рассеяния “тепловых” нейтронов на протонах, используя связь параметров потенциала, полученную в теории дейтрона (задача 3.11):