с.м.чернов_квантовая механика
.pdf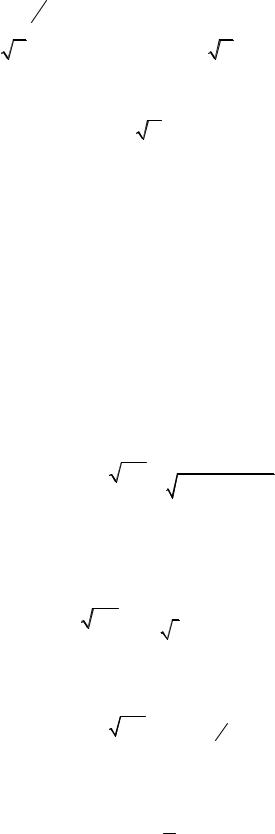
x |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
∫a e−a2 x2 dx ={t ≡ ax}= |
|
∫1 e−t2 dt = Φ(1)= 0,683, где |
|
w1 = 2 ∫0 |
|
ψ |
|
2 dx = |
2a |
2 |
||
|
|
|||||||
|
|
π |
π |
|||||
|
|
|
|
|||||
0 |
|
|
|
|
|
0 |
|
0 |
использовано значение интеграла Френеля:
|
2 |
x |
|
|
Φ(x)= |
∫e−t2 dt. |
(2) |
||
π |
||||
|
0 |
|
||
|
|
|
Тогда вероятность пребывания осциллятора вне классических границ
поля, очевидно, равна: w2 =1 − w1 = 0,317 .
3.5. Вычислить ток холодной эмиссии электронов из металла с энергией Ферми F , помещенного во внешнее постоянное однородное электрическое поле напряженностью ε.
Решение:
При включении электрического поля потенциальная энергия электрона вне металла равна: U (x)=U0 − eεx , где U0 – потенциал на границе металл-
вакуум (х=0). Таким образом, электроны, расположенные на уровне Ферми, отделены от внешней области треугольным потенциальным барьером, который они способны преодолеть в результате туннельного эффекта.
Вычислим вначале коэффициент проницаемости этого барьера:
|
|
|
2 |
2m |
x2 |
|
|
|
|
|
D = D exp |
− |
∫ |
U |
0 |
− eεx − F dx |
, |
(1) |
|||
0 |
|
|
|
h |
|
|
|
|
||
|
|
|
|
|
|
|
||||
|
|
|
|
|
x1 |
|
|
|
|
|
где граничные точки равны: x1 = 0, x2 = U0e−ε F . Введя замену переменных t =U0 − eεx − E , интеграл в условии (1) элементарно вычисляется:
|
|
2 |
2m |
0 |
|
|
|
|
c |
|
|
|
|
D = D exp |
∫ |
tdt = D exp |
− |
, |
(2) |
||||||||
|
|
|
|
||||||||||
0 |
|
|
heε |
|
0 |
|
|
|
|
|
|||
|
|
|
|
|
ε |
|
|
||||||
|
|
|
|
U0 −F |
|
|
|
|
|
|
|
|
|
где параметр с зависит от свойств конкретного металла, и определяется формулой:
c = |
2 2m (U |
0 − F )3 2 |
(3) |
|
3he |
|
|
Аналогично формуле (2), ток холодной эмиссии (вольтамперная характеристика) будет иметь вид:
J= J0 exp −εc .
3.6.Вычислить коэффициент проницаемости потенциального барьера при α-распаде ядра с зарядом (Z + 2)e в случае, когда кинетическая
энергия α-частицы EnU0 , где U0 – высота кулоновского барьера. Срав-
161
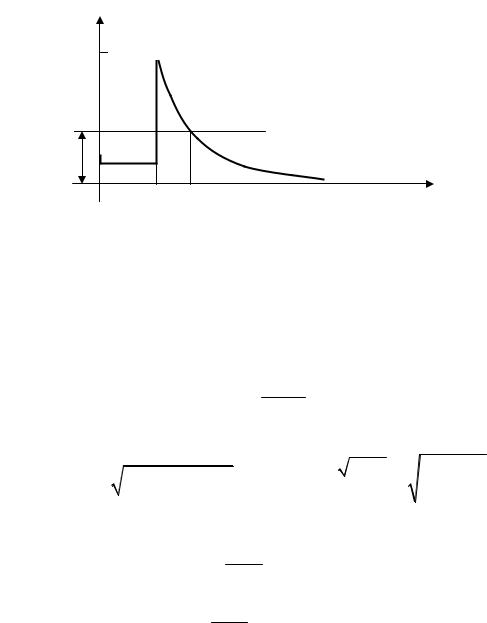


3.8. Частица движется в центральном поле U(r), удовлетворяющему
условию:
limr2U(r)= 0,
r→0
(т.е. растет в нуле не быстрее r12 ). Оценить вероятность нахождения час-
тицы вблизи силового центра (r → 0).
Решение:
Совершая предельный переход (r → 0) в радиальном УШ для функции f (r ), получим уравнение:
d 2 f |
− |
l (l +1) |
f = 0. |
|
dr2 |
r2 |
|||
|
|
Будем искать решение последнего уравнения в виде степенной функции f (r )= Ark , где k – подлежит определению. Подставляя это решение в пре-
дыдущее уравнение, получим условие, которое выполняется в двух случаях: k1 = l +1, k2 = −l . Второе решение не удовлетворяет граничным условиям
f (0)= 0 , и таким образом, решение предыдущего уравнения, удовлетворяю-
щее стандартным условиям, должно иметь вид:
f(r )= Arl +1,
арадиальная волновая функция R (r )= Arl .
Плотность вероятности обнаружение частицы вблизи силового центра в
полях, удовлетворяющих условию задачи, равно:
w(r )= f (r )2 = A2r2(l+1),
т.е. w(r) убывает с ростом l . Физически это можно объяснить возрастанием центробежного отталкивания с увеличением момента импульса частицы.
3.9. Частица движется в центральном поле U(r), исчезающее на бес-
конечности:
lim U(r)= 0 .
r→∞
Оценить вероятность нахождения частицы на далеких расстояниях от силового центра.
Решение:
При r → ∞ радиальное УШ для функции f (r ) примет вид:
d 2 f + 2m0 E f = 0. dr2 h2
164

Будем различать два случая: E ≥ 0 и E ≤ 0 .
В первом случае (E ≥ 0) решение уравнения имеет вид: f (r)= Asin (kr +α),
где введено обозначение: k 2 = 2mh20 E ≥ 0.
Этот случай соответствует сферически расходящимся от центра волнам:
R (r )= A sin (kr +α ) r
и вероятность пребывания частицы на бесконечном удалении от центра w(r ) = A2 sin2 (kr +α ) ≠ 0 не исчезает при r → ∞ (инфинитное движение).
Во втором случае (E ≤ 0) решение уравнения, удовлетворяющее усло-
вию ограниченности, имеет вид:
f (r)= Be−χr ,
где введено обозначение: χ2 = − 2mh20 E ≥ 0.
Плотность вероятности нахождения частицы на больших расстояниях от центра w(r ) = B2e−2χr → 0 при r → ∞, что соответствует связанному состоя-
нию (финитное движение).
Замечание. Можно строго доказать, что волновая функция состояния с
дискретным спектром энергии E квадратично интегрируема, т.е.
∫ψ
 2dV ≤ ∞, а волновые функции состояния сплошного спектра E не могут
2dV ≤ ∞, а волновые функции состояния сплошного спектра E не могут
быть квадратично интегрируемы.
На основании этой теоремы можно сделать общий вывод: в случае E ≥ 0
спектр энергии является сплошным, и частица может уйти на бесконечно удаленные расстояния от центра (ионизация атома); в случае E ≤ 0 частица с дискретным спектром энергии образует связные состояния.
3.10. Вычислить для 1s-электрона в атоме водорода среднеквадратичный разброс координат 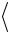 ( r2 )
( r2 )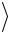 1 2 .
1 2 .
Решение:
Для основного состояния атома водорода (1s-состояние) радиальная волновая функция R10 (r ) равна
|
|
2 |
− |
r |
|
|
(r)= |
a |
|
||
R |
|
e |
0 |
, |
|
|
|||||
10 |
|
a3 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
где a0 – первый боровский радиус.
165
Тогда вводя функцию f10 (r ) = rR10 (r ), можно вычислить
∞ |
|
|
4 |
∞ |
|
3 −2 |
r |
3 |
|
|||
2 |
|
|
a |
|
|
|||||||
r = ∫dr rf |
|
(r)= |
|
∫drr e |
|
0 = |
|
a0 |
||||
|
3 |
|
2 |
|||||||||
0 |
|
|
|
a0 |
0 |
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
r2 = ∫dr r2 f 2 (r)=3a0 , |
|
|
||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
где учтены табличные интегралы вида: |
|
|
|
|
|
|
|
|
||||
∞ |
|
|
|
|
|
|
k! |
|
|
|
|
|
∫ xke−βxdx = |
|
. |
|
|
|
|
||||||
βk +1 |
|
|
|
|
||||||||
0 |
|
|
|
|
|
|
|
|
|
|
||
( r )2 = (r − r |
)2 |
2 = r2 − 2r r + r 2 = r2 − r 2 |
||||||||||
Тогда окончательно получаем: |
|
|
|
|
|
|
|
|
|
|
||
( r )2 |
1 2 = |
3a = 0,78a . |
||||||||||
|
|
|
|
|
4 |
0 |
|
|
|
0 |
|
|
Заметим, что неопределенность положения электрона в атоме соизмери- |
||||||||||||
ма с “размерами” самого атома. |
|
|
|
|
|
|
|
|
|
|
|
|
3.11. Считая, что ядерный потенциал имеет вид сферически- |
||||||||||||
симметричной прямоугольной ямы ширины ro |
и глубины – Uo , найти |
|||||||||||
связь между Uo иro для дейтрона с энергией связи ε=2,226 МэВ. Оценить
Uo , если ro = 2 Фм. Сравнить качественно ядерные силы с электромагнитным взаимодействием.
Решение:
Так как поле U (r) является сферически симметричным, то для решения задачи воспользуемся радиальным УШ. для функции f (r) = rR(r) :
|
d |
2 |
f (r ) |
+ 2μ2 |
|
|
|
|
|
2 |
l (l + |
1) |
|
|
|
||||||
|
|
E −U (r )− |
h |
f (r )= 0, |
(1) |
||||||||||||||||
|
|
|
2 |
|
2 |
|
|||||||||||||||
|
|
dr |
|
h |
|
|
|
|
|
2μr |
|
|
|
|
|
||||||
с граничными условиями: |
|
f (0)= 0; |
f (∞)= 0. |
|
|
|
|
|
|
|
|
|
|
||||||||
В уравнении (1) необходимо положить μ = M |
|
и |
E = −ε . Очевидно, основному |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
= 0 (s-состояние). Случай l ≠ 0 |
||||||
состоянию дейтрона соответствует значение l |
|||||||||||||||||||||
качественно будет рассмотрен ниже в задаче 3.13. |
|
|
|
|
|
||||||||||||||||
Следовательно, в нашем случае уравнение (1) примет вид: |
|
||||||||||||||||||||
|
|
|
|
|
d 2 f (r ) |
− |
M |
ε +U |
( |
r |
f |
( |
r |
) |
= 0. |
(2) |
|||||
|
|
|
|
|
|
|
2 |
||||||||||||||
|
|
|
|
|
dr |
2 |
|
h |
|
|
) |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для выбранной модели сферической прямоугольной ямы потенциал U(r) имеет вид:
166

При наличии двух равенств типа (8) удобнее разделить второе уравне-
ние на первое, т.е. приравнять логарифмические производные ( f ′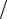 f = (ln f )′)
f = (ln f )′)
в точке r = ro , что приводит к равенству:
ctgβr |
= − |
γ |
|
|
|
(9) |
||
β. |
|
|
||||||
o |
|
|
|
|
|
|
||
Из условий (4) и (6) следует, что отношение |
γ |
= |
|
ε |
n1 , и в приближе- |
|||
|
|
|||||||
|
|
|
|
β |
|
Uo |
||
нии нулевой энергии связи дейтрона мы получаем:
ctgβr = 0; |
βr |
= |
π |
; |
U |
r2 |
= |
π 2h2 . |
(10) |
o |
o |
|
2 |
|
|
o o |
|
4M |
|
Заметим, что наши расчеты зависят от характерной комбинации параметров потенциала Uoro2 , который будем называть эффективностью потенциала.
Для численных оценок, учтем, что из мезонной теории следует, что ro = 2
Фм, тогда из формулы (10) окончательно получаем Uo = 51,2 МэВ. Важно заметить, что энергия связи дейтрона ε = 2,226 МэВ мала по сравнению с глубиной потенциальной ямы, следовательно, приближение нулевой энергии связи является разумным приближением.
Для сравнения ядерных сил с электромагнитным взаимодействием можно оценить, например, потенциальную энергию кулоновского отталкивания двух протонов, находящихся на расстоянии ro = 1,414 Фм:
|
|
U |
кул |
= |
|
e2 |
≈1, 01 |
МэВ. |
(11) |
||
|
|
4πε r |
|||||||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
o o |
|
|
|
|
|
Ответ: Uo ro2 = |
π 2h2 |
; r0 =1, 414Фм, U0 |
= 51, 2 МэВ; U |
|
=1, 01 МэВ. |
||||||
4M |
кул |
||||||||||
|
|
|
|
|
|
|
|
|
|||
3.12.Оценить “эффективные размеры” дейтрона и относительное время нахождения нуклонов в области действия ядерных сил τ
(r < ro = 1,41 Фм).
Решение:
Эффективным размером дейтрона Rd можно назвать такое значение r, при котором нуклонная плотность в ядре падает в e раз. Так как нуклонная плотность на периферии ядра в соответствии с формулой (7) равна f22 (r )= B2 exp (−2γr ), то в соответствии с нашим определением:
R = |
1 |
= |
h |
≈2,2 Фм. |
(1) |
|
|
||||
d |
2γ |
|
2 M ε |
|
|
|
|
|
|||
Следовательно, дейтрон имеет размеры, превышающие радиус действия ядерных сил, и поэтому является “рыхлой” системой. Об этом говорят и
168
оценки относительного времени нахождения нуклонов в области действия ядерных сил τ :
|
τ = |
∫0ro f 2 (r )dr |
= |
|
|
|
∫0ro f12 (r )dr |
|
|
|
|
|
≡ |
|
|
|
J1 |
|
|
, |
|
|
|
|
|
(2) |
|||||||||||
|
|
∞ 2 |
( |
|
) |
r0 |
2 |
|
|
|
∞ |
2 |
|
|
|
|
|
J1 |
+ J |
2 |
|
|
|
|
|
|
|||||||||||
|
|
|
∫0 |
|
|
|
∫0 |
|
|
|
|
(r )dr |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
f |
|
r dr |
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
o |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r0 |
f12 (r )dr |
|
|
|
r0 |
|
|
|
|
A2 |
r0 |
(1 |
−cos 2βr )dr = |
|
A2r |
|
|
|
sin 2βr |
|
|
A2r |
(3) |
||||||||||||||
J1 = ∫0 |
= A2 |
∫0 |
sin2 |
βrdr = |
|
|
∫0 |
|
0 |
|
1 |
− |
|
|
|
0 |
|
= |
0 |
; |
|||||||||||||||||
2 |
2 |
|
|
2βr |
|
2 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|||
|
J2 |
= ∫ |
∞ f22 (r )dr = B2 ∫∞ e−2γr dr = |
B2 |
e−2γr0 |
= |
A2 sin2 βr0 |
|
= |
A2 |
. |
|
|
|
|
|
(4) |
||||||||||||||||||||
|
2γ |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
r0 |
|
|
|
|
|
r0 |
|
|
|
|
|
|
|
|
|
2γ |
|
|
|
|
2γ |
|
|
|
|
|
|
|||||||
В выражении (3) и (4) учтены условия (8) и (10) предыдущей задачи. Из формулы (2) окончательно получаем:
τ = |
ro |
|
= |
ro |
= 0, 24. |
(5) |
|
ro + |
1 |
ro + 2Rd |
|||||
|
|
|
|
||||
|
γ |
|
|
|
|
Следовательно, в области ядерного притяжения нуклоны в среднем находятся лишь 24% времени, а вне потенциальной ямы – 76%. Этот эффект качественно объясняет малость энергии связи дейтрона (ε nUo ) .
Ответ: Rd = 2.2 Фм; τ = 0, 24.
3.13. Показать, что связанного состояния двух нуклонов с относительным орбитальным моментом l ≠ 0 не существует.
Решение:
Необходимым условием того, что NN – система находится в связанном состоянии, является условие отрицательности полной энергии системы (Е < 0). Если l ≠ 0 , то из-за центробежных эффектов должны появляться силы отталкивания, потенциальная энергия которых по порядку величины равно:
Uц.б. |
= |
h2l (l + |
1) |
= 4l (l +1)ε. |
(1) |
2 |
|
||||
|
|
MRd |
|
|
|
Тогда полная энергия дейтрона будет равна:
E = −ε +U |
ц.б. |
=ε 4l (l +1)−1 . |
(2) |
|
|
|
|
|
|
Отсюда видно, что при любых l ≠ 0 (l = 1, 2, 3, ...) энергия Е > 0, и дейтрон не имеет возбужденных уровней энергии.
3.14. Определить явный вид матриц Паули σ$x и σ$y в случае, если матрица σ$z диагональная (z-представление):
169