с.м.чернов_квантовая механика

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Могилёвский государственный университет им. А. А. Кулешова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

h2l (l +1)

(l =0,1,2,...)

.pdf

Скачиваний:

Добавлен:

22.03.2016

Размер:

2.6 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 207 8 9 10 11 12 13 14 15 16 17 18 19 20 > Следующая >>>

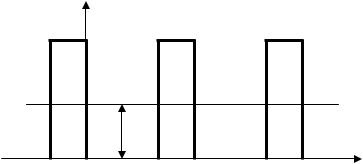
0,		nl ≤ x ≤ nl + a	,	(25.1)
U (x)=	,	nl −b ≤ x ≤ nl
U0

где l = a + b – период решетки; n = 0, ±1, ±2 …±∞ (рис. 8).

U0 U (x)

I II III

-b 0

a l=a+b

l+a 2l

Рис. 8

Рассмотрим движение частицы в таком поле с энергией E ≤U0 . Доста-

точно рассмотреть состояние частицы в областях I, II, III и учесть формулу Блоха:

	ψ (x +l)= eiklψ (x).								(25.2)
Динамика движения частицы описывается стационарным одномерным
УШ:	d 2ψ (x)
	d 2ψ (x)	+ 2m [E −U (x)]ψ (x) = 0 .							(25.3)
	dx2			h2
1) Область I	(−b ≤ x ≤ 0);	U (x)=U0 , тогда:
				d 2ψ1		− λ2ψ	1	= 0,	(25.4)
				dx2		− λ2ψ		= 0,	(25.4)
				dx2
где введено обозначение:
	λ2 =				2m	(U0 − E )≥ 0.			(25.5)
	λ2 =				h2	(U0 − E )≥ 0.			(25.5)
					h2
	ψ	1	(x)= c eλx +c e−λx.						(25.6)
		1				1	2
2) Область II	(0 ≤ x ≤ a); U (x)= 0,
			d 2ψ2			+Q2ψ2 = 0 , где			(25.7)
						+Q2ψ2 = 0 , где			(25.7)
				dx2
						61

		Q2 =	2mE	≥ 0	(25.8)
		Q2 =	2	≥ 0	(25.8)
			h
ψ2		= c3eiQx +c4e−iQx .			(25.9)
3) Область III (a ≤ x ≤ l = a +b);				U (x)=U0 ,	что совпадает с областью I.
Следовательно:
ψ	3	= c eλx + c e−λx			(25.10)
	3	5		6
Свяжем коэффициенты c5 и c6		с коэффициентами c1 и c2 . Для этого учтем ус-

ловие Блоха (25.2) и тот очевидный факт, что если x принадлежит области I, то (x +l) попадает в область III, тогда условие Блоха принимает вид:

	ψ3 (x +l)= eiklψ1 (x), или				(25.11)
c eλxeλl +c e−λxe−λl			= c eikleλx +c eikle−λx .
5	6		1	2
Отсюда получаем искомую связь коэффициентов:
c	= c eikl−λl ;	c	= c eikl+λl .		(25.12)
5	1	6	2
Таким образом,
ψ3 = eikl (c1eλ(x−l) +c2e−λ(x−l )).					(25.13)
Для определения оставшихся коэффициентов c1,c2 ,c3,c4					необходимо об-

ратиться к стандартным условиям, которые сводятся к требованиям:

ψ1 (0)=ψ2 (0) c1 +c2 = c3 +c4

ψ1′(0) =ψ2′ (0) λ(c1 −c2 ) = iQ(c3 −c4 )

(25.14)

ψ2 (a)=ψ3 (a) c3eiQa + c4e−iQa = eikl (c1e−λb + c2eλb )

ψ2′(a)=ψ3′(a) iQ(c3eiQa −c4e−iQa )= λeikl (c1e−λb −c2eλb ).

Система линейных однородных алгебраических уравнений (25.14) имеет нетривиальное решение, лишь, если определитель из коэффициента при неизвестных равен нулю:

1		1		−1	−1
λ		−λ		−iæ	iæ
λ		−λ		−iæ	iæ	=0	(25.15)
−e	−λb	−e	−λb	e	e
ikl	−λb	ikl	−λb	iæa	−iæa
−λe		λe	−λb	iæe	−iæe
ikl−λb		ikl	−λb	iæa	−iæa
				62

После простых, но достаточно громоздких вычислений, мы приходим к трансцендентному уравнению относительно энергии Е вида:

chλbcosæa +	λ2	−æ2	shλbsin æa = cos kl	(25.16)
	2λæ

Уравнение (25.16) является достаточно сложным, и для его исследова-

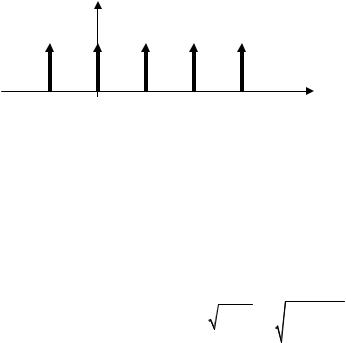
ния совершим предельный переход: ширина барьера b →0 и высота U0 →∞,

так что площадь прямоугольника остается постоянной lim	U	b = const , т.е. за-
b→0	0
U0 →∞

меним прямоугольный периодический потенциал набором δ -функций Дирака

(рис. 9):

U (x)

-a

Рис. 9.

При таком переходе, однако, остается главное свойство потенциала – его периодичность.

Рассмотрим изменение параметров λ2 =

(U0 − E)

и λb при таком пре-

дельном переходе (U0 →∞,b →0):

λ2 →

2mU0

→ ∞ ;

λb = λ2b2 →

2mU0b

b → 0

chλb →1;

shλb →λb .

Тогда уравнение (25.16) значительно упрощается:

cosæa+

λ2

λbsinæa =coska

( l → a + b

→ a ).

2λæ

Введем обозначение

D ≡ λ2b

→U0b =const и уравнение (25.16) сведется к

уравнению:

cos æa + D sin æa = cos ka .

(25.17)

Рассмотрим некоторые варианты решения уравнения (25.17).

1. D U0b = 0 , т.е. U0 =0 барьеры отсутствуют (свободное движение) cosæa =coska в частности, æ = k , что соответствует свободному движе-

нию частицы с волновым числом k , импульсом p = hk и произвольной энер-

гией:
E =	h2k2	=	p2	(сплошной спектр).
E =		=	2m	(сплошной спектр).
	2m		2m
2. D →∞ . Физически это означает наличие изолированных ионов, когда
атомы разделены непроницаемыми барьерами.
				2		2		2	2
sinQa = 0; Qa = πn ;				E =	h	Q	=	π	h	n2; n =1,2K, и мы прихо-
sinQa = 0; Qa = πn ;				E =			=		2	n2; n =1,2K, и мы прихо-
					2m			2ma

дим к дискретным уровням энергии изолированных атомов в модели бесконечно глубокой потенциальной ямы ширины а.

3. 0 < D < ∞ (частично прозрачные барьеры).					Для удобства введем
обозначение: D = tgα .
Тогда левая часть уравнения (25.17) примет вид:
cosQa + tgα sinQa =	cosα cosQa +sinα sin æa			=	cos(Qa −α)	.
		cosα
					cosα
Следовательно, уравнение (25.17) запишется в виде:
		cos(æa−α)	=coska		(25.18)

		cosα

Так как coska ≤1, то решения уравнения (25.18) будут заключены в пределах

границ:

−cosα ≤cos(æa −α) ≤cosα

−α +πn ≤æa −α ≤α +πn

πn ≤æa ≤πn +2α

					æа
0 2α π			π+2α

Таким образом, мы приходим к зонной структуре энергетических уровней, т.е. чередование разрешенных и запрещенных зон.

§26. Общие свойства движения

вцентрально-симметричных полях

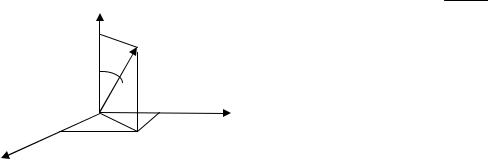
Поле U=U(r) называется центрально-симметричным, если потенциальная энергия частицы зависит лишь от расстояния до некоторого силово-

го центра и не зависит от углов. Примером центрального поля является кулоновская энергия взаимодействия электрона с ядром:

	z
	r
0	ϑ
0	y

Рис. 10

менных имеет вид:

x =rsinθcosϕ;

U (r)= − Ze2 . 4πε0r

В центральных полях весь анализ удобно проводить в сферических коорди-

натах r,ϑ,ϕ (рис. 10).

Область изменения этих перемен-

ных составляет:

0 ≤ r ≤∞; 0 ≤θ ≤π; 0 ≤ϕ ≤ 2π.

Связь декартовых и сферических пере-

y =rsinθsinϕ; z =rcosθ.

Элемент объема: dV = dxdydz = r2dr sinθdθdϕ = r2drdΩ..

Оператор Лапласа:

∂

sinθ

∂

(26.1)

∂x

∂y

∂z

θ ∂ϕ

∂r

sinθ ∂θ

∂θ

sin

Для дальнейшего удобно ввести следующие обозначения:

∂

1 ∂

∂

∂ 2

r =

θ =

sinθ

ϕ =

sinθ ∂θ

∂ϕ

∂r

∂θ

. (26.2)

Тогда выражение (26.1) можно записать в компактной форме:

θ ,ϕ

где

(26.3)

r 2

θ ,ϕ

θ +

ϕ .

(26.4)

sin2 θ

Пусть частица массы m0 движется в некотором произвольном центральном поле U(r). Движение микрочастицы описывается трехмерным стацио-

нарным уравнением Шредингера:

ΔΨ(r,θ,ϕ)+	2m0	E −U (r) Ψ(r,θ,ϕ)= 0 ,	(26.5)
	h2

или с учетом обозначения (26.3):

Ψ(r,θ,ϕ)+

Ψ(r,θ,ϕ)

2m0

E −U

(r) Ψ(r,θ,ϕ)= 0 .

(26.6)

θ,ϕ

Будем искать решение этого уравнения методом разделения перемен-

ных.

Для этого представим волновую функцию в виде произведения:

Ψ(r,θ,ϕ) = R(r)Y (θ,ϕ).

(26.7)

Подставляя эту функцию в уравнение (26.6), получаем:

θ,ϕ

Y +

2m0

[E −U (r)]RY = 0.

Умножим все члены последнего уравнения на

[E −U (r)]r

= −

θ,ϕY

= λ = const .

В последнем уравнении левая часть зависит только от r, а правая лишь

от угловых переменных

θ,ϕ . И это равенство должно выполняться при всех

значениях (r, θ , ϕ ), но это возможно лишь в том случае, если правая и левая части равны λ = const . Тогда мы приходим к двум независимым уравнениям:

	r R (r ) +	2 m 0			λ	h	2
		2 m 0	E	− U ( r ) −	λ	h		R ( r ) = 0;
		2	E	− U ( r ) −	2	2 m 0		R ( r ) = 0;
		h			r	2 m 0		(26.8)

θ ,ϕ Y (θ ,ϕ ) + λY (θ ,ϕ ) = 0 .

Отсюда видно, что силовое поле U(r) определяет поведение лишь радиальной части волновой функции R(r), поэтому это уравнение называется ра-

диальным уравнением Шредингера. При этом угловая частьY (θ,ϕ) является

универсальной функцией для всех центрально симметричных полей.

Рассмотрим уравнение для угловой части волновой функции Y (ϑ,ϕ):

	1
θ +		ϕ Y (θ,ϕ) + λY (θ,ϕ) = 0 .
θ +	sinθ	ϕ Y (θ,ϕ) + λY (θ,ϕ) = 0 .
	sinθ

Разделим переменные и в этом уравнении. Для этого запишем угловую часть в виде произведения двух функций: Y (θ,ϕ) =θ (θ)Φ(ϕ).

ΦΔθθ + sin12 θ θ ϕΦ + λθΦ = 0 .

Умножим все члены уравнения на sin2 θ :

θ Φ

sin2 θ	θ	θ	+ λsin2	θ = −	ϕΦ	= m2	= const ,
	θ				Φ

где мы ввели вторую постоянную разделения m2 (не путать с массой частицы m0 !). Отсюда получаем два независимых уравнения:

			θθ + (λ −		m	2	)θ = 0;
						2

					sin2 θ			(26.9)
					sin2 θ			(26.9)
			2	Φ = 0.
			ϕΦ + m	Φ = 0.
Найдем решение последнего уравнения:
	d 2Φ(ϕ)	+ m2Φ(ϕ) = 0 Φ (ϕ ) = c0 e ± imϕ .
	2	+ m2Φ(ϕ) = 0 Φ (ϕ ) = c0 e ± imϕ .
	dϕ

Если число m можем принимать как положительные, так и отрицательные значения, то общее решение можно записать в виде одной экспоненты:

Φ(ϕ) = c0eimϕ .

(26.10)

Как и любая волновая функция, Ф(φ) должна удовлетворять стандартным условиям, в частности, условию однозначности положения φ. Для этого необходимо потребовать выполнения условия:

Φ (ϕ ) = Φ (ϕ + 2π ) c 0 e im ϕ = c 0 e im ϕ e im 2 π e i 2 π m = 1 , но по-

следнее возможно, если m = 0 ±1± 2 ±... ± ∞. В дальнейшем, параметр m бу-

дем называть магнитным квантовым числом.

Рассмотрим, наконец, решение уравнения для функции Θ(ϑ) (26.9).

Опуская математические подробности, приведем лишь окончательные результаты.

Уравнение (26.9) имеет решение, удовлетворяющее стандартным ус-

ловиям, если выполнены два требования:

1.λ =l(l +1) , где l=0,1,2,...;

2.m ≤ l , т.е. m = 0,±1,±2,... ±l и, следовательно, m принимает (2l+1)

дискретное значение.

В дальнейшем, параметр l будем называть орбитальным квантовым числом. При этом решения уравнения имеют вид: Θ(ϑ) = Θlm (ϑ) = cPl m (cosθ ),

где Pl m (x) – присоединенные полиномы Лежандра:

Pm (x)= (1

− x2 )m2

dl+m

(x2 −1).

(26.11)

dxl+m

2l l!

Коэффициенты с и с0 найдем из условия нормировки:

∫

2 dV = ∫

2 r 2 dr sin θ dθ dϕ = ∞∫

2 r 2 dr π∫

2 sin θ dθ

2∫π

2 d ϕ = 1

c =

;

c =

(2l +1)(l − m)

2π

2(l + m)!

Приведем некоторые частные примеры функции Θlm (θ ):

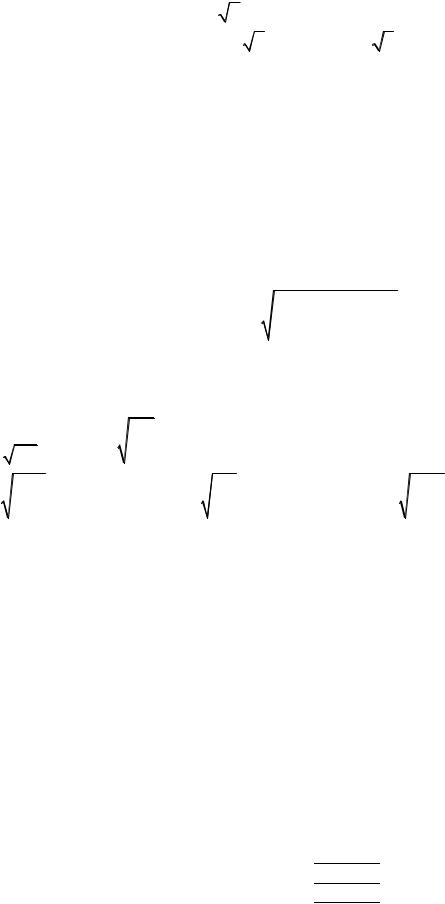
1) l = 0, m = 0; Θ00 =	1	;
1) l = 0, m = 0; Θ00 =	2	;
	2
2) l =1, m = 0,±1; Θ0	=	3	cosθ, Θ±1	= ±	3	sinθ.
2) l =1, m = 0,±1; Θ0	=		cosθ, Θ±1	= ±		sinθ.
1		2	1		2
		2			2

Наконец, отметим некоторые общие свойства полиномов Лежандра:

1) Pm	(−cosθ )= (−1)l+m Pm (cosθ );
l				l
2) xPm =		(l + m)Pm	+	(l − m +1)	Pm	;
l		2l +1 l−1		2l +1	l+1

3) +∫1 Plm (x)Pl′m′ (x)dx =δll′δmm′; ( условиеортонормированности)

−1

(26.12)

(26.13)

Таким образом, в любых центральных полях угловая часть волновой функции определяется двумя дискретными индексами l и m , и имеет вид:

Y (θ ,ϕ ) = Y

(θ ,ϕ ) = θ

(θ )Φ

(ϕ ) =

(2l + 1)(l − m )!

(cosθ )e

imϕ

. (26.14)

4π (l + m )! l

Эта функция определяет положение точки на сфере фиксированного радиуса, поэтому ее называют шаровой функцией. Для справочных целей приведем

примеры шаровых функций Y m

для наименьших значений l = 0,1,2.

Y 0

;

Y 0 =

cosθ; Y ±1 = ±sinθe±iϕ ;

4π

(26.14)

±1

±iϕ

±2

±i2ϕ

(3cos

ϑ −1); Y2

= ±

8π cosθ sinθe

; Y2

= ±

sin

ϑe

16π

32π

Таким образом, в любом центрально-симметричном поле полная вол-

новая функция частицы в сферических координатах должна иметь вид:

ψ (r,ϑ,ϕ) = R(r )Y m (ϑ,ϕ),	(26.15)
l

где Ylm – известная шаровая функция, зависящая от орбитального квантового числа l = 0,1,2,... ∞ и магнитного числа m = 0,±1,±2,... ±l , а радиальная часть волновой функции R(r) определяется видом центрального потенциала U (r ),

и удовлетворяет радиальному уравнению Шредингера:

(

h l

l +1

E −U (r )−

R = 0 .

(26.16)

2m0r

Замечание. В спектроскопии атомов и молекул исторически установилось соглашение, когда значение орбитального квантового числа указывают не в виде цифры, а в виде определенной буквы латинского алфавита, как это указано в таблице:

Значение l	0	1	2	3	4	5	6
Символ состояния	s	p	d	f	g	h	i

Например, фраза “электрон находится в d -состоянии” означает, что

орбитальное число l = 2, а магнитное – может иметь одно из пяти значений

m= 0,±1,±2.

§27. Операторы момента импульса, их собственные функции

исобственные значения

Оператор момента импульса ранее был определен в виде формального определителя:

L^ = r ^ ×p^ =	i	j	k
L^ = r ^ ×p^ =	x$	y^	z$	,
	p^ x	p^ y	p^ z

из которого легко определяются операторы всех проекций и квадрата момента импульса:


Lx	= y Pz	− z Py ,	Ly	= z Px	− x Pz ,	Lz	= x Py	− y Px ,	(27.1)

			L2 =L2 x +L2 y + L2 z .						(27.2)

Учитывая коммутационные свойства операторов координаты и импульса:

x$	, y^		= 0;	p^	x	, p^		= 0;	x^ , p^		= ih,
					x		y			x

не сложно доказать коммутационные соотношения вида:

	$	$			$		$ $			$		$		$		$	(27.3)
Lx , Ly				= ihLz ; Lz , Lx					= ihLy ;		Ly		, Lz		= ihLx ;		(27.3)

			$2	$		= 0;	$2		$	= 0;		$	2	$		= 0.	(27.4)
		L		, Lx		= 0;	L	, Ly		= 0;		L		, Lz		= 0.	(27.4)

Из приведенных соотношений следуют два важных вывода:

1.Невозможность одновременного измерения двух любых проекций момента импульса.

2.Возможность измерения квадрата момента импульса вместе с любой своей проекцией.

В дальнейшем будем считать измеримыми L2 и Lz . Покажем, что шаровая функция Yl m (θ,ϕ) = Plm (cosθ)eimϕ является собственной функцией опера-


торов L2	, L . Запишем операторы L2				, L в сферических координатах:
	z				z
			∂
	L	= −ih	∂	;	L2 = −h2		.	(27.5)
	L	= −ih		;	L2 = −h2	θ,ϕ	.	(27.5)
	z		∂ϕ			θ,ϕ
			∂ϕ

	∂
Lz Yl m (θ,ϕ)= −ih∂ϕ Pl m (cosθ )eimϕ = −ihPl m (cosθ )eimϕ (im)= hmYlm (θ,ϕ). (27.6)
	69

Отсюда следует физический смысл магнитного квантового числа m :

		Lz = hm.			(27.6)
Учитывая соотношение (26.8), т.е.		θ,ϕ	Y m	= −λY m = −l(l +1)Y m , имеем:
			l	l	l
			Y m = h2l(l +1)Y m .		(27.7)
L2 Y m	= −h2
l		θ ,ϕ l		l
Таким образом, отсюда определим физический смысл орбитального
квантового числа l :	L2	= h2 l (l + 1) .
					(27.8)

В частности, если электрон находится в d-состоянии, это означает, что l = 2, L = h 6 и проекция Lz может принимать пять значений Lz = 0 ± h± 2h.

§28. Пространственный ротатор

Ватомной и ядерной физике часто возникают задачи описания вращательного движения (вращение молекул, деформированных ядер и т.д.). Простейшей моделью такого движения можно считать свободное движение частицы массы m0 по сфере заданного радиуса R0 (пространственный ро-

татор).

Эта задача – есть пример движения в центральном поле. Тогда, в соответствии с общей теорией, в.ф. частицы должна иметь вид:

ψ m (r,ϑ,ϕ) = R(r )Y m (ϑ,ϕ),		(28.1)
l	l

где R(r) является решением радиального уравнения Шредингера (26.16):

Но так как

(

h l

l +1

E −U (r )−

R = 0 .

2m0r

r = R0 = const,

то и R(r ) = R(Ro ) = const. Так как потенци-

альная энергия определена с точностью до произвольной аддитивной постоянной, то можно положить U (r) =U (R0 ) = 0. Тогда, из радиального уравне-

ния Шредингера сразу получаем возможные значения энергии вращательного движения:

Таким образом, энергия является дискретной величиной, которая определяется только орбитальным квантовым числом l и не зависит от магнитного числа m (вырождение по m с кратностью 2l +1). Природа этого вырож-

дения связана со свойством центральной симметрии поля.

<<< < Предыдущая 1 2 3 4 5 67 / 207 8 9 10 11 12 13 14 15 16 17 18 19 20 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.04.2015501.2 Кб566решебник.docx
#
18.04.201513.95 Кб13россия.docx
#
11.07.201913.89 Mб14Рубинштейн С.Л. Основы общей психологии.rtf
#
22.08.201930.64 Кб5русский СЕЛЕЗНЁВА(ТРХ-111).docx
#
25.09.201969.55 Кб7с группы.docx
#
22.03.20162.6 Mб61с.м.чернов_квантовая механика.pdf
#
18.04.2015197.73 Кб38савицкая .docx
#
18.04.2015173.57 Кб13Сведения о родителях 2014-2015.doc
#
18.04.2015447.02 Кб13Сельский туризм.pdf
#
15.08.201956.85 Кб0сем1.docx
#
11.11.2019243.71 Кб9Семаго содер и организ.doc