Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Могилёвский государственный университет им. А. А. Кулешова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

с.м.чернов_квантовая механика

.pdf

Скачиваний:

Добавлен:

22.03.2016

Размер:

2.6 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 2016 17 18 19 20 > Следующая >>>

2.9. Доказать теорему:

Пусть имеется две физические величины F и R, самосопряженные операторы которых не коммутируют, так что выполняется условие:

[F, R] = i K .

Тогда утверждается, что неопределенности измерения величин связаны условием:

F R ≥ 1	K	.

2

F и R

(12.5)

Указание: Для доказательства рассмотреть интеграл вида:

I(α)=	∫		2


		αF- i R ψ	dV,

где α – произвольный вещественный параметр.

Решение:

Под неопределенностями физических величин F и R cледует понимать

среднеквадратичные отклонения F и R от своих средних значений:

F =

− <

R =

( F

;

( R − < R

>)2 .

Для нулевых средних значений

можно считать

< F

>=< R >= 0

F = F и

= R. Следует сразу отметить очевидное неравенство I (α)≥ 0 при любом α.

Используя свойство эрмитовости операторов

, не сложно преобразо-

и R

вать интеграл I (α)

к виду:

= ∫ψ

I (α)= ∫ α F −i R ψ

α F −i R

ψdV

α F +i R

α F −i R ψdV =

ψdV

=α2

= ψ α2 F

+iα

F R− R F

+ R

+α K +

≥ 0.

∫

Последнее неравенство при любом α имеет место, если дискриминант D

квадратного трехчлена не является положительным:

D =

− 4

≤ 0,

что и доказывает наше утверждение:

1 2

2 1 2

≥ 1

151

2.10. Показать, что в квантовой механике невозможно “измерить” две любые проекции момента импульса (например, Lx и Ly ). Однако,

квадрат момента импульса L2 может быть измерен вместе с любой своей проекцией (например, Lz ).

Решение:

Учитывая коммутационные соотношения между операторами проекций координаты и импульса (10.6), не сложно получить условия:

		= ihLz ;		2		= 0,
Lx	, Ly	= ihLz ;	Lz	, L		= 0,

которые и решают поставленную проблему.

2.11. Пусть оператор Q задан в виде двухрядной матрицы с известными матричными элементами aij :

	a	11	a	12
Q =					.
	a21		a22

Построить матрицу:

a) Единичного оператора I$.

b) Комплексно сопряженного оператора Q .

c) Транспонированного оператораQ .

d)Эрмитово сопряженного оператора Q .

-1

е) Обратного оператора Q .

+ -1

f) Унитарного оператора Q = Q .

Решение:

Воспользуемся общим правилом вычисления матричных элементов

оператора Q :

Qmn = ψm Qψn ,

атакже определениями соответствующих операторов, приведенных в таблице 1,

исвойствами скалярного произведения функций (10.10)-(10.12) и (11.12).

а) Imn =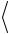ψm I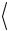$ψn =ψm ψn=δmn.

152

Результат:	$		1	0
Результат:	I	=	0	1	.
			0	1

b) Так как любое комплексное число имеет вид z = a + ib, то используя правило сложения матриц получаем:


Результат: Q	=	а11	а12	.
		а21	а22

ψm

= ψn

ψn

с)

Qmn =

Qψn

Qψm

Q ψm

Результат:

Q =

d) Воспользуемся результатом задачи (2.2): Q

	+
Результат: Q	=	а11	а21	.
		а12	а22



= Q		= Qnm .
	nm

= Q .

е) Для дальнейшего, введем определитель D =	а11	а12	= а а	22	− а а	21	, и
	а21	а22	11	22	12	21
	а21	а22

обозначим матричные элементы обратного оператора через xij . Запишем оп-

						−1	в развернутом виде:
ределение обратного оператора QQ						= I$	в развернутом виде:
	а	а	x	x	a x + a x		21	a x	+ a x			1	0
	11	12	11	12	= 11 11	12	21	11 12	12	22	=			.
	а21	а22	x21	x22	a21x11	+ a22 x21		a21x12	+ a22 x22			0	1

Приравнивая соответствующие матричные элементы, найдем искомые параметры:

x = a22 ;

x = − a12

;

x = −

a21

;

x =

a11

−1

a22

−a12

Результат: Q

a11

−a21

+ −1

f) На основании определения унитарного оператора Q

=Q и резуль-

татов п. d) и е), получаем:

a11

a21

a22

−a12

a11

a12

a22

−a21

Таким образом, окончательно имеем:

153

a	= Da	;
11	22					a22	−a21
a = −Da ;			Результат:			a22	−a21
12		21	Результат:	Q = D				.
a21 = −Da12 ;					−a12		a11
a	= Da .
22	11

2.12. Показать, что в квантовой механике имеют место те же соот-

ношения, что и в классической физике, но записанные для средних значений физических величин, в частности:

а)	d		< Px	>	(I теорема Эренфеста);
		< x >=
	dt	< x >=	m
	d
б)	d	< Px >=< Fx >= - < du				> (II теорема Эренфеста).
б)	dt	< Px >=< Fx >= - < du				> (II теорема Эренфеста).
	dt				dx

Решение:

Ограничимся одномерным движением частицы в поле U(x). Тогда опе-

ратор Гамильтона

имеет вид:

ˆ 2

(1)

+U (x)

а) рассмотрим вначале производную

dxˆ

∂ˆ

ˆ 2

xˆ,

+[xˆ

,U (x)]

xˆ

(2)

∂t

2mih

Используя известное коммутационное условие

ˆ 2

, путем его

x, Px

умножения на

слева и справа и последующего сложения, получаем:

ˆ 2

(3)

x, Px

2i Px .

Следовательно dxdtˆ = Pmx , и после усреднения получаем доказательство I теоремы Эренфеста:

< xˆ

d x

;

б) рассмотрим вначале производную

dPx

∂Px

ˆ ˆ

ˆ ˆ 2

∂t

P , H

, P

,U (x)	=	1	ˆ	,U (x)	.

		ih	P
			x

(4)

(5)

154

Подействуем коммутатором (5) на произвольную функцию ψ (x) , и уч-

тем, что Px = −ih

dψ (x)

dU (x)

Px,U (x) ψ

(x) = −ih

(U (x)ψ (x))+ihU (x)

= −ih

ψ (x).

В силу произвольности выбора ψ (x) , получаем полезное соотношение:

dU (x)

(6)

[Px ,U (x)] = −ih

F = − dU

Возвращаясь к уравнению (5) и вводя проекцию силы

, при-

ходим к условию II теоремы Эренфеста:

< Px >=< Fx >= − <

2.13. Будет ли сохраняться энергия E, импульс p , момент импульса L и L2 при свободном движении частицы?

Решение:

Для свободного движения частицы гамильтониан

	ˆ	2		ˆ 2	ˆ 2	ˆ 2
ˆ	ˆ			P	+ P	+ P
ˆ	P			x	y	z
H =			=				.		(1)
H =	2m		=		2m		.		(1)
	2m				2m				2
Элементарные расчеты показывают, что операторы									2
Элементарные расчеты показывают, что операторы								H ,p, L, L	коммути-

руют с операторами кинетической энергии (1), и не зависят явно от времени. Следовательно, все указанные параметры являются интегралами движения.

2.14. Какие из механических величин E, p, L, L сохраняются при

движении частицы в поле вида:

а) u(z) = a0z ;

б) u(z,t) = a(t)z .

Решение:

Гамильтониан частицы равен:

			ˆ 2
		ˆ	P
		H =	2m	+u .	∂H	(1)
			2m
Очевидно, Е=const в случае (а), однако E=E(t) в случае (б) т.к.						≠ 0 .
					∂t	≠ 0 .
	ˆ2				∂t
Все операторы p , L и	ˆ2	явно от времени не зависят и коммутируют с
Все операторы p , L и	L	явно от времени не зависят и коммутируют с

операторами кинетической энергии, поэтому осталось рассмотреть коммутаторы этих операторов с операторами потенциальной энергии. При этом можно не разделять случаи (а) и (б).

155

= −ih

∂u

= 0

Px = const.

∂x

= −ih

∂u

= 0

= const.

∂y

= −ih

∂u

= −iha ≠ 0 Pz ≠ const.

∂z

Lx,u

yPˆ z

− zPˆ y , u

= y Pz , u

= −ihya ≠ 0 Lx ≠ const.

Ly,u

zPˆ x

− xPˆ z ,u

= −x Pz , u

= ihya ≠ 0 Ly ≠ const.

= 0

Lz,u

xPˆ y − yPˆ x , u

Lz = const.

ˆ2

≠ const.

+ L y

+ Lz ,u

≠ 0 L

Ответ: E=const в случае (а).

Востальных случаях сохраняются Px , Py , Lz .

2.15.В каких силовых полях U(r) проекция момента импульса Lz

будет интегралом движения?

Решение:

Для положительного ответа на этот вопрос достаточно выполнения условия:

= x

− y

∂u

− y

∂u

= 0 .

(1)

Lz,u

xPˆ y − yPˆ x , u

Py , u

Px , u

= −ih x

∂y

∂x

Соотношение (1) выполняется в двух случаях:

1.∂∂ux = ∂∂uy = 0 и следовательно поле u=u(z) обладает цилиндрической сим-

метрией относительно вращения вокруг оси Z.

2. Поле является центрально-симметричным, u=u(r) где r = x2 + y2 + z2 .

Действительно: ∂u∂(yr) = ry ∂∂ur ; и следовательно Lˆz , u(r) = 0 .

Ответ: u=u(r); u=u(z).

156

Задачи к главе III

3.1. Частица с массой m движется в одномерном поле U(x) вида:

∞,		x ≤0	(областьI);

U(x) = 0, 0 < x ≤a(областьII);				(1)
				(1)
U0	,	x > a	(областьIII).

а) Показать, что для E > U0 частица имеет непрерывный спектр

энергии.

б) Получить уравнение, определяющее спектр энергии E в случае

E < U0 .

в) Считая m и a известными, определить минимальное значение U0 , при котором появляется первый дискретный энергетический уро-

вень. Какова его энергия?

г) При каком минимальном U0 внутри ямы появляется n-й энерге-

тический уровень? Сколько дискретных уровней в яме, если U0 = 8 π2h2 ?

mа2

Решение:

а) Решение УШ в указанных трех областях имеют вид:

ψ1(x) =0

ψ2 (x) = Asin(k2 x +α2 ) ,

ψ3 (x) = Bsin(k3x +α3 )

где k2 =	2mE2 , k3 =	2m2 (E −U0 )
	h	h

“Стандартные условия” сводятся к граничным условиям:

(2)

(3)

ψ1 (0) =ψ2 (0) = 0 , ψ2 (a) =ψ3 (a) , ψ2' (a) =ψ3'

(a) ,

(4)

которые приводят к условию α2	= 0 и уравнению на собственные значения E,
входящая в k2 и k3 (3):
	k2ctgk2a=k3ctg(k3a+α3).				(5)
Так как в уравнении (5) параметр α3 является произвольным действи-
тельным числом, то и энергия E >U0		может принимать любые значения в за-
висимости от начальных условий задачи.
б) При E <U0 параметр k3	(3) является чисто мнимым k3 = iχ , где
	χ =		2m	(U0 − E) ,	(6)

			h2
		157

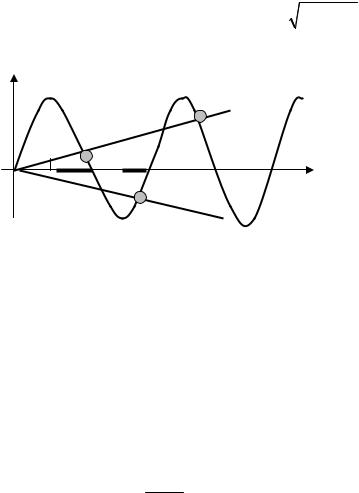
так что решение УШ в области III (x>a) принимает вид:

ψ3 (x) = Be−χx +ceχx .

(7)

Для выполнения условия ограниченности волновой функции (7) следу-

ет положить c=0, и граничное условие (4) приводит к уравнению:

tgk2a = −

(8)

Очевидно, решение последнего уравнения существует, если tgk2 a < 0 .

Учитывая соотношение sin k2a =

tg2k

, уравнение (8) можно привести к ви-

+ tg2k2a

ду:

sin k2a = ±k2

(9)

2mU0a2

Графическое решение последнего уравнения представлено на рисунке для случая трех дискретных уровней в яме.

					Рис. 14. Графическое решение
	π		3π		уравнения (9)
0	π	π	3π	2π	k2a
	2		2

в) Первый дискретный уровень появляется при условии k2 a = π2 , что соответствует энергии:

E1 =	h2k22		π 2h2
		=		.	(10)
	2m		8ma2

Из уравнения (9) получается минимальная высота потенциальной ступеньки U0 , равные U0 = E1 .

г) U0 = (2n −1) π2h2 , 4 уровня энергии.

8ma2

3.2. Найти уровни энергии и волновые функции линейного гармонического осциллятора, помещенного в постоянное однородное электрическое поленапряженностью ε, направленноевдольосиx. Зарядчастицы равен e .

158

Решение:

Осциллятор, находящийся в электрическом поле ε , обладает потенциальной энергией вида:

	mω2 x2		mω2 x2			e2ε2
U (x) =		−eεx =		1	−		,
	2		2			2mω2

где введено обозначение:

x1 = x − meωε 2 .

С учетом условия (2), УШ осциллятора имеет вид:

−	h2	d 2ψ (x1 )	+	mω2 x12	ψ (x ) = Eψ (x ) ,
	2m dx2
			2		1	1	1
1

E1 = E + e2εω22 .

(1)

(2)

(3)

)

Тогда, для уровней энергии и волновой функции осциллятора в электрическом поле ε . Окончательно получаем:

E		= hω(n +	1	) −	e2ε2		, n = 0,1, 2K	(5)
	n		2		2mω	2

−1 x12

ψn = Ane 2 a2 Hn x1 . (6)a

Заметим, что частота излучения осциллятора ω1 при включении одно-

родного электрического поля не изменяется ω1 =ω .

3.3. Найти уровни энергии и волновые функции трехмерного гармонического осциллятора с потенциальной энергией вида:

U(x, y, z) =	mω12x2	+	mω22y2	+	mω32z2	(1)
	2		2		2

Рассмотреть случай изотропного осциллятора ω1 = ω2 = ω3 = ω0 .

Решение:

Динамика движения частицы описывается трехмерным стационарным УШ вида:

−	h2	ψ (x, y, z) +U (x, y, z)ψ (x, y, z) = Eψ (x, y, z) ,	(2)
	2m

где оператор Лапласа

= ∂2 + ∂2 + ∂2 ∂x2 ∂y2 ∂z2

159

В случае потенциала (1) переменные в уравнении (2) можно разделить, подставив волновую функцию в виде:

ψ(x, y, z) =ψ1 (x)ψ2 ( y)ψ3 (z)

При этом для каждой i-ой координаты получается обыкновенное диф-

ференциальное уравнение для линейного гармонического осциллятора с энергиями:

Ei	= hωi (ni	+	1	),	ni =0,1, 2K.
			2

Тогда полная волновая функция осциллятора и энергия имеют вид:

−

(

)

n1,n2

(x, y, z) = Ae

3 H

(

) ,

(5)

,n3

где a =

mωi

E = E1 + E2 + E3 = hω1 (n1 +

) + hω2 (n2

)

+ hω3 (n3

) .

(6)

В случае изотропного осциллятора, когда ω1 =ω2 =ω3 =ω0 , уровни энер-

гии En равны:

= hω0 (n +

(7)

где n = n1 +n2 +n3 = 0,1, 2K

В последнем случае, в силу центральной симметрии задачи уровни

энергии вырождены с кратностью вырождения k =

(n +1)(n + 2) .

3.4. Осциллятор находится в основном состоянии с нормированной

волновой функцией вида:

ψ(x)=

e-2a

, где a =

mω .

4 π

Найти вероятность его пребывания вне классических границ поля.

Решение:

Классические границы области движения осциллятора найдем из условия U (x0 ) = E , т.е.

mω2 x2

hω;

(1)

= ±

mω

Найдем вначале вероятность w1

нахождения осциллятора в классически

разрешенной области движения (−x0 ≤ x ≤ x0 ):

160

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 2016 17 18 19 20 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.04.2015501.2 Кб566решебник.docx
#
18.04.201513.95 Кб13россия.docx
#
11.07.201913.89 Mб14Рубинштейн С.Л. Основы общей психологии.rtf
#
22.08.201930.64 Кб5русский СЕЛЕЗНЁВА(ТРХ-111).docx
#
25.09.201969.55 Кб7с группы.docx
#
22.03.20162.6 Mб61с.м.чернов_квантовая механика.pdf
#
18.04.2015197.73 Кб38савицкая .docx
#
18.04.2015173.57 Кб13Сведения о родителях 2014-2015.doc
#
18.04.2015447.02 Кб13Сельский туризм.pdf
#
15.08.201956.85 Кб0сем1.docx
#
11.11.2019243.71 Кб9Семаго содер и организ.doc