
с.м.чернов_квантовая механика
.pdfОднако функция ψ1(q1q2 ) не обладает требуемым свойством симметрии,
и, следовательно, не может описывать тождественные частицы. Непосредственно подстановкой легко убедиться, что той же энергией
обладает система двух частиц с волновой функцией:
ψ2 (q1q2 ) =ψn1 (q2 )ψn2 (q1) .
|
|
|
|
|
|
Hψ2 |
= (H1 |
+ H 2 )ψn1 (q2 )ψn2 (q1) =ψn1 (q2 ) H1ψn2 (q1) +ψn2 (q1 ) H2 |
ψn1 (q2 ) = |
||
=(En2 + En1 )ψ2 = Eψ2.
Всилу линейности уравнения Шредингера, любая линейная комбина-
ция ψ1 и ψ2 также удовлетворяют уравнению Шредингера с той же энергией
E .
ψ(q1q2 ) = c1ψ1(q1q2 ) + c2ψ2 (q1q2 ) .
Вчастности, чтобы функция ψ была симметричной (бозоны) можно
выбрать c1 = c2 , т.е.
ψs (q1q2 ) = c1(ψn1 (q1)ψn2 (q2 ) +ψn1 (q2 )ψn2 (q1)) .
Для антисимметричной волновой функции (фермионы) положим c2 = −c1 :
ψа(q1q2 ) = c1(ψn1 (q1)ψn2 (q2 ) −ψn1 (q2 )ψn2 (q1)) .
Для системы из N частиц легко получить симметричную и антисимметричную функции, выраженные через одночастичные волновые функции. В частности, для фермионов удобно записать волновую функцию в виде определителя:
|
|
ψn (q1) |
ψn (q2 )..... |
ψn (qN ) |
|
|||
|
|
|
1 |
|
1 |
|
1 |
|
ψа |
= c1 |
ψn (q1) |
ψn (q2 )..... |
ψn (qN ) |
. |
|||
|
|
|
2 |
|
2 |
|
2 |
|
|
|
ψn |
(q1) |
ψn |
(q2 )..... |
ψn |
(qN ) |
|
|
|
|
N |
|
N |
|
N |
|
При перестановке q1 ↔ q2 переставляются 1-ый и 2-ой столбцы и определи-
тель меняет знак.
Предположим, что в системе тождественных фермионов два квантовых состояния совпадают n1 = n2 , или, иными словами, система содержит
фермионы в одинаковых квантовых состояниях. Тогда две строки определителя тождественны и ψа = 0 . Следовательно, такое состояние становится не-
возможным. Отсюда возникает важный принцип (принцип запрета Паули). В определенном квантовом состоянии не может находиться более одного фермиона. Данный принцип не применим к бозонам.
Для атомов можно дать частную формулировку принципа Паули: в
атоме не может быть более одного электрона с одинаковыми наборами из 4-х квантовых чисел n,l,me ,ms .
101
§ 40. Основное состояние гелиоподобных атомов
Атом гелия, второй химический элемент периодической системы и является наиболее простым из многоэлектронных атомов. Однако уже на нем классическая теория, как и полуклассическая теория Н. Бора, потерпела полный крах. Только квантовая механика смогла правильно описать структуру энергетического спектра и наблюдаемые серии линий излучения атома гелия.
Вообще говоря, атом гелия представляет собой задачу о движении трех взаимодействующих частиц. Задача этого класса не может быть решена точно, поэтому для количественных оценок будем использовать стационарную теорию возмущения.
Рассмотрим структуру волновой функции двухэлектронной системы. Из принципа тождественности следует, что волновая функция фермионов, зависящая от пространственных (r) и спиновых (ms) переменных должна быть
антисимметрична относительно перестановки двух электронов.
ψa =ψ (r1,ms1;r2 ,ms2 )= −ψ (r2 ,ms2;r1,ms1 ).
Если координатная и спиновая переменная являются независимыми, что имеет место при отсутствии спин-орбитальных сил, то волновая функция может быть представлена в виде произведения координатной функции
Φ(r1 ,r2 ) на спиновую ϕ(ms1,ms2 ):
ψ(r1,ms1;r2 ,ms2 ) = Φ(r1 ,r2 )ϕ(ms1,ms2 ).
При чtм здесь имеется две возможности для симметрии (s) или антисимметрии (a) функций относительно своих аргументов:
ψa(1) =Φaϕs;
ψa(2) =Φsϕa.
Можно строго доказать (задача 3.17), что эти волновые функции описывают систему двух электронов с квантовыми числами полного спина s =1 и s = 0 , соответственно.
Этот результат позволяет в дальнейших расчетах вообще игнорировать зависимость от спиновых переменных в волновой функции. При этом необходимо учитывать тот факт, что если полученная координатная волновая функция является антисимметричной, т.е. Φ = Φa (r1 ,r2 ), то ей соответствует
симметричная спиновая функция ϕs (ms1,ms2 ) и спин двухэлектронной сис-
темы s = 1. В противном случае, для симметричной координатной функции
Φs (r1 ,r2 ), спин системы s = 0.
Считая ядро атома гелия неподвижным, и, пренебрегая несущественными поправками на спин-орбитальные взаимодействия, гамильтониан гелиоподобного атома можно представить в виде:
102

|
|
|
h |
2 |
|
|
|
|
Ze |
2 |
|
h |
2 |
|
|
Ze |
2 |
|
|
e |
2 |
|
|||
|
H = − |
|
|
|
− |
|
− |
|
|
− |
|
|
|
+ |
|
|
= |
||||||||
|
2m |
1 |
4πε |
r |
2m |
2 |
4πε |
0 |
r |
4πε |
r |
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
-e r12 = r2 −r1 |
-e |
|
|
0 |
|
|
|
|
0 1 |
|
|
0 |
|
|
|
|
2 |
|
|
|
0 12 |
|
|||
|
|
|
|
|
|
′. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
= |
H 1 + H 2 |
+ H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
r1 |
r2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ze |
Координатная |
|
часть |
|
|
волновой |
|
|
функции |
||||||||||||||||
|
Φ(r1 ,r2 )находится как решение стационарного УШ: |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(40.1) |
|
|
|
|
|
|
|
|
|
|
H Φ = EΦ. |
|
|
|
|
|
|
|
|
|
|
||||||
Из-за наличия взаимодействия между электронами переменные в уравнении (40.1) не разделяются, и задача не может быть решена точно. Поэтому энергию основного (невырожденного) состояния будем оценивать с помощью
стационарной теории возмущения. При этом будем считать H′ оператором
возмущения и «малым» по сравнению с H 0 = H1 + H 2 .
В нулевом приближении H ′= 0 атом гелия представляет собой сово-
купность двух независимых водородоподобных атомов, описываемых УШ вида:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= E0Φ0 . |
|
|
|
|
|
|
(40.2) |
||||||||||
|
|
|
|
|
|
|
|
|
H 0 Φ0 |
|
|
|
|
|
|
|||||||||||||||||
При этом для основного состояния (n =1, l = 0, m = 0) имеем: |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
E0 = E1 + E2 = 2E1; |
|
|
|
|
|
(40.3) |
||||||||||||||||||
|
|
|
|
|
|
Φ0 =ψ100 (r1 )ψ100 (r2 ); |
|
|
|
|
|
|||||||||||||||||||||
где |
|
E1 = − |
|
|
m e4 |
2h2 Z |
2 |
= −13,6 Z |
2 |
эВ, |
|
|
(40.4) |
|||||||||||||||||||
|
(4πε0 )2 |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
3 2 |
|
− |
Z |
r |
|
|
|
|
|
|
||||||
|
|
|
ψ100 (r )= |
|
|
Z |
|
|
e |
ao |
|
≡ψ1 (r ), |
|
|
(40.5) |
|||||||||||||||||
|
|
|
π |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
(4πε |
|
)h |
|
|
|
|
|
a0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
a |
= |
|
0 |
2 |
= 0,528 10−10 |
м – 1-й боровский радиус. |
|
|||||||||||||||||||||||||
|
m e2 |
|
|
|||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, в нулевом приближении энергия и волновая функция |
||||||||||||||||||||||||||||||||
основного состояния атома гелия равны соответственно: |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
E0 = 2E1 = − |
|
m e4 |
|
|
|
|
|
2 |
|
= −27,2 Z |
2 |
эВ |
(40.6) |
||||||||||||||||
|
|
|
(4πε0 )2 h2 Z |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
3 |
|
− |
Z |
(r |
+r |
) |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
Φ |
|
(r ,r )= |
|
|
|
e ao |
1 |
2 . |
|
|
(40.7) |
||||||||||||||||
|
|
|
|
|
|
πa3 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Заметим, что координатная волновая функция Φ0 = Φs (r1,r2 ) |
симмет- |
|||||||||||||||||||||||||||||||
рична, следовательно, спин основного состояния атома гелия s = 0. Этот результат согласуется и с принципом Паули, так как оба электрона, хотя имеют
103
одинаковые наборы квантовых чисел (n,l,m)= (1,0,0), находятся в различных
спиновых состояниях ms = ± 1/2.
Для решения задачи в первом приближении будем считать оператор
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
возмущения H ′ ≠ 0 . Тогда по теории возмущения первая поправка к энергии |
||||||||||||||||||||||||
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
E |
равна среднему значению оператора H ′= 4πε r , взятому по невозмущен- |
|||||||||||||||||||||||
|
||||||||||||||||||||||||
ным волновым функциям Φ0 |
|
(40.7): |
|
|
|
|
|
|
|
|
|
0 12 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
′ |
|
|
|
(r ,r ) |
|
e2 |
|
|
(r ,r )dVdV . |
|
||||||||||||
|
|
E = |
∫ |
Φ |
|
|
|
|
Φ |
|
||||||||||||||
|
|
4πε r |
|
|
||||||||||||||||||||
|
|
|
|
0 1 2 |
|
0 1 2 |
|
|
1 |
2 |
|
|
||||||||||||
Запишем последний интеграл в виде: |
|
0 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
dV ψ |
2 (r )(−e) |
|
|||||||||||||||||||
|
|
E′ = ∫dV1ψ12 (r1 )( |
−e)∫ |
. |
||||||||||||||||||||
|
|
|
2 1 |
|
|
2 |
|
|
|
|||||||||||||||
|
|
|
(4πε |
0 |
)r |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Внутренний интеграл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|||||
|
|
|
|
dV2ψ12 (r2 )(−e) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
ϕ(r )= |
∫ |
|
= |
∫ |
|
|
dQ |
|
||||||||||||||
|
|
|
(4πε |
|
)r |
|
|
(4πε |
|
)r |
|
|||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|||||||||
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
12 |
|
|
|||
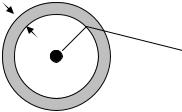
имеет вполне определённый физический смысл: он представляет собой элек-
тростатический потенциал, создаваемый в точке r1 вторым электронным облаком.
dr2 |
dV2 |
Учитывая центральную |
симметрию |
|||
задачи, разобьем объем атома на тонкие |
||||||
rr |
r12 dV1 |
|||||
сферические слои радиуса r |
и толщиной |
|||||
|
|
|
|
2 |
|
|
|
|
r1 |
|
dr2 , в которых сосредоточен электрический |
||
|
|
|
||||
|
|
|
|
заряд. |
|
|
dQ = −eψ12 (r2 )4πr22dr2
Из электродинамики известно, что потенциал внутри заряженной сферы постоянен и равен потенциалу на сфере, а вне неё он равен потенциалу точечного заряда, сконцентрированного в центре сферы, т.е.:
|
dQ |
, |
r ≤ r ; |
|||
|
4πε r |
|||||
|
|
2 1 |
||||
|
0 1 |
|
|
|
||
dϕ = |
dQ |
|
|
|
||
|
|
|
, |
r2 ≥ r1. |
||
|
|
|
||||
|
4πε0r2 |
|
|
|
||
|
|
|
|
|||
Тогда внутренний интеграл можно записать в виде:
|
|
|
|
|
|
|
|
r1 |
|
|
|
|
|
|
|
|
∞ |
( |
−e ψ |
2 |
|
r |
2 |
dr |
|
|||
ϕ(r )= |
|
|
1 |
|
∫ |
(−e)ψ 2 |
(r |
)4πr2dr + |
∫ |
|
) |
|
1 |
( 2 ) |
2 2 |
= |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
1 |
|
|
|
|
|
|
|
1 |
2 |
|
|
2 |
2 |
|
|
|
|
4πε0r2 |
|
|
|||||||
|
|
|
4πε0r1 0 |
|
|
|
|
|
|
|
|
r1 |
|
|
|
|
|
|
||||||||||
|
|
4e |
|
|
|
Z |
|
3 |
r |
|
−2 |
Z |
r |
∞ |
|
|
|
−2 |
Z |
r |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
= − |
|
|
|
|
|
|
|
1 |
∫dr2r22e |
|
ao |
|
+ ∫ dr2r2e |
|
ao |
|
. |
|
|
|
||||||||
|
4πε |
|
|
a |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
0 |
|
|
|
|
r |
0 |
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
0 |
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
104

Интегралы в квадратных скобках легко вычисляются по частям:
∫dxxeax = |
|
e ax |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
x − |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2 |
|
ax |
|
|
|
|
|
e ax |
|
2 |
|
|
|
x |
|
2 |
|
|
|
|
|
||||||||
∫dxx |
e |
|
|
= |
|
|
|
|
x |
|
− |
2 |
|
|
+ |
|
|
|
|
|
. |
|
|
|||||||
|
|
a |
|
a |
|
a |
2 |
|
|
|
||||||||||||||||||||
Тогда для потенциала ϕ(r1 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
e |
|
|
|
Z |
|
|
|
a |
|
|
|
|
|
|
a |
|
|
|
−2 |
Z |
r |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
||||||||||||||||
ϕ(r )= − |
|
|
|
|
|
|
|
− |
1 |
+ |
|
e |
|
|
1 |
. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
0 |
|
||||||||||
4πε |
|
|
a |
|
|
|
|
Zr |
|
|
|
|
||||||||||||||||||
1 |
|
|
|
|
Zr |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
0 |
|
|
0 |
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставляя ϕ(r1 ) в выражение для E′, окончательно получаем:
E′ = ∫dV1ψ |
2 |
(r1 )(−e)ϕ(r1 )= |
5 m e4 |
|
Z. |
||
1 |
|
0 |
2 |
|
|||
|
|
|
|
|
|
||
|
|
|
8 |
(4πε0 ) |
|
h2 |
|
При вычислениях мы воспользовались интегралами, которые так же легко получаются с помощью процедуры интегрирования по частям, вида:
∞∫dxxne−ax = ann+!1 .
0
Следовательно, энергия нормального состояния атома гелия в первом приближении теории возмущения равна
E = E0 |
+ E′ = − |
m e4 |
|
|
2 |
− |
5 |
|
|
2 |
− |
5 |
|
(40.8) |
0 |
2 Z |
|
8 |
Z = −27,2 |
Z |
|
8 |
Z (эВ). |
||||||
|
|
h2 (4πε0 ) |
|
|
|
|
|
|
|
|
|
|
||
Полученный результат справедлив не только для атома гелия, но и для |
||||||||||||||
других двухэлектронных атомных |
|
систем, таких |
как |
|
Li+, Be++, B+++,C++++ |
|||||||||
и т.д. Сравнение расчётных и экспериментальных результатов удобно представить в виде следующей таблицы:
|
|
Нулевое |
Первое |
|
|
|
|
|
|
Атом |
−Eэксп. |
прибли- |
δ0 |
= Еэксп. |
− Е0 |
|
|
||
приближение |
δ1 |
= Еэксп. − Е |
|||||||
(ион) |
(эВ) |
жение |
|
|
|
||||
−Е0 (эВ) |
|
|
|
|
|
||||
|
|
−(Е0 + Е′) |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
He |
78,6 |
108,8 |
74,8 |
|
30,2 |
|
|
-3,8 |
|
Li+ |
197,1 |
244,8 |
193,8 |
|
47,7 |
|
|
-3,30 |
|
Be++ |
370,0 |
435,2 |
367,2 |
|
65,2 |
|
|
-2,8 |
|
B+++ |
596,4 |
680,0 |
595,0 |
|
83,6 |
|
|
-1,4 |
|
C++++ |
876,2 |
979,2 |
877,2 |
|
103,0 |
|
|
1,0 |
Из таблицы видно, что абсолютная ошибка первого приближения δ1 остаётся практически постоянной и составляет 1+4эВ. Так как величина иони-
105
зационного потенциала возрастает с ростом Z , то относительная ошибка убывает: для He она составляет 4,8%, а для C++++ она падает до 0,1%. В целом
полученные результаты можно считать удовлетворительными, если учесть,
что H ′ не является исчезающее малым, и не следовало ожидать хороших результатов при использовании теории возмущения в линейном приближении.
§ 41. Возбужденные состояния атома гелия. Орто- и парагелий. Обменная энергия
В предыдущем параграфе рассмотрено нормальное состояние атома гелия, когда электроны находились в основном состоянии водородоподобного атома. Рассмотрим теперь случай, когда электроны могут находиться в любых состояниях с волновой функцией ψn (r ), где индексом (n) обозначен пол-
ный набор квантовых чисел (n,1,m).
Как уже отмечалось, полный гамильтониан атома гелия в системе координат, связанной с неподвижным ядром, имеет вид:
|
ˆ |
ˆ |
|
|
|
ˆ |
|
ˆ |
' |
|
|
ˆ |
|
ˆ ' |
, |
||
|
H |
= H1 |
+ H2 |
+ H |
|
= H0 |
+ H |
||||||||||
где: |
|
|
h |
2 |
|
|
|
2e |
2 |
|
|
|
|
|
|||
H i |
= − |
|
|
i |
− |
|
|
|
, |
(i =1, 2), |
|||||||
2m |
|
4πε |
0 |
r |
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
i |
|
|
|
||
|
|
|
|
|
e |
2 |
– “малый” оператор возмущения. |
||||||||||
|
H ′ = |
|
|
|
|
||||||||||||
|
4πε |
|
r |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
0 12 |
|
|
|
|
|
|
|
|
|
|
|
Дальнейший анализ будем проводить также в рамках стационарной теории возмущения. Для этого еще раз опишем “нулевое” приближение, ко-
гда ˆ ' = . Движение электронов описывается стационарным УШ:
H 0
|
|
(41.1) |
(H1 + H 2 )Ф0 (r1,r2 ) = E0Ф0 (r1,r2 ) . |
||
Решение уравнения (41.1) распадается на две водородоподобные зада- |
||
чи, волновые функции и энергия которых имеет вид: |
(41.2) |
|
Ф0 (r1,r2 ) =ψ1(r1)ψ2 (r2 ) ≡Ф1(r1,r2 ) , |
||
|
E0 = En1 + En2 . |
|
При этом движение каждого электрона описывается одночастичным |
||
УШ: |
|
|
ˆ |
(ri ) = Eniψi (ri ), (i =1, 2) . |
(41.3) |
Hiψi |
||
Однако, в силу тождественности электронов, той же E0 энергии соот-
ветствует и другая волновая функция с переставленными координатами электронов:
Ф0 (r1,r2 ) =ψ1(r2 )ψ2 (r1) ≡Ф2 (r1,r2 ) . |
(41.4) |
106
Решением векового уравнения (41.10) являются поправки E1,2' = K ± A. Та-
|
|
|
|
ˆ |
' |
приводит к расщеплению |
||
ким образом, наличие оператора возмущения H |
|
|
||||||
двукратно вырожденного уровня E0 |
на два подуровня: |
|
||||||
E = E + E' |
|
= E + K + A ≡ E |
s |
|
(41.11) |
|||
0 |
1 |
|
|
0 |
|
|||
|
|
|
|
|||||
E = E |
+ E' |
|
= E + K − A ≡ E |
a |
|
|
||
0 |
2 |
|
0 |
|
|
|
||
где: |
E0 = En1 + En2 . |
|
|
|
|
|||
Найдем далее коэффициенты c1 |
и c2 , и следовательно волновые функции |
|||||||
в нулевом приближении, соответствующие найденным значениям энергии. Для этого подставим последовательно в систему уравнений (41.7) корни векового уравнения (41.10). При E = Es ( E' = K + A) для волновой функции име-
ем:
Φ ≡ Φs = c1 (Φ1 +Φ2 ) ,
где c1 легко найти из условия нормировки для Ф с учетом ортонормированности Φi :
∫Φ*i Φk dV1dV2 = δik ,
что дает c1 = 12 . Окончательно для состояния с энергией Es мы получаем волновую функцию вида:
Φ |
s |
= |
1 |
(ψ |
(r )ψ |
|
(r |
) +ψ |
(r )ψ |
|
(r )) . |
(41.12) |
|
2 |
2 |
||||||||||
|
|
2 |
1 |
1 |
2 |
1 |
2 |
1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Аналогично, для энергии E = Ea ( E' = K − A ) имеем:
Φ |
a |
= |
1 |
(ψ |
(r )ψ |
|
(r |
) −ψ |
(r )ψ |
|
(r )) . |
(41.13) |
|
2 |
2 |
||||||||||
|
|
2 |
1 |
1 |
2 |
1 |
2 |
1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Из приведенных расчетов видно, что энергии Es соответствует симметричная координатная волновая функция Φs , которой отвечает в свою очередь антисимметричная спиновая – ϕa , описывающая синглетное спино-
вое состояние s = 0 с единственной проекцией спина системы. Напротив, энергии Ea соответствует антисимметричная координатная функция Φa , и,
следовательно, симметричная спиновая – ϕs , что соответствует триплетному
спиновому состоянию s = 1 ( ms = 0, ±1). Состояние атома гелия с s = 0 называ-
ется парасостоянием или парагелием, а с s = 1 – ортогелием. Из-за слабого спин – спинового взаимодействия, которым мы вообще пренебрегаем, пере-
ходы с переворачиванием спина маловероятны. Следовательно, в природе существует как бы два сорта атомов гелия, имеющие свои независимые наборы энергетических уровней (рис. 14).
108
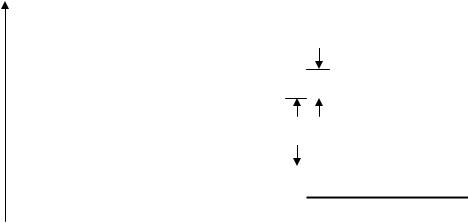
E |
|
|
|
E0=E1+E2 |
E1+E2+K+A |
|
E1+E2+K - A |
|
|
2А |
|
|
|
||
|
|
|
|
|
20эВ |
||
Е0=Е1+Е1 |
E1+E1+K+A |
|
|
|
|
E1+E1+K - A |
|
|
|
|
|
HÈ=0, S=0. |
H ′ ≠ 0, S = 0. |
(запрещенный уровень) |
|
|
H ′ ≠ 0, S =1. |
||
(парагелий) |
(парагелий) |
|
(ортогелий) |
Рис. 14. Энергетические уровни атома гелия
Заметим, что уровня E1 +E1 +К− А для ортогелия не существует. В противном случае мы имели бы два электрона в одинаковых квантовых состоя-
ниях: ( n,1, m1, ms )=(1,0,0, 12 ), что противоречит принципу запрета Паули. По-
этому основным состоянием атома гелия является парагелий. Ортосостояния можно получить искусственно, например, путем соударения электронных пучков с атомами гелия или передачи электронов от одних атомов к другим при газовых разрядах.
Так как время жизни ортогелия резко возрастает, достигая величины10−3 c, то таким образом можно накапливать атомы в возбужденных, метастабильных состояниях. Это явление широко используется при создании га-
зовых лазеров.
Выясним физический смысл параметров К и А, которые в конечном счете определяют специфическую структуру энергетических уровней атома гелия. В соответствии с соотношениями (41.8) и (41.9) имеем:
|
(−e) |
|
ψ |
(r ) |
|
2 |
(−e) |
|
ψ |
|
(r ) |
|
2 |
|
|||||||||||
|
|
|
|
|
|||||||||||||||||||||
K = H11' = H22' = ∫ |
|
|
|
1 |
1 |
|
|
|
|
|
|
2 |
2 |
|
|
|
dV1dV2 . |
||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
4πε0r12 |
|
|
|
|
|
||||||||||||
Очевидно выражения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
ρ (r ) = −e |
|
ψ |
|
(r ) |
|
|
|
|
|
|
|
(41.14) |
|||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
1 |
1 |
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||
ρ |
(r ) = −e |
|
ψ |
2 |
(r ) |
|
2 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
2 |
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
представляют собой плотности электрических зарядов электронов, находя-
щихся в 1-м и 2-м квантовых состояниях. Следовательно, физически параметр
K = ∫ |
ρ1 (r1 )ρ2 |
(r2 ) |
dV1dV2 |
(41.15) |
4πε r |
|
|||
|
0 12 |
|
|
|
|
109 |
|
|
|
представляет собой кулоновскую энергию электростатического взаимодей-
ствия двух электронных облаков, “размазанных” в пространстве с плотностями ρ1 и ρ2 .
Однако, столь наглядную интерпретацию параметру А дать невозмож-
но.
|
|
|
|
* |
|
|
|
* |
|
|
A = H12' = H |
21' = ∫ |
(−e)ψ1 |
(r1 )ψ2 (r1 ) (−e)ψ1 (r2 )ψ2 |
(r2 ) |
dV1dV2 . |
|||||
|
|
4πε0r12 |
|
|||||||
Введем обозначения: |
|
|
|
|
|
|
|
|||
|
ρ (r ) = −eψ* (r )ψ (r ); |
|
|
|||||||
|
|
(41.16) |
||||||||
|
12 |
1 |
1 |
1 |
2 |
1 |
||||
|
|
|
||||||||
|
|
ρ |
21 |
(r ) = −eψ* (r )ψ |
(r ). |
|
|
|||
|
|
|
2 |
2 |
2 |
1 |
2 |
|
|
|
Эти параметры можно рассматривать формально как плотности зарядов, вычисленные для таких состояний, когда каждый электрон одновременно находится как в первом, так и во втором квантовом состоянии. Эти величи-
ны могут быть и комплексными, и, следовательно, термин “плотность заряда” следует употреблять весьма условно. Их иногда называют обменными плот-
ностями зарядов. Поэтому энергия А:
A = ∫ |
ρ12 (r1)ρ21 |
(r2 ) |
dV1dV2 |
(41.17) |
4πε r |
|
|||
|
0 12 |
|
|
|
также называемая обменной энергией, не поддается наглядному (классиче-
скому) истолкованию. Название это происходит от того, что для наглядности считают, что между электронами помимо кулоновского взаимодействия
(41.15) возникают дополнительные обменные силы, связанные с тем, что электроны постоянно обмениваются квантовыми состояниями.
На самом деле смысл обменного интеграла А совершенно иной. Согласно теории возмущения линейная поправка к энергии равна среднему значению возмущения, усредненному по невозмущенным волновым функциям. В нашем случае возмущением является кулоновская потенциальная энергия, а невозмущенные волновые функции удовлетворяют принципу тождественно-
сти, приводящие к появлению симметричных или антисимметричных координатных волновых функций. Возьмем, к примеру, симметричную коорди-
натную волновую функцию Φs (41.12), описывающую парагелий. Тогда средняя кулоновская энергия будет равна:
s |
* |
e2 |
1 |
|
dV dV |
|
|
|
|
|
|
1 |
2 |
|
|
|
|||
Ek |
= ∫Φs |
4πε r |
ΦsdV1dV2 = 2 |
∫ |
4πε r |
|
(ρ1 |
(r1)ρ2 |
(r2 ) + ρ1(r2 )ρ2 (r1) + ρ12 (r1)ρ21(r2 ) + ρ21(r1)ρ12 (r2 )). |
|
|
0 12 |
|
0 12 |
|
|
|
||
Очевидно, как и раньше, первые два интеграла, так же как и два последних равны между собой. Поэтому, сокращая на два, и используя обозначения (41.15) и (41.17) для кулоновской и обменной энергии, получаем:
Eks = K + A.
110
