Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Могилёвский государственный университет им. А. А. Кулешова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

с.м.чернов_квантовая механика

.pdf

Скачиваний:

Добавлен:

22.03.2016

Размер:

2.6 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1718 / 2018 19 20 > Следующая >>>

3.16. Найти результат действия операторов σ$x , σ$y , σ$z на базовые спи-

новые функции:

		1	;		0
	α =	0	;	β =	1	.
		0			1
Ответ: σ x α = β;	σ y α = iβ; σ z α =α;
σ x β =α;	σ y β = −iα;	σ z β = −β.

3.17. Показать, что в системе из двух электронов спиновые функции φs,ms , соответствующие значению полного спина s = 1, описываются

симметричными функциями, а в случае s = 0 – антисимметричными функциями вида:

	s = 0	φ00	= α1β2 - α2β1 ;
	ms = 0	φ00	= α1β2 - α2β1 ;
	ms = 0
				φ	= α α
s = 1				11	1	2
				11	1	2
ms = 0, ±1			φ10 = α1β2 + α2β1
ms = 0, ±1				φ	= β β	2
				φ	= β β
				1-1	1

где s и ms – квантовые числа суммарного спина

, определяющие

S = S1

+ S2

с.з. операторов S

и Sz .

Решение:

Образуем вектор спина двухэлектронной системы:

S = S1

+ S2

(σ1

+ σ2 )

и построим операторы S

и S z :

2 2

S =

1 +σ 2 + 2 σ1 σ2 ;

S z =

1z +

σ 2 z

Для примера рассмотрим лишь один вариант решения задачи. Например, до-

кажем, что функция ϕ11

является с.ф.

операторов

соответствующая

S z ,

с.з. S 2 = h2 s (s +1) = 2h2 и

= hm = h.

1 +σ2

+ 2σ1 σ2

α α

3δ+3δ

σ1x σ2x +σ

1y σ2 y +σ1z σ

α α

1 2

6δ α α

+ 2

1x α σ2x

σ1y α σ2 y α

+σ1z

α σ2z

6δ α α

+2(β β

+iβ iβ

+α α

)

1 2

(6α α

+ 2α α

)= 2h2α α

= h2s (s +1)ϕ

где s =1.

S z

ϕ11 =

σ1z

+σ

2 z α1α2

α2 σ1z

α1 +α1 σ 2 z

α2

= hα1α2

= hm

ϕ11 ,

где m

+1.

Здесь мы воспользовались результатами задач (3.12) и (3.13). 171

Задачи к главе IV

4.1. Найти волновую функцию частицы, движущейся в поле U(x), в квазиклассическом приближении с точностью до членов квадратичных по h .

Решение:

Подставляя в стационарное уравнение Шредингера

−	h	d 2ψ (x) +U (x)ψ (x) = Eψ (x)				(1)
	2m
волновую функцию вида		dx2
			i
				S (x)	,	(2)
		ψ(x) = eh

для S(x) получаем дифференциальное уравнение:
	ihS'' −S'2 +2m(E −U ) = 0 ,					(3)

где введено обозначение для производной S ' = dSdx .

Представим S(x) в виде разложения по степеням h точностью до квадратичных членов:

S(x) ≈ S	0	(x) + hS (x) + h2 S	2	(x) .	(4)
	0	1	2

Тогда из уравнения (3) получаем:

[2m(T −U ) − S0'2 ] +h[iS0'' − 2S0' S1' ] +h2[iS1'' − S1'2 −2S0' S2' ] ≈ 0 .

Здесь мы отбросили члены со степенями по h выше двух. Приравнивая нулю множители перед h , получаем систему уравнений для Si (x) :

S0'2 = 2m(E −U )

S0''

(5)

2 S0'

S2'

iS'' −S'2

2S0'

Вводя импульс частицы

p =

2m(E −U ) , для соответствующих поправок

получаем:

S0' = ± p S0

S0''

= ±∫ pdx

(6)

S '

; dS

ln p = i ln p .

(7)

2 S0'

2 p

Учитывая, что S'' =

p''

p − p'2

, для S

получаем:

1 2

S '

(− 1

p'' p − p'2

+ 1

p'2

) =

3 p'2

−

p''

;

8 p3

2 p 2

4 p2

172

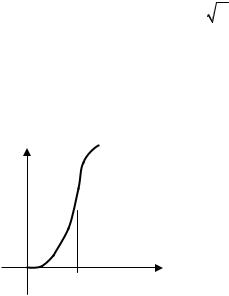
	3	∫	p'2		1	p''dx
S2 =	8			dx −	4
			p3			p2

Второй интеграл можно проинтегрировать по частям:

p''dx

p' + 2∫

p'2

∫

d ( dx ) =

Тогда

1 p'

p'2

∫

S2 = −

− 8

Производную p' можно выразить через силу F, действующую на части-

цу:

= dp

= mF ;

dt dx

(8)

F 2

1 mF

∫

S2 = −

8 m

dx −

4 p3 .

Таким образом, искомая волновая функция в рассматриваемом прибли-

жении имеет вид:

S ( x)

+hS

+h2S

)

S +iS

+ihS

2 ≈

ψ = eh

= eh 0

= eh

0 1

(9)

1− imh

− ihm

e±

≈ e

S0 +iS1 (1+ihS

) =

∫pdx

4 p

8 ∫

Появление мнимых поправочных членов в предэкспоненциальном множителе эквивалентно появлению такой же поправки в фазе волновой функции, причем эта поправка пропорциональна h.

∞ U (x)				4.2.		Получить правило квантования
					энергетических уровней и найти соответст-
		En			вующие	им квазиклассические волновые
					функции в случае потенциала, изображенного


					на рисунке 17. Получить квазиклассические
					уровни энергии частицы в однородном поле
					тяжести в случае, когда ее движение ограни-
	0		a	x	тяжести в случае, когда ее движение ограни-
	0		a	x	чено снизу идеально отражающей плоскостью.
					чено снизу идеально отражающей плоскостью.

Рис. 17.

Решение:

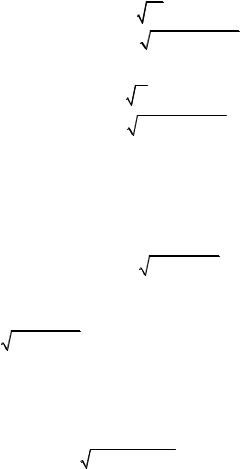
В квазиклассическом приближении волновые функции слева и справа от точки остановки (x = a) имеют вид:

173

exp(− 1

ψ ( x) =

∫

dx),

при x>a

h a

где

2m(U ( x) − E );

ψ (x) =

sin( 1

∫ pdx + π ), при 0 ≤ x<a

где p =

2m(E −U (x));

ψ (x) = 0,

при x ≤ 0.

Из последних двух условий находим искомое правило квантования:

π )

(0) = sin(

∫ pdx +

= 0

∫ 2m(E −U )dx +

= πn

так как левая часть всегда положительна, то n=1, 2, 3…

1 a

h ∫ 2m(E −U )dx = π(n +

1) − 4

= π(n + 4) , где n=0, 1, 2…

(1)

В однородном поле тяжести U(x)=mgx, уровни энергии находим из ус-

ловия (1):

, где a =

I = ∫ 2m(E − mgx)dx = πh(n +

)

Интеграл в левой части легко вычисляется подстановкой

t = 2m(E − mgx); dt = −2m2 gdx;

c пределами t = 2mE, t

= 0.

) ,

I =

(2mE)

= πh(n +

3m2 g

отсюда окончательно получаем:

9π2

E = (

mg2h2 )3

(n +

3)3

, n = 0,1, 2...

(2)

Обычно, квазиклассическое приближение применимо при n.1, но в

данном случае получено хорошее приближение и при n 1. В частности, при

n=0 из (4.2) получаем E				1	, причем точное значение для основного
n=0 из (4.2) получаем E			0	=1,84(mg 2h2 )3	, причем точное значение для основного
			0
уровня равно: E				1
уровня равно: E	0	=1,86(mg 2h2 )3 .
	0

174

U (x)


0	b (b-a) a	x

4.3.Для частицы, находящейся

вбесконечно глубокой потенциальной яме ширины a, найти в первом порядке теории возмущения смещение энергетических уровней под действием возмущения вида:

Рис. 18.	'	U	0	, b < x < a - b
	H =
		0, a - b < x < a; 0 < x < b.

Показать, что в этом приближении поправки первого порядка E(1)n для произвольного возмущения U(x) при достаточно больших n не зави-

сит от n.

Решение:

Как известно, волновые функции и уровни энергии частицы в бесконеч-

но глубокой яме равны:

ψ0 =

sin

πnx

, n =1, 2,3,...

π2h2

n2 .

Тогда

2ma2

a−b

(1)

ˆ '

2 πnx

= Hnn =

∫ψn

H ψn dx =

∫

dx sin

a−b

2πnx

a−b

∫ dx(1−cos

)

−

sin

) |b

2πn

(a −2b +

sin

2πnb

πn

α + β sin

α − β .

где учтено известное тождество: sinα −sin β =

2 cos

Так как H '

, а энергия частицы в яме E0

π 2h2

n2 , то условием примени-

ma2

мости теории возмущения ( Hmn' n En0 − Em0 ) является требование:

U0 nπ2h2 n2 , ma2

т.е. метод хорошо работает для достаточно узкой ямы и больших квантовых чисел n.

Для произвольного возмущения U(x):

	2	a	πnxdx =	1	a	2πnx
En(1) =		∫U (x) sin2			∫U (x)(1−cos		)dx.
	a			2
		0	a		0	a

175

Второе слагаемое, содержащее cos 2πanx , при n.1 быстро осциллирует, и сле-

довательно соответствующий интеграл стремится к нулю, так что поправка En(1) не зависит от n:

	1	a
En(1) ≈		∫U (x)dx.
	2
		0

4.4. На заряженный линейный гармонический осциллятор наложено однородное электрическое поле ε, направленное вдоль оси колебаний х. Рассматривая действие электрического поля как возмущение, рассчитать сдвиг энергетических уровней осциллятора.

Решение:

Из курса квантовой механики известно, что для осциллятора с полем

U (x) = mω2 x2

	где a =	h
	где a =	mω
		mω

решения УШ имеют вид:

En0 = hω(n + 12 ), n = 0,1, 2,...

	−	1 x	2		x	(1)

0		2 a	2
ψ n	= Ane			H n		,

				a

– нормировочная постоянная;	−	1		(x) – поли-
– нормировочная постоянная;	A = ( π 2n a n!)	2 , а H	n	(x) – поли-
	n		n

номы Чебышева-Эрмита, для которых, в частности, выполняются рекуррентные соотношения:

(x) =

n+1

(x) + nH

n−1

(x)

(2)

При включении однородного электрического поля оператор возмуще-

= −eεx . Эта задача также была решена в курсе квантовой меха-

ния равен H

ники (задача 3.2), где было показано, что

= hω(n + 1 ) −

e2ε2

(3)

2mω

По теории возмущения с точностью до квадратичных поправок энергия

системы равна:

H '

En = En0 + Hnn'

+ ∑

E0 −E0

где матричные элементы равны:

m≠n

+∞

' 0

+∞

Hmn =

∫ψm H

ψndx = −eε ∫ψm xψndx ≡ −eεxmn.

−∞

176

xmn = ∫ψm0 xψn0 dx = Am An ∫

Матричные элементы от координаты частицы не сложно вычислить, используя соотношение (2), значения нормировочных постоянных и свойство ортонормированности волновых функций осциллятора:

+∞

−∞

+∞

∫ψ0ψ0 dx =δmn .

n m .

−∞

+∞	dxe−	x2			x	xH		x	=
		a	H

−∞				m a			n a

+∞

−

+∞

−

aAm An ∫ dxe

+ naAm An ∫

Hn+1

dxe

Hn−1

−∞

+∞

∫

dxψ m xψ n+1 + na

∫

dxψm xψn−1

2(n +1)δm,n+1 +

δm,n−1

n+1 −∞

n−1 −∞

(4)

n +1

= a

δm,n+1 + a

δm,n−1.

При выводе формулы (4) в рекуррентном соотношении (2) произведена формальная замена x → ax . Отсюда для матричных элементов (4) получаем:


	0, m ≠ n ±1
		n +1
x		n +1	, m = n +1 .	(5)
x	= a		, m = n +1 .	(5)
mn		2
		n +1	, m = n −1
	a	n +1	, m = n −1
		2

Для разностей соответствующих уровней энергии имеем:

E0	− E0	= −hω,	при m = n +1;
n	m			(6)
E0	− E0	= hω,	при m = n −1.	(6)
E0	− E0	= hω,	при m = n −1.
n	m

Отсюда для энергий осциллятора в электрическом поле с точностью до квадратичных поправок окончательно получаем:

H '

En = En0

En(1) + En( 2)

= En0

+ Hnn'

+ ∑

− E

m≠n

2 (n +1)

2 n

(7)

= hω n

0 + e

−hω

hω

e2ε2 a2

e2ε2

= hω n

−

= hω n +

−

2hω

где учтено соотношение: a =

mω

177

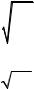
Полученный результат (7) совпадает с точным решением (3), следовательно, поправки третьего и более высоких порядков будут тождественно равны нулю. Это подтверждается и непосредственными расчетами.

4.5. Считая ядро равномерно заряженным шариком радиуса

R = 10-14 м, рассмотреть смещение основного уровня и расщепление возбужденного уровня энергии водородоподобного атома, обусловленные конечными размерами ядра.

Решение:

Для точечного ядра, когда потенциальная энергия взаимодействия электрона с ядром является кулоновской, невозмущенный гамильтониан имеет вид:

		h	2		Ze	2	.
H 0	= −			−
		2m			4πε	0r

Решение УШ в этом случае хорошо известно:

ˆ			0	0 0
H0ψnem = Enψnem ;
E	0	= −		me4		Z 2		;		(1)
E		= −		2h2 (4πε0 )2 n2				;		(1)
n				2h2 (4πε0 )2 n2
ψ	0		= R Y m (θ		,ϕ),
nlm				nl l
где Ze – заряд ядра; n=1,2,3…;				l=0,1,2…(n-1); m = 0, ±1,..., ±l;					Y m	– шаровая
									e
функция. Уровни энергии E0	являются k = n2						– кратно вырожденными, при-
n

чем вырождение по l является спецификой кулоновского потенциала, а по m –

центральной симметрией поля.

В частности,

основное

состояние

(n=1,

l=0, m=0) невырождено

( k = n2 =1):

m e4

1 Z 2e2

= −

2 = −

;

2h2

(4πε

0 )

2 a

ψ 0

≡

= R (r)Y 0

(θ,ϕ);

100

(2)

(r) = 2

Z 3

e−Z a ;

Y 0

(θ,ϕ) =

4π

h2 (4πε0 )

где a =

= 0,528

10−10 м – первый Боровский радиус. Первое возбужден-

m e2

ное состояние (n=2; l=0,1; m=0, ±1) четырехкратно вырождено k = n2 = 4 :

178

= −

m e4

= −

Z 2e2

;

2h2 (4πε0 )2 22

200

= R

(r)Y 0

(θ,ϕ) ≡ψ 0

;

Z r

Z 3 e− 2

(1− Z

);

(r) =

(3)

= R

(r)Y m (θ,ϕ) ≡ψ

0 , (m

21m

= 0, ±1);

Z 3

e−

Z r

(r) =

;

6a3

2 a

(θ,ϕ) =

cosθ

;Y ±1(θ,ϕ) =

sinθ e±iϕ ;

4π

8π

Таким образом, уровню энергии E2 соответствует четыре волновые

функции {ψ200 ,ψ210 ,ψ211,ψ21−1} ≡{ψ1,ψ2 ,ψ3 ,ψ4}.

Для построения оператора возмущения необходимо вычислить потенциальную энергию взаимодействия электрона с ядром в виде шара радиуса R и зарядом Ze . Этот результат хорошо известен из курса электродинамики:

−

(

− 1

r ≤ R;

R (4πε0 )

U (r) =

2 R

(4)

Ze2

−

r > R.

(4πε0 )r

Сравнивая последнее выражение с кулоновским потенциалом для то-

чечного ядра, когда U (r) = −

Ze2

для оператора возмущения получаем вы-

(4πε0 )r

ражение вида:

−

(

−

), r ≤ R;

=U (r) −U0 (r)

(4πε0 )r

(4πε0 )R

(5)

2 R

r > R.

а) Смещение основного уровня энергии атома.

Так как основной уровень не вырожден, то можно применять стационарную теорию возмущения для невырожденных состояний. В частности, поправка первого порядка малости равна диагональному матричному элементу:

E	'	'	* ˆ '				(6)
		= H00	= ∫ψ0 H ψ0 dV .	ˆ '	(5), а также
Используя волновую функцию (3), оператор						2	drdΩ
				H		dV = r

и условие нормировки ∫Y00 2 dΩ =1 , получаем:

179

	Z	3		R	−2Z	r		2		Ze	2	3		1	r	2
E' = 4				drr2e		a Ze			−		(		−				) .	(7)
	(4πε0 )a		3							R		2		2 R		2
				∫0			r

В нашем случае a 10−10 м, R 10−14 м, и даже при Z 100 показатель экспоненты 2ZRa < 2 10−2 является малым, и во всех дальнейших оценках будем

заменять exp(− 2aZr ) ≈1 . Тогда смещение основного уровня, вызванное конечностью размеров ядра, будет равно:

E' ≈ 4

Z 4e2

r4 ) =

2 Z 4e2

R 2

(8)

dr(r −

(4πε0 )a

5 a

∫0

Оценим относительное смещение основного уровня (2):

2 Z 4e2

R 2

1 Z 2e2

R 2

δ =

5 a

2 a

что даже для Z 100 является весьма малым δ 10−4 .

б) Расщепление первого возбужденного уровня энергии.

Так как поле “реального” ядра хотя и остается центральносимметричным, но уже не является кулоновским. Поэтому следует ожидать расщепление этого уровня на два подуровня, соответствующие различным l=0,1.

Так как уровень E20 является 4-х кратно вырожденным, то для нахождения первой поправки E' необходимо решить вековое уравнение вида:

(H ' − E' )	H '		H '	H '
11	(H '	12	13		14
H '	(H '	− E' )	H '	H	'		= 0 ,	(9)
21	22		23		24		= 0 ,	(9)
H31'	H32'		(H33' − E' )	H34'
'		'	'	'
'	H	'	'	'		'
H41	H	42	H43	(H44	− E )

где матричные элементы равны:


'	0* ˆ ' 0	* ˆ '		2	m* m '	.
Hmn =	∫ψm H ψndν = ∫Rm H			Rnr	dr ∫dΩYe Ye '	.
Так как шаровые функции ортонормированны как по верхнему, так и
по нижнему индексу, т.е.	Hmn' = ∫dΩYem*Yem'		' =δee'δmm' ,
	Hmn' = ∫dΩYem*Yem'		' =δee'δmm' ,

то все недиагональные элементы ( m ≠ n ) равны 0. Диагональные матричные элементы с учетом (3) в пренебрежении малыми членами, содержащими от-

ношение Ra 10−4 , будут равны:

180

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1718 / 2018 19 20 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.04.2015501.2 Кб569решебник.docx
#
18.04.201513.95 Кб13россия.docx
#
11.07.201913.89 Mб14Рубинштейн С.Л. Основы общей психологии.rtf
#
22.08.201930.64 Кб5русский СЕЛЕЗНЁВА(ТРХ-111).docx
#
25.09.201969.55 Кб7с группы.docx
#
22.03.20162.6 Mб61с.м.чернов_квантовая механика.pdf
#
18.04.2015197.73 Кб38савицкая .docx
#
18.04.2015173.57 Кб14Сведения о родителях 2014-2015.doc
#
18.04.2015447.02 Кб13Сельский туризм.pdf
#
15.08.201956.85 Кб1сем1.docx
#
11.11.2019243.71 Кб9Семаго содер и организ.doc