
с.м.чернов_квантовая механика
.pdf
В частности, H0 =1; H1 = 2ρ; H2 = 4ρ2 − 2; H3 =8ρ3 −12ρ, ... Легко проверить,
что полиномы Чебышева-Эрмита удовлетворяют рекуррентному соотноше-
нию:
Hn+1 = 2ρHn − 2nHn−1. |
(22.12) |
В целом, в.ф. осциллятора (22.9) удовлетворяет условию ортонормированно-
сти:
+∞ |
|
∫ψn (x)ψm (x)dx =δnm |
(22.13) |
−∞ |
Рассмотрим более подробно структуру энергетических уровней квантового осциллятора (22.8).
Во-первых, отметим, что расстояние между соседними уровнями энергии
одинаково для все уровней, независимо от n:
E = En+1 − En = hω.
Такие энергетические уровни называются эквидистантными.
Во-вторых, в отличие от классической и планковской теорий, наи-
меньшая энергия квантового осциллятора |
|
|
E = 1 hω ≠ 0 , |
(22.14) |
|
0 |
2 |
|
|
|
|
которая называется энергией нулевых колебаний.
Экспериментально энергия нулевых колебаний наблюдается в опытах по рассеянию света на монокристаллах, находящихся при абсолютном нуле температуры. На примере данной задачи, мы видим справедливость выполне-
ния важного принципа: в микромире запрещен абсолютный покой!
Покажем, что это свойство связано с корпускулярно-волновыми свойст-
вами материи, следствием которых являются соотношения неопределенности Гейзенберга.
Линейный осциллятор представляет собой частицу, которая совершает
гармонические колебания в области |
[−x0 ,+x0 ], имея |
|
неопределенность по |
|||||||||||
координате x = 2x . Тогда импульс частицы p |
|
|
p |
|
≥ |
h |
|
h |
. Следова- |
|||||
x |
x |
|
|
|||||||||||
0 |
|
|
|
|
|
|
|
|
x |
2x0 |
||||
тельно, энергия осциллятора имеет порядок: |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||
E = |
px2 |
+ mω2 x2 |
|
h2 |
+ mω2 x0 |
2 . |
|
|
|
(22.15) |
||||
2m |
8mx2 |
|
|
|
||||||||||
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
Минимальное значение функции (22.15) достигается при x02 = 2mhω , и
составляет Emin = E0 = 12 hω.
51
Замечание. Решение уравнения (22.7), удовлетворяющее стандартным условиям.
Рассмотрим решение уравнений вида:
d2ψ |
+ |
( |
λ −ρ2 ψ =0. |
(22.16) |
dρ2 |
|
) |
|
Найдем вначале асимптотику волновой функции при ρ →∞. В этом случае уравнение (22.16) примет вид:
d2ψ −ρ2ψ =0 dρ2
Непосредственной подстановкой легко проверить, что решением этого уравнения, убывающим на бесконечном удалении, является функция
−1 ρ2
ψ = e 2
.
Следовательно, решение исходного уравнения, имеющего правильную асимптотику, можно записать в виде:
|
− |
1 |
ρ |
2 |
|
|
2 |
H (ρ), |
(22.17) |
||
|
ψ = e |
|
|||
где H (ρ) – неизвестная функция. Подставляя выражение (22.17) в уравнение |
|||||
(22.16), получим соответствующее уравнение для этой функции: |
|
||||
d 2 H |
− 2ρ dH |
+(λ −1)H = 0. |
(22.18) |
||
d ρ2 |
d ρ |
|
|
|
|
Будем искать решение последнего уравнения в виде бесконечного ряда: |
|||||
H (ρ) = ak ρk + ak +1ρk +1 + ak +2 ρk +2 +... |
(22.19) |
||||
Чтобы не было расходимости волновой функции ψ при ρ →0 , необходимо потребовать, чтобы показатель низшей степени k ≥ 0. Подставляя разложение (22.19) в уравнение (22.18), получим уравнение вида:
k (k −1)ak ρk −2 + k (k +1)ak +1ρk −1 + (k + 2)(k +1)ak+2 −(2k +1−λ)ak ρk +... = 0 .
Так как последнее уравнение должно выполняться тождественно при любомρ ,то все коэффициенты следует приравнять нулю (с учетомk ≥ 0):
|
k =0; k =1; |
|
(22.20) |
||
a |
= a |
|
(2k +1− λ) |
. |
(22.21) |
k (k +1)(k + 2) |
|
||||
k +2 |
|
|
|
||
Так как ряд (22.19) может начинаться либо со степени k = 0, либо со степени k =1, то рекуррентная формула (22.21) определяет два ряда, содержащие либо четные, либо нечетные степени ρ :
Hчет = a0 + a2 ρ2 + a4ρ4 +...
52
Hнеч = a1ρ + a3ρ3 + a5ρ5 +...
Эти ряды являются независимыми частными решениями уравнения (22.18).
Исследуем поведение полученных рядов при ρ →∞. Рассмотрим, например, ряд с четными степенями ρ , и покажем, что при больших ρ он ведет себя асимптотически как exp(ρ2 ). Действительно:
exp(ρ2 )=1+ |
ρ2 |
|
ρ4 |
|
|
|
|
ρk |
|
ρk +2 |
|||||||||
|
+ |
|
|
+... + |
|
|
|
|
|
+ |
|
|
+... |
||||||
1! |
2! |
|
k |
|
|
k |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
! |
|
|
+1 ! |
||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
||||
При больших ρ наиболее существенными являются высшие члены k.1: |
|||||||||||||||||||
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
bk +2 |
|
|
|
! |
|
|
1 |
|
|
|
2 |
|
|
|
|
|
||
|
= |
|
|
2 |
|
= |
|
|
≈ |
|
. |
|
|
|
|||||
|
bk |
|
k |
|
|
k |
|
|
|
k |
|
|
|
||||||
|
|
|
|
|
+1 |
|
|
|
|
|
|||||||||
|
|
|
|
|
+1 ! |
|
2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
С другой стороны, из рекуррентной формулы (22.21) для k.1, имеем: |
|||||||||
|
ak +2 |
|
(2k +1−λ) |
2k 2 |
|
|
|||
|
|
= |
|
≈ k2 = |
|
. |
|
|
|
|
ak |
(k +1)(k + 2) |
k |
|
|
||||
Таким образом, для бесконечного ряда H (ρ)→ exp(ρ2 ) и при ρ →∞ полная |
|||||||||
|
|
|
|
|
|
|
ρ2 |
|
|
волновая функция (22.17) также расходится: ψ → exp |
|
→ ∞. Таким обра- |
|||||||
2 |
|||||||||
|
|
|
|
|
|
|
|
||
зом, требование ограниченности в.ф. приводит к необходимости оборвать ряд на конечном члене k = n , так что функция H (ρ)превращается в полином
n -ой степени Hn (ρ):
|
|
|
|
an ≠ 0; |
an+2 = 0. |
|
|
|
|
|
|
|
||||||
Отсюда получаем искомое требование: |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
λ = 2n +1. |
|
|
|
|
|
|
|
|
(22.22) |
|||
Найдем, наконец, волновые функции осциллятора. Для этого положим в |
||||||||||||||||||
рекуррентной формуле (22.21) k = n − 2 и λ = 2n +1, тогда: |
|
|
|
|
||||||||||||||
a |
|
= a |
|
(2(n − 2)+1−(2n +1)) |
= − |
|
22 |
a |
|
или |
||||||||
|
|
|
(n −1)n |
|
|
n |
(n −1) |
|
||||||||||
|
n |
|
n−2 |
|
|
|
n−2 |
|
|
|||||||||
|
|
|
|
a |
|
= − |
n(n −1) |
a . |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
n |
−2 |
|
|
22 |
n |
|
|
|
|
|
|
|
||
Аналогичным способом, легко получить выражение: |
|
|
|
|
|
|||||||||||||
a |
= −(n − 2)(n −3)a |
= |
n(n −1)(n − 2(n −3)) |
a |
|
. |
||||||||||||
|
|
|||||||||||||||||
n−4 |
|
|
23 |
|
n−2 |
|
|
|
|
25 |
|
|
|
n |
|
|||
Таким образом, искомая функция должна иметь вид полинома:
H |
|
(ρ)= a |
|
ρn − |
n(n −1) |
ρn−2 |
+ |
n(n −1)(n − 2)(n −3) |
ρn−4 |
−... |
. (22.23) |
|
n |
n |
|
|
|||||||||
|
|
2 |
2 |
|
5 |
|
|
|
||||
|
|
|
|
|
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
53 |
|
|
|
|

В силу линейности уравнения (22.18), множитель an может быть взят произвольным, но для согласования с математическими построениями Чебышева – Эрмита будем использовать an = 2n.
§ 23. Линейный гармонический осциллятор. Операторная форма
Решим предыдущую задачу, используя абстрактный формализм операторов квантовой механики. Причем, ограничимся поиском лишь уровней энергии осциллятора.
Для одномерного осциллятора гамильтониан имеет вид:
H^ = |
p^2x |
+ |
mω2 x$2 |
, |
(23.1) |
2m |
|
||||
|
2 |
|
|
||
где операторы x$ и p^ x удовлетворяют коммутационному условию:
$ |
^ |
|
= ih. |
(23.2) |
x, p x |
||||
Покажем, что только на основании этих коммутационных условий можно определить энергетические уровни осциллятора. Прежде всего, перейдем от
размерных параметров x$ и p^ x к безразмерным характеристикам X^ и P^x
согласно условию:
$ |
2h |
|
|
|
|
2mhωP^ |
|
|
|
x ≡ |
|
X^; |
p^ |
x |
≡ |
|
x. |
(23.3) |
|
mω |
|
||||||||
Тогда исходные соотношения (23.1) и (23.2) примут вид: |
|
||||||||
|
H^ = hω(P^ |
2x |
+X^ |
2 ); |
|
(23.4) |
|||
|
^ |
^ |
|
|
i |
|
|
|
|
|
= |
|
. |
|
(23.5) |
||||
|
X |
, P x |
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
Далее, введем новые операторы, физический смысл которых выясним ниже: a^ ≡ X^ +iP^x; a^ + = X^ + − iP^+ = X^−i P^x. (23.6)
Здесь мы воспользовались свойством эрмитовости операторов координаты и импульса. Обратный переход имеет вид:
X^ = 12 (a^ +a^+ |
); |
P^ |
x = |
1 |
(a^ −a^+ ). |
(23.7) |
||
2i |
||||||||
Тогда условие (23.5) примет вид: |
|
|
|
|
|
|
|
|
|
$ $ |
+ |
=1. |
|
|
|
(23.8) |
|
a,a |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
$ |
|
$ |
+ |
, с учетом соотношения (23.8): |
||
Выразим также оператор H^ (23.4) через a |
|
и a |
|
|||||
|
54 |
|
|
|
|
|
|
|
|
+ |
+ |
1 |
|
H^ = hω a^ a^ |
|
2 |
. |
|
|
|
|
|
Отсюда, в частности, легко получить следующие полезные соотношения:
H^ |
,a^+ = hωa^+; |
(23.9) |
|
|
|
|
|
[ H^ ,a ^]= −hω a.^ |
(23.10) |
||
Пусть ψ – с.ф. оператора H^ , соответствующая с.з. энергии E , т.е. |
|||
|
|
H^ψ = Eψ. |
(23.11) |
$ |
$ |
+ |
|
Покажем, что в.ф. ( aψ ) и ( a |
ψ ) также являются с.ф. оператора H^ , но |
||
соответствующие энергиям E′ = E − hω и E′′= E +hω, |
т.е. |
||
H^ (a^ |
ψ ) = (E − hω)(a^ψ ); |
(23.12) |
|
H^(a^+ψ )= (E + hω)(a^+ψ ). |
(23.13) |
||
Докажем, например, первое равенство с учетом (23.9):
^ |
|
H |
^ |
a^ )ψ = |
( a ^H |
^ |
|
|
^ |
|
= |
|||
H (a^ψ )= ( |
|
−hω a ^)ψ = a H^ ψ −hωaψ^ |
||||||||||||
= E aψ^ |
−hω aψ^ |
= (E −hω) aψ^ . |
|
|
|
|
|
|||||||
Из уравнений (23.12) и (23.13) следует, что: |
|
|
|
|
|
|||||||||
|
|
H^ |
(a ^n ψ |
) |
= (E − nhω)a ^nψ; |
|
) |
|
|
(23.14) |
||||
|
|
|
|
(( |
|
) |
n |
) |
( |
|
n |
|
||
|
|
H |
^ |
a ^ |
+ |
ψ = (E + nhω) a ^ |
+ |
|
ψ. |
|
||||
|
|
|
|
|
|
|
|
|
||||||
Отсюда видно, что осциллятор имеет дискретные, равноудаленные на hω уровни энергии.
Найдем, наконец, минимальную энергию осциллятора. Пусть ψ0 – с.ф.
осциллятора, соответствующая наименьшему значению энергии E0 . Это означает, что a$ψ0 = 0, тогда:
H^ψ |
|
= hω |
a ^+ a ^ + |
1 ψ |
= |
hω |
ψ |
. |
||
0 |
|
|||||||||
|
|
|
2 |
|
0 |
2 |
0 |
|
||
|
|
|
|
|
|
|
|
|||
Отсюда получаем E = |
hω |
|
, и следовательно, в целом, энергия осциллятора |
||||||
|
|||||||||
0 |
2 |
|
|
|
|
|
|
|
|
равна: |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
En |
|
|
где n = 0,1,2,... |
(23.15) |
||||
|
= hω n + |
2 |
, |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
$ |
$ |
+ |
. Как |
Теперь можно определить физический смысл операторов a и a |
|
||||||||
|
$ |
|
|
|
|
перево- |
|||
было показано, оператор a при действии на состояние с энергией E |
|||||||||
дит его в состояние с энергией (E − hω), т.е. “отбирает” квант энергии hω . Поэтому оператор a$ имеет смысл оператора уничтожения. Напротив, опе-
55
ратор a$+ переводит квантовую систему в состояние с энергией (E + hω) и на-
зывается оператором рождения. Учитывая, что энергия осциллятора (23.15) линейно зависит от целого числа n , то этому выражению можно придать иную физическую интерпретацию. В частности, можно утверждать, что наша система состоит из n одинаковых квазичастиц с энергией hω каждый, называемые фононами (по аналогии с квантами электромагнитного поля – фотонами). Эта идея нашла широкое распространение в физике (экситоны, поля-
роны, плазмоны и т.д.), и является отражением корпускулярно-волновых свойств материи.
Введенные операторы играют фундаментальную роль в квантовой теории поля, описывающей процессы излучения и поглощения энергии, и позволяют в общем виде определять свойства любых квантовых систем с переменным числом частиц.
§ 24. Прохождение частиц через потенциальный барьер
Пусть частица массой m движется вдоль оси 0x с энергией E и на своем встречает потенциальный барьер U(x), максимальная высота которого
(Рис. 6).
U (x)
U0
E
0 |
x1 |
x2 |
x |
|
|
Рис. 6 |
|
|
|
Классическая частица |
не может |
попасть в |
область x1 ≤ x ≤ x2 , где |
|
U (x)> E , в |
противном |
случае |
кинетическая |
энергия частицы: |
Px2 = E −U (x)< 0 , что физически недопустимо. Следовательно, она может
2m
двигаться лишь в области x ≤ x1 .
Однако квантовая частица может проходить через барьер без измене-
ния полной энергии. Это явление называют туннельным эффектом. Количе-
ственно туннельный эффект будем описывать параметром:
D = |
j3 |
, |
( 0 ≤ D ≤ 1 ) |
(24.1) |
|
j |
|||||
|
|
|
|
||
|
0 |
|
|
|
|
|
|
|
56 |
|

где |
j 3 – плотность потока частиц, прошедших за барьер; |
j 0 |
– плотность потока частиц, падающих на барьер. |
Параметр D называется коэффициентом проницаемости (прозрачности) барьера.
Для простоты рассмотрим вначале прохождение частицы через прямоугольный потенциальный барьер высотой U0 и шириной a (рис. 7):
U (x) |
II |
|
|
|
0 , |
|
x < 0 , x > a ; |
I |
III |
|
U |
(x ) = |
|
||
|
|
, |
0 ≤ x ≤ a . |
||||
|
|
|
|
|
U 0 |
||
E |
|
x |
|
|
|
|
(24.2) |
|
Будем считать, что E |
|
< U 0 . |
||||
0 |
a |
|
|
||||
|
|
|
|
|
|
||
|
Рис. 7 |
Для расчета D необходимо провести следую- |
||
|
|
щие вычисления: |
|
|
1. |
Для заданного U(x) написать одномерное уравнение Шредингера, и |
|||
найти решение Ψ(x) в трех областях Ψ1(x), Ψ2 (x), Ψ3(x). |
|
|||
2. |
Необходимо обеспечить выполнение стандартных условий (условий |
|||
сшивания решений на границе областей): |
|
|||
|
Ψ1(0)= Ψ2 |
(0), |
Ψ1′ (0 ) = Ψ ′2 (0 ), |
(24.3) |
|
ψ2 (a)=ψ3 (a), |
ψ2′(a)=ψ3′(a). |
|
|
3. Зная волновые функции, найти плотность тока вероятности для падающих и прошедших барьер частиц:
|
h |
|
|
* |
∂Ψ |
|
∂Ψ |
* |
jx = |
|
|
Ψ |
|
− Ψ |
|
|
|
|
|
|
|
|||||
|
|
|
∂x |
∂x |
. |
|||
|
2mi |
|
|
|
|
|||
Предположим, волновая функция имеет вид Ψ = Α e плотность тока вероятности равна:
jx = |
h |
(Α*e−ikx Αeikxik − Αeikx (−ik )Α*e−ikx )= |
hk |
|
Α |
|
2 . |
|
|
|
|||||||
2mi |
m |
|||||||
|
|
|
|
|
|
4. Зная потоки, найти коэффициент проницаемости D.
Запишем одномерное стационарное уравнение Шредингера:
(24.4)
ik x , тогда
(24.5)
|
d 2 Ψ |
+ |
2 m |
(E − U (x ))Ψ = 0 . |
|||||
|
|
|
|
||||||
|
dx 2 |
h 2 |
|
|
|||||
Это уравнение во всех трех областях принимает вид: |
|||||||||
|
|
d 2 Ψi |
+ ki |
2 Ψi = 0 , |
где i = 1, 2, 3, |
||||
|
|
|
|||||||
|
|
dx2 |
|
|
|
|
|
||
|
|
|
|
|
k1 = k3 = |
2mE |
, |
||
|
|
|
|
|
2 |
||||
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
57 |
|
|
|
(24.6)
(24.7)

k2 |
= |
|
2m |
(E −U 0 )= iχ , |
(24.8) |
||
|
2 |
||||||
|
|
|
h |
|
|||
|
χ = |
|
2m |
(U0 − E). |
(24.8) |
||
|
|
2 |
|||||
|
|
|
|
h |
|
||
Решения уравнения Шредингера (24.6) имеют вид: |
|
||||||
Ψi |
(x ) = Αieiki x + Βi e−iki x , |
(24.9) |
|||||
где e ik x описывает плоскую волну, распространяющуюся в положительном
направлении 0x, а e − ik x описывает отраженные волны. Очевидно, в третьей области (после барьера) должны отсутствовать отраженные волны, следовательно: Β 3 = 0 . Таким образом, решения уравнения во всех трех областях
имеют вид:
ψ 1 (x ) = Α 1e ik1 x + Β1 e − ik1 x ;
ψ 2 (x ) = Α 2 e − χ x + Β 2 e χ x ;
ψ 3 (x ) = Α 3 e ik1 x . |
|
|
|
(24.10) |
||||
Для нахождения оставшихся коэффициентов Ai и Bi |
обратимся к гра- |
|||||||
ничным условиям (24.3): |
|
|
|
|
|
|||
|
Α 1 + Β 1 = Α 2 + Β 2 ; |
|
|
|
|
|||
i k (Α 1 − Β 1 ) = χ (Β 2 − Β 1 ); |
|
|
|
|||||
|
Α 2 e − χ a + Β 2 e χ a = Α 3 e i k 1 a ; |
|
|
|
||||
|
χ (Β 2 e χ a |
− Α 2 e − χ a ) = i k 1 Α 3 e i k 1 a . |
|
|
(24.11) |
|||
Решая полученную систему алгебраических уравнений, можно найти |
||||||||
все коэффициенты и, в частности, отношения амплитуд: |
|
|
|
|||||
|
Α 3 |
2 i k 1 χ e |
− i k 1 a |
|
. |
(24.12) |
||
|
|
|
||||||
|
Α 1 |
= |
(k 12 |
− χ 2 )s h χ a + 2 i k 1 χ c h χ a |
|
|||
Разделив поток частиц в третей области |
j = |
hk1 |
|
|
Α |
|
2 |
j |
|
= |
hk1 |
|
|
Α |
|
||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
3 |
на |
0 |
|
1 |
||||||||||||||||||||||
3 |
m |
|
|
|
|
m |
|
|
|
||||||||||||||||||||
ходим: |
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
D = |
j3 |
|
|
|
Α 3 |
|
|
Α 3 |
|
|
|
4 k12 χ 2 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
= |
|
|
|
|
|
|
|
= |
|
|
= |
|
|
|
|
|
|
|
|
|
||||||||
j0 |
|
|
Α1 |
|
|
|
2 |
Α1 |
(k12 − χ 2 )2 sh 2 χa + 4 k1 |
2 χ 2 ch 2 χa |
. |
|
|||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Учитывая соотношение ch2 χa − sh2 χa = 1 , тогда окончательно чим формулу для коэффициента проницаемости D:
2
, на-
полу-
D = |
4 k 12 χ 2 |
2 χ 2 . |
(24.13) |
(k 12 + χ 2 )2 sh 2 χa + 4 k 1 |
В атомной физике, как правило, выполняется условие χa >> 1 , так что
58
sh2 χa ≈ 14 e2 χa .
Тогда в этом приближении D можно записать в виде:
|
2m (U0 |
|
|
D ≈ e−2χa = exp −2a |
− E) . |
(24.14) |
|
|
h2 |
|
|
Замечание 1.
Туннельный эффект играет основную роль лишь в областях микроскопических явлений. Рассмотрим, например, масштабы ядерной физики:
a =10−15 м, |
m = mp =1,64 10−27 кг |
|
||
U0 − E 10МэВ =1, 6 10−12 Дж , |
2 a |
2 m (U 0 − E ) ≈ 1 , |
||
h |
||||
|
|
|
||
следовательно D ≈ e−1 ≈ 0,3.
Таким образом, 30% ядерных частиц постоянно участвуют в туннельном эффекте (α-распад ядер).
Замечание 2. |
|
|
|
|
|
|
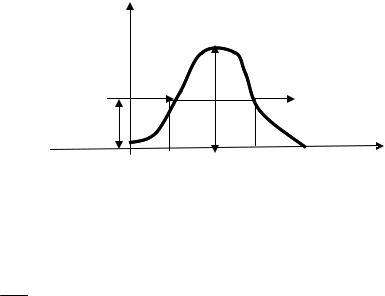
Получим D для барьера произвольной формы. Для этого интерполируем |
||||||
гладкую кривую U (x) |
прямоугольными ступеньками ширины xi и высотой |
|||||
U (xi ), для каждой из которых коэффициент проницаемости равен: |
||||||
|
D = exp − |
2 |
x |
2m(U (x )− E) |
||
|
|
|||||
|
i |
|
h |
i |
i |
|
|
|
|
|
|
|
|
Тогда полный коэффициент проницаемости для всех ступенек:
x |
→0 |
i |
|
2 |
∑ i |
( |
i |
|
|
2x2 |
( |
i |
) |
|
|||
|
|
|
) |
|
|
|
∫ |
|
|||||||||
D= lim |
ΠD |
=exp − |
|
|
x |
2m U(x )−E |
|
=exp − |
|
|
|
2m U(x )−E dx , (24.15) |
|||||
|
|
|
|
h |
i |
|
|
|
h |
x |
|
|
|
|
|||
i |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где интегрирование проводится по запрещенной области x1 ≤ x ≤ x2 , где потенциальная энергия U (x)≥ E .
Замечание 3.
Рассмотрим вопрос о знаке кинетической энергии под барьером. Для этого рассмотрим барьер бесконечной ширины, в котором волновая функция имеет вид:
Ψ 2 |
= A2 e − χ x , где χ = |
1 |
2m(U0 |
− E) |
. |
|
|
h |
|
|
Из вида волновой функции видно, что вероятность нахождения частиц под барьером экспоненциально уменьшается, то есть можно считать, что час-
тица заходит на расстояния не далее x ~ χ1 . Тогда из соотношения неопре59
деленности Гейзенберга: px ~ px > hx =hχ= 2m(U(x)−E), и неопределенность кинетической энергии превышает величину
|
|
|
P2 |
|
h2 |
χ |
|
|
|
− E . |
|
|
|
|
|
|
|
|
ΔΤ = |
x |
> |
|
|
|
= U 0 |
|
|
|
|
|
|
||||
2m |
2m |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таким образом, эта энергия вместе со своей неопределенностью будет |
|||||||||||||||||
неотрицательна, т.е. под барьером: |
(T + |
|
Τ) ≥ 0. |
|
|
|
|
|
|
||||||||
Замечание 4. Надбарьерное отражение. |
|
|
|
|
|
|
|||||||||||
Пусть E >U0 , тогда k2 становится действительным числом. |
При этом |
||||||||||||||||
соотношение для D сохраняет свой вид (24.13), если произвести формальную |
|||||||||||||||||
замену χ на (−ik2 ). При этом учтем условие: |
sh2 (−ik2a)= −sin2 k2a. |
|
|
|
|||||||||||||
Тогда для коэффициента проницаемости D получаем: |
|
|
|
|
|
||||||||||||
D = |
−4 k12 k 2 |
2 |
|
|
|
|
|
|
= |
|
|
1 |
|
|
|
|
|
− (k12 − k 2 2 )2 sin 2 k 2 a − 4 k1 |
2 k 2 2 |
1 + |
(k12 − k 22 |
)2 |
k |
|
a |
||||||||||
|
|
|
|
|
|
|
|
|
|
4 k12 k 22 |
sin 2 |
1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
.
Отсюда следует, что частица беспрепятственно пролетает над ямой,
как и классическая частица, когда D=1. При этом возможны два случая:
1. k1 = k2 , (U0 = 0); физически это соответствует отсутствию потенциальной ступеньки.
2. sin k2a = 0 , k2a = πn , E =U0 |
+ |
h2k2 |
|
|||
|
2 |
. |
||||
|
|
|
||||
|
|
2m |
|
|||
|
π 2h2 |
|
||||
Это возможно, когда E = U0 + |
|
|
|
n2 |
, n=1, 2, 3,…, которое совпадает |
|
2ma |
2 |
|||||
|
|
|
|
|
||
с уровнями энергии в бесконечно глубокой потенциальной яме, то есть частица беспрепятственно проходит над барьером при определенных дискретных значениях энергии. В противном случае, D<1 и частица испытывает надбарьерное отражение. Этот эффект отсутствует в классической физике.
§ 25. Одномерная модель кристалла Кронига-Пенни
Известно, что кристаллические твердые тела состоят из периодически расположенных в пространстве положительно заряженных ионов, в поле которых движутся свободные электроны. Можно представить себе одномерную модель кристалла, когда электроны движутся в периодическом поле в виде прямоугольных барьеров.
Пусть имеется бесконечно протяженное периодическое поле вида:
60
