
- •Предисловие
- •5. Работа внутренних сил плоской стержневой системы
- •6. Принцип возможных перемещений и упругие системы
- •9. Теорема о взаимности перемещений
- •10. Теорема о взаимности реакций
- •11. Теорема о взаимности реакций и перемещений
- •14. Теорема Лагранжа
- •18.1. Понятие о матрице перемещений
- •18.2. Вычисление интегралов формулы Мора в матричной форме в случае произвольных подынтегральных функций
- •18.4. Определение перемещений от силового воздействия
- •18.5. Определение перемещений от температурных воздействий
- •18.6. Определение перемещений от кинематических воздействий
- •1.7. Определение перемещений от совместных воздействий различного характера
- •5.1. РАСЧЕТ ОДНОПРОЛЕТНОЙ БАЛКИ
- •5.2. РАСЧЕТ ЛОМАНОГО БРУСА
- •5.3. РАСЧЕТ ТРЕХШАРНИРНОЙ РАМЫ
- •5.4. РАСЧЕТ ФЕРМЫ С ТРЕУГОЛЬНОЙ РЕШЕТКОЙ (АНАЛИТИЧЕСКИЙ СПОСОБ)
- •5.5. РАСЧЕТ ФЕРМЫ С ТРЕУГОЛЬНОЙ РЕШЕТКОЙ (ГРАФИЧЕСКИЙ СПОСОБ)
- •6.1. КИНЕМАТИЧЕСКИЙ АНАЛИЗ ЗАДАННОЙ РАСЧЕТНОЙ СХЕМЫ
- •6.2. ЗАМЕНЯЮЩАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ ЭЛЕМЕНТАРНЫХ РАСЧЕТНЫХ СХЕМ
- •6.3. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ
- •6.7. ПРОВЕРКА ПОЛУЧЕННОГО РЕШЕНИЯ ЗАДАЧИ
- •7.2. ПОСТРОЕНИЕ НАПРАВЛЯЮЩИХ ЭПЮР
- •7.3. РЕАЛИЗАЦИЯ МАТРИЧНОЙ ФОРМЫ ВЫЧИСЛЕНИЯ ПЕРЕМЕЩЕНИЙ
- •7.3.1. РАЗРАБОТКА СХЕМЫ ДИСКРЕТИЗАЦИИ
- •7.3.2. МАТРИЧНАЯ ФОРМА ПРЕДСТАВЛЕНИЯ ГРУЗОВОЙ И НАПРАВЛЯЮЩЕЙ ЭПЮР
- •7.3.3. ПОСТРОЕНИЕ МАТРИЦЫ ПОДАТЛИВОСТИ
- •7.3.4. ПРИЕМЫ МИНИМИЗАЦИИ РАЗМЕРОВ МАТРИЦЫ ПОДАТЛИВОСТИ
- •7.4. ПРОВЕРКА ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ
- •8.1. КИНЕМАТИЧЕСКИЙ АНАЛИЗ ЗАДАННОЙ РАСЧЕТНОЙ СХЕМЫ
- •8.2. КЛАССИФИКАЦИЯ СТЕРЖНЕЙ РЕШЕТКИ ФЕРМЫ
- •8.3. ОПРЕДЕЛЕНИЕ УСИЛИЙ В СТЕРЖНЯХ ГРАФИЧЕСКИМ СПОСОБОМ
- •8.5. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ НА ОСНОВЕ ЛИНИЙ ВЛИЯНИЯ
- •9.1. ПОСТАНОВКА ЗАДАЧИ РАСЧЕТА
- •9.3. ВЫБОР ОСНОВНОЙ СИСТЕМЫ МЕТОДА СИЛ
- •9.4. КАНОНИЧЕСКАЯ СИСТЕМА УРАВНЕНИЙ МЕТОДА СИЛ
- •9.5. МАТРИЧНАЯ ФОРМА МЕТОДА СИЛ
- •9.5.1. РАЗРАБОТКА СХЕМЫ ДИСКРЕТИЗАЦИИ
- •9.5.4. ФОРМИРОВАНИЕ КАНОНИЧЕСКОЙ СИСТЕМЫ УРАВНЕНИЙ
- •9.5.5. РЕШЕНИЕ КАНОНИЧЕСКОЙ СИСТЕМЫ УРАВНЕНИЙ
- •9.7. КОНТРОЛЬ ПРАВИЛЬНОСТИ РЕШЕНИЯ ЗАДАЧИ
- •10.1. ПОСТАНОВКА ЗАДАЧИ РАСЧЕТА
- •10.2. НАЗНАЧЕНИЕ СИСТЕМЫ ДОПОЛНИТЕЛЬНЫХ СВЯЗЕЙ ДЛЯ СОЗДАНИЯ ЗАМЕНЯЮЩЕЙ СИСТЕМЫ ОДНОПРОЛЕТНЫХ БАЛОК
- •10.3. ОСНОВНАЯ СИСТЕМА МЕТОДА ПЕРЕМЕЩЕНИЙ
- •10.4. КАНОНИЧЕСКАЯ СИСТЕМА УРАВНЕНИЙ МЕТОДА ПЕРЕМЕЩЕНИЙ
- •10.5 СТАНДАРТНЫЕ ЭПЮРЫ МЕТОДА ПЕРЕМЕЩЕНИЙ
- •10.6. ГРУЗОВАЯ И ЕДИНИЧНЫЕ ЭПЮРЫ МЕТОДА ПЕРЕМЕЩЕНИЙ
- •10.7. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ И СВОБОДНЫХ ЧЛЕНОВ КАНОНИЧЕСКОЙ СИСТЕМЫ УРАВНЕНИЙ МЕТОДА ПЕРЕМЕЩЕНИЙ
- •10.9. ОПРЕДЕЛЕНИЕ ОРДИНАТ ЭПЮРЫ ИЗГИБАЮЩЕГО МОМЕНТА В ЗАДАННОЙ РАСЧЕТНОЙ СХЕМЕ

18.1. Понятие о матрице перемещений
В инженерных расчѐтах часто возникает необходимость определения группы различных перемещений узлов и сечений заданного сооружения от независимых друг от друга внешних воздействий – силовых, температурных, кинематических. Таблица величин этих перемещений, составленная по определенным правилам, называется матрицей перемещений.
Например, в раме, показанной на рис. 18.1, требуется определить горизонтальное перемещение узла А, вертикальное перемещение сечения "к" и угол поворота сечения "а" отдельно от равномерно распределенной нагрузки q, сосредоточенной силы F, сосредоточенного момента М, изменения температуры tο1, tο2, tο3 и смещения опорных связей (1), (2). Установим следующий порядок формирования матрицы
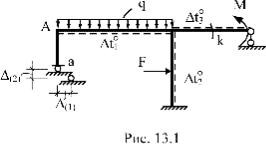
перемещений. В её
первой строке будем фиксировать только величины горизон- тального перемеще- ния узла А, во второй
–вертикального пере- мещения сечения "к", в третьей – угла пово-
рота сечения "а". Порядок записи величин искомых переме-
щений в каждой строке зависит от принятой нумерации внешних воздействий. Для нашего примера примем: первое воздействие – равномерно распределённая нагрузка q, второе
–сосредоточенная сила F, третье – сосредоточенный момент
М, четвёртое – изменение температуры Dt1o , Dto2 , Dto3 , пятое –
смещение опорных связей D(1), D(2). С учётом установленных
правил получим матрицу перемещений
|
æD(q) |
D(F) |
D(M) |
D(t) |
D(c) ö |
|
|
ç |
Ax |
Ax |
Ax |
Ax |
Ax |
|
ç |
(q) |
(F) |
(M) |
(t) |
(c) |
D = |
çDky |
Dky |
Dky |
Dky |
Dky . |
|
|
çq(q) |
q(F) |
q(M) |
q(t) |
q(c) |
|
|
è |
a |
a |
a |
a |
a ø |
Вобщем случае для любой задачи число строк матрицы перемещений равно числу определяемых перемещений раз- личного характера, а число столбцов – числу независимых внешних воздействий (собственный вес конструкций, снег, ветер, технологическая нагрузка, изменение температуры, смещение опорных связей и т.д.). В первом столбце матрицы перемещений принято записывать группу искомых переме- щений от постоянной нагрузки.
Внастоящей лекции рассматривается вычисление эле- ментов матриц перемещений в матричной форме. Для ус-
пешного усвоения материала этой и последующих лекций
читателям полезно повторить некоторые разделы линейной алгебры, связанные с действиями транспонирования, сложе- ния, вычитания, умножения и обращения матриц.
18.2. Вычисление интегралов формулы Мора в матричной форме в случае произвольных подынтегральных функций
Определённые интегралы всех членов формулы Мора |
|
||||||
nM lk Mik (s)MFk (s)ds |
nQ lk |
Qik (s)QFk (s)ds |
+ |
||||
D jk = å ò |
EJk (s) |
+ å ò kτk |
|
GAk (s) |
|||
k=1 0 |
k=1 0 |
|
|
||||
|
nN lk Nik (s)NFk (s)ds |
|
|||||
|
+ å |
ò |
|
|
|
|
|
|
|
EAk (s) |
|
|
|
||
|
k=1 |
0 |
|
|
|
|
|
имеют одинаковую структуру и в обобщённой форме могут быть представлены следующим образом:
lk F |
ik |
(s)F |
Fk |
(s)ds |
. |
(18.1) |
|
ò |
|
|
|
||||
|
|
Tk (s) |
|
||||
0 |
|
|
|
|
|
||
Здесь Фik(s) – общее представление функций внутренних усилий Мik(s), Qik(s), Nik(s) от единичного фактора, прило-
женного в направлении определяемого перемещения; ФFk(s) – представление функций внутренних усилий МFk(s), QFk(s), NFk(s) от заданного силового воздействия; Tk(s) – представле- ние функций, описывающих изменение жесткостей попереч- ных сечений EJk(s), GAk(s), EAk(s) и параметра kτk вдоль оси k-го грузового участка.
Численное значение определённого интеграла (18.1)
можно получить по формуле Симпсона в матричной форме
lk Fik (s)FFk (s)ds |
|
|
æ |
(в) |
|
(в) |
|
(с) |
(с) |
|
(е) |
|
(е) ö |
|
|||||
= |
lk ç Fik |
|
F Fk |
+ 4 |
Fik |
|
F Fk |
+ |
Fik |
|
F Fk |
= |
|||||||
ò |
|
|
ç |
|
|
|
|
|
|
|
|
|
|||||||
T (s) |
6 |
T |
(в) |
|
T |
(с) |
T |
(е) |
|
||||||||||
0 |
|
ç |
k |
|
|
k |
|
k |
|
|
|
||||||||
|
k |
|
|
è |
|
|
|
|
|
|
ø |
|
|||||||
|
|
|
|
|
FТ |
P |
F= . |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
ik |
k |
Fk |
|
|
|
|
|
|
|
|
|
|||
В соотношении (18.2):
éêF(ikв) ùú Fik = êêF(ikс) úú ; êF(е) ú ë ik û
|
|
|
é |
1 |
|
|
|
ê |
|
|
|
|
|
|
|
l |
|
êT(в) |
|
|
k |
ê |
k |
|
P = |
|
ê |
0 |
|
|
|
|||
k |
6 |
ê |
|
|
|
|
|
ê |
0 |
|
|
|
ê |
|
|
|
|
ê |
|
|
|
|
ë |
|
Т
ik
0
4
Tk(c)
0
[F(в) F(с) F(е) ]=;FF |
Fk |
= |
|||||||||
|
ik |
ik |
|
ik |
|
|
|
|
|||
|
|
|
|
|
|
|
|||||
|
|
ù |
|
|
é |
T0 |
0 |
|
|
||
0 |
|
ú |
|
|
ê |
|
|
||||
|
|
|
|
|
|
||||||
|
|
ú |
l |
|
êT(в) |
|
|
|
|
|
|
|
|
ú |
k |
ê |
k |
|
T |
|
|
||
|
|
|
|
ê |
|
|
|
0 |
|
|
|
0 |
|
ú = |
6T |
0 |
4 T(c) |
|
|
||||
|
ê |
|
|
||||||||
1 |
|
ú |
|
0 |
ê |
|
|
|
k |
|
|
|
ú |
|
|
|
|
|
|
|
|
||
|
|
ú |
|
|
ê |
0 |
0 |
|
|
||
T(e) |
|
|
|
|
|||||||
ú |
|
|
ê |
|
|
|
|
|
|
||
k |
|
|
|
ë |
|
|
|
|
|
|
|
|
û |
|
|
|
|
|
|
|
|
||
FikT – матрица, транспо- нированная по отноше- нию к матрице Фik;
Fik(в) , F(Fkв) , Tk(в) – значе-
ние функций, входящих в
подынтегральное выра- жение (1 .1) в начале ин-
éêF(Fkв) ùú êêF(Fkс) úú ; êF(е) ú ë Fk û
ù
0 ú
ú
ú
0 ú ;
ú
T0 úú
T(e) ú
k û
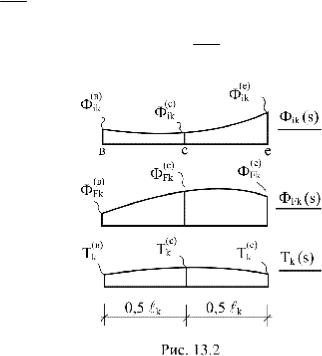
тервала; Fik(c) , F(Fkc) , Tk(c) –
в середине; F(ike) , F(Fke) ,
Tk(e) – в конце интервала
(рис. 1 .2); Т0 – некото-
рое произвольное число. Матричная трактов-
ка формулы Симпсона (18.2) позволяет вычис-
лить перемещения от силового воздействия с любой предва- рительно заданной точностью.
В частном случае, когда Tk(s) = const = Tk, соотношение (18.2) перепишется:
1 |
l |
|
|
lk |
(F(в)F(в) |
|
|
F(е)F(е) )= F F+ |
||||||
òkFik (s)FFk (s)ds = |
+ 4 (с) |
(с) |
||||||||||||
|
Tk |
|
|
|
||||||||||
|
0 |
|
|
6T0 |
ik |
Fk |
ik |
Fk |
ik Fk |
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
FT |
P F= . |
|
|
|
|||
|
|
|
|
|
|
|
|
ik |
k |
Fk |
|
|
|
|
Так как T(в) |
= T(с) = T(е) |
= T , то приняв Т0 = Тk, в этом слу- |
|
|||||||||||
|
|
k |
k |
k |
|
|
|
k |
|
|
|
|
|
|
чае получим: |
|
|
|
|
|
|
é1 |
0 0ù |
|
|
|
|||
|
|
|
|
|
|
|
lk |
|
|
|
||||
|
|
|
|
P |
= |
|
ê0 |
4 |
0ú . |
|
|
|
||
|
|
|
|
|
6T |
|
|
|
||||||
|
|
|
|
k |
|
|
ê |
|
ú |
|
|
|
||
|
|
|
|
|
|
|
|
k |
ê |
0 |
ú |
|
|
|
|
|
|
|
|
|
|
|
|
ë0 |
1û |
|
|
|
|
Значение определённого интеграла (18.3) будет точным, если подынтегральная функция будет представлять собой ал- гебраический полином степени не выше третьей (например, когда определяются линейные и угловые перемещения от-
дельных сечений и узлов стержневых систем от силового воздействия, включающего сосредоточенные силы и момен- ты, а также равномерно распределённые нагрузки). Если же
силовое воздействие содержит распределённые нагрузки с
переменными интенсивностями, то матричная формулировка формулы Симпсона и в случае, когда Tk(s) = const даёт при-
ближённое значение определённого интеграла (1 .3).
18.3. Вычисление интегралов формулы Мора в матричной форме в случае линейных подынтегральных функций Фik(s), ФFk(s)
В п. 18.2 упоминалось, что численное значение опреде-
лённого интеграла (18.1) можно получить в матричной форме
(18.2)
lk F |
ik |
(s)F |
Fk |
(s)ds |
FТ P F= . |
|
ò |
|
|
|
|||
|
|
Tk (s) |
|
|||
0 |
|
|
|
ik k Fk |
||
|
|
|
|
|
|
|

Учитывая линейность функций Фik(s) и ФFk(s), их значе-
ния при s = |
0,5ℓk F(c) |
и F(c) |
выразим через F(в) |
и F(в) |
при |
||||
|
|
|
|
ik |
Fk |
ik |
Fk |
|
|
s = 0 |
и F |
(е) |
и F(е) |
при s = ℓk (рис. 1 .3). |
|
|
|||
|
|
ik |
|
Fk |
|
|
|
|
|
F(c) |
= 0,5(F(в) + F(е) ); |
|
|
|
|||||
ik |
|
|
ik |
ik |
|
|
|
|
|
|
F(c)Fk |
= |
|
|
|
|
|
|
|
0,5( (в) |
F+ F=(е) ). (1 .4) |
|
|
|
|||||
|
Fk |
|
|
Fk |
|
|
|
|
|
С учётом |
зависимо- |
|
|
|
|||||
стей |
(1 .4) |
матрицы |
|
|
|
||||
выражения (1 .2) FT |
|
|
|
|
|||||
и ФFk |
перепишутся: |
ik |
|
|
|
|
|||
]= |
|
|
|
||||||
ikT |
[Fik(в) Fik(c) Fik(e) |
|
|
|
|||||
[Fik(в)=Fik(e) ] |
é1 |
0,5 |
0ù |
|
|
|
|||
ê |
0,5 |
1 |
ú; |
|
|
|
|||
|
|
|
ë0 |
û |
|
|
|
||
|
éF(в) |
ù |
||
FFk |
ê |
Fk |
ú |
|
= êF(Fkc) |
ú |
|||
|
êF(e) |
ú |
||
|
ë |
Fk |
û |
|
é 1 |
0 |
ù |
éF |
|
ê |
|
ú |
||
ê0,5 |
0,5ú |
ê |
|
|
ê |
1 |
ú |
ëF |
|
ë 0 |
û |
|
|
|
=
(в) ù
Fk(e) ú .
Fk û
Принимая во внимание соотношения (1 .5), определён- ный интеграл выражения (1 .2) в матричной форме предста- вим следующим образом:
|
|
|
lk Fik (s)FFk (s)ds |
= |
|
|
|
|
|
|
|
||||||||
|
|
|
|
ò |
|
Tk (s) |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
é |
T0 |
|
|
|
|
|
ù |
|
|
|
|
|
|
|
|
|
|
|
|
ê |
|
0 |
0 |
ú |
|
|
|
|
|
|
|||
|
|
|
|
|
|
(в) |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
ê |
ú |
|
|
|
|
|
|
||||||
[F(в)=F(e) ]é1 |
0,5 |
0ù |
|
lk |
êTk |
T0 |
|
|
ú |
é 1 0 ù |
é |
|
(в) ù |
||||||
|
ê |
0 4 |
0 |
ú |
ê0,5 |
0,5ú |
êF Fk |
ú. |
|||||||||||
0,5 |
1ú |
|
6T |
|
|
||||||||||||||
ik ik |
ê0 |
|
ê |
|
|
T |
(c) |
|
|
ú |
ê |
ú |
ê |
F |
(e) |
ú |
|||
|
ë |
|
û |
0 |
|
|
|
k |
|
|
|
ê |
|
|
|
||||
|
|
|
|
|
|
ê |
|
|
|
|
|
ú |
ú ë |
|
Fk û |
||||
|
|
|
|
|
|
|
|
|
|
|
T0 |
ë 0 |
1 û |
|
|
|
|
||
|
|
|
|
|
|
ê |
0 |
|
0 |
|
ú |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
ê |
|
|
|
|
|
(e) ú |
|
|
|
|
|
|
|
|
|
|
|
|
|
ë |
|
|
|
|
|
Tk |
û |
|
|
|
|
|
|
Вычислив произведение трёх центральных матриц, получим:
|
|
|
|
|
|
lk F |
ik |
(s)F |
Fk |
(s)ds |
= |
|
|
|||||||||||
|
|
|
|
|
|
ò |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
Tk (s) |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
é |
T |
|
|
|
|
|
T |
|
|
|
|
|
T |
|
|
|
|
ù |
|
|
|
|
|
|
ê |
0 |
|
+ |
|
0 |
|
|
|
|
0 |
|
|
|
|
ú |
éF |
||||
|
|
l |
|
|
|
T(c) |
|
|
|
T(c) |
|
|||||||||||||
(в) (e) |
|
k |
êT(в) |
|
|
|
|
|
|
ú |
||||||||||||||
|
|
|
k |
|
|
|
|
|
k |
|
|
|
|
|
|
k |
|
|
|
|
|
ê |
||
[Fik =Fik |
] |
6T |
ê |
|
|
T |
|
|
|
T |
|
|
T |
|
ú |
êF |
||||||||
|
|
|
0 |
ê |
|
|
|
0 |
|
|
|
|
|
0 |
|
|
+ |
0 |
ú |
ë |
||||
|
|
|
|
|
|
(c) |
|
|
|
|
(c) |
|
|
|||||||||||
|
|
|
|
ê |
|
|
|
|
|
|
|
|
|
|
(e) |
ú |
|
|||||||
|
|
|
|
ë |
|
|
Tk |
|
|
|
Tk |
|
|
Tk |
|
û |
|
|||||||
(1 .6)
В формуле (1 .6):
|
|
|
é (в) |
FT |
= [F(в) F(e) ]; F = êF Fk |
||
ik |
ik ik |
Fk |
êF(e) |
|
|
|
ë Fk |
(в) ù
(e)Fk úú FTik Pk F=Fk . Fk û
ù
úú;
û
|
|
|
é |
T |
|
|
T |
|
|
|
|
ê |
0 |
|
+ |
0 |
|
|
l |
|
|
|
T(c) |
|||
Pk = |
k |
êT(в) |
|
|||||
|
ê |
k |
|
T0 |
|
k |
||
6T0 |
|
|||||||
|
ê |
|
|
|
|
|||
|
|
|
ê |
|
|
(c) |
|
|
|
|
|
ë |
|
Tk |
|
|
|
|
|
T0 |
|
|
ù |
|
|
|
|
|
ú |
|
T(c) |
||||
|
ú |
||||
T |
k |
T |
ú. |
||
0 |
|
|
0 |
ú |
|
(c) |
+ |
|
|||
|
(e) ú |
||||
Tk |
|
Tk |
û |
||
В случае, когда Tk(s) = const = Тk, т.е. когда T(в) = |
T(с) = |
k |
k |
= Tk(е) , при Т0 = Tk матрица Рk примет вид:
|
lk |
é2 |
1ù |
Pk = |
|
ê |
ú . |
|
|||
|
6Tk ë1 |
2û |
|
