
- •Предисловие
- •5. Работа внутренних сил плоской стержневой системы
- •6. Принцип возможных перемещений и упругие системы
- •9. Теорема о взаимности перемещений
- •10. Теорема о взаимности реакций
- •11. Теорема о взаимности реакций и перемещений
- •14. Теорема Лагранжа
- •18.1. Понятие о матрице перемещений
- •18.2. Вычисление интегралов формулы Мора в матричной форме в случае произвольных подынтегральных функций
- •18.4. Определение перемещений от силового воздействия
- •18.5. Определение перемещений от температурных воздействий
- •18.6. Определение перемещений от кинематических воздействий
- •1.7. Определение перемещений от совместных воздействий различного характера
- •5.1. РАСЧЕТ ОДНОПРОЛЕТНОЙ БАЛКИ
- •5.2. РАСЧЕТ ЛОМАНОГО БРУСА
- •5.3. РАСЧЕТ ТРЕХШАРНИРНОЙ РАМЫ
- •5.4. РАСЧЕТ ФЕРМЫ С ТРЕУГОЛЬНОЙ РЕШЕТКОЙ (АНАЛИТИЧЕСКИЙ СПОСОБ)
- •5.5. РАСЧЕТ ФЕРМЫ С ТРЕУГОЛЬНОЙ РЕШЕТКОЙ (ГРАФИЧЕСКИЙ СПОСОБ)
- •6.1. КИНЕМАТИЧЕСКИЙ АНАЛИЗ ЗАДАННОЙ РАСЧЕТНОЙ СХЕМЫ
- •6.2. ЗАМЕНЯЮЩАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ ЭЛЕМЕНТАРНЫХ РАСЧЕТНЫХ СХЕМ
- •6.3. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ
- •6.7. ПРОВЕРКА ПОЛУЧЕННОГО РЕШЕНИЯ ЗАДАЧИ
- •7.2. ПОСТРОЕНИЕ НАПРАВЛЯЮЩИХ ЭПЮР
- •7.3. РЕАЛИЗАЦИЯ МАТРИЧНОЙ ФОРМЫ ВЫЧИСЛЕНИЯ ПЕРЕМЕЩЕНИЙ
- •7.3.1. РАЗРАБОТКА СХЕМЫ ДИСКРЕТИЗАЦИИ
- •7.3.2. МАТРИЧНАЯ ФОРМА ПРЕДСТАВЛЕНИЯ ГРУЗОВОЙ И НАПРАВЛЯЮЩЕЙ ЭПЮР
- •7.3.3. ПОСТРОЕНИЕ МАТРИЦЫ ПОДАТЛИВОСТИ
- •7.3.4. ПРИЕМЫ МИНИМИЗАЦИИ РАЗМЕРОВ МАТРИЦЫ ПОДАТЛИВОСТИ
- •7.4. ПРОВЕРКА ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ
- •8.1. КИНЕМАТИЧЕСКИЙ АНАЛИЗ ЗАДАННОЙ РАСЧЕТНОЙ СХЕМЫ
- •8.2. КЛАССИФИКАЦИЯ СТЕРЖНЕЙ РЕШЕТКИ ФЕРМЫ
- •8.3. ОПРЕДЕЛЕНИЕ УСИЛИЙ В СТЕРЖНЯХ ГРАФИЧЕСКИМ СПОСОБОМ
- •8.5. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ НА ОСНОВЕ ЛИНИЙ ВЛИЯНИЯ
- •9.1. ПОСТАНОВКА ЗАДАЧИ РАСЧЕТА
- •9.3. ВЫБОР ОСНОВНОЙ СИСТЕМЫ МЕТОДА СИЛ
- •9.4. КАНОНИЧЕСКАЯ СИСТЕМА УРАВНЕНИЙ МЕТОДА СИЛ
- •9.5. МАТРИЧНАЯ ФОРМА МЕТОДА СИЛ
- •9.5.1. РАЗРАБОТКА СХЕМЫ ДИСКРЕТИЗАЦИИ
- •9.5.4. ФОРМИРОВАНИЕ КАНОНИЧЕСКОЙ СИСТЕМЫ УРАВНЕНИЙ
- •9.5.5. РЕШЕНИЕ КАНОНИЧЕСКОЙ СИСТЕМЫ УРАВНЕНИЙ
- •9.7. КОНТРОЛЬ ПРАВИЛЬНОСТИ РЕШЕНИЯ ЗАДАЧИ
- •10.1. ПОСТАНОВКА ЗАДАЧИ РАСЧЕТА
- •10.2. НАЗНАЧЕНИЕ СИСТЕМЫ ДОПОЛНИТЕЛЬНЫХ СВЯЗЕЙ ДЛЯ СОЗДАНИЯ ЗАМЕНЯЮЩЕЙ СИСТЕМЫ ОДНОПРОЛЕТНЫХ БАЛОК
- •10.3. ОСНОВНАЯ СИСТЕМА МЕТОДА ПЕРЕМЕЩЕНИЙ
- •10.4. КАНОНИЧЕСКАЯ СИСТЕМА УРАВНЕНИЙ МЕТОДА ПЕРЕМЕЩЕНИЙ
- •10.5 СТАНДАРТНЫЕ ЭПЮРЫ МЕТОДА ПЕРЕМЕЩЕНИЙ
- •10.6. ГРУЗОВАЯ И ЕДИНИЧНЫЕ ЭПЮРЫ МЕТОДА ПЕРЕМЕЩЕНИЙ
- •10.7. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ И СВОБОДНЫХ ЧЛЕНОВ КАНОНИЧЕСКОЙ СИСТЕМЫ УРАВНЕНИЙ МЕТОДА ПЕРЕМЕЩЕНИЙ
- •10.9. ОПРЕДЕЛЕНИЕ ОРДИНАТ ЭПЮРЫ ИЗГИБАЮЩЕГО МОМЕНТА В ЗАДАННОЙ РАСЧЕТНОЙ СХЕМЕ

С.Ф. ЗЛОБИН, Г.Н. ТЕЛИЧКО
СТРОИТЕЛЬНАЯ МЕХАНИКА
ОСНОВЫ ТЕОРИИ И РАСЧЁТА ПЛОСКИХ СТЕРЖНЕВЫХ СИСТЕМ
Издание четвертое, переработанное
Тула 2010
УДК 624.04
Злобин С.Ф., Теличко Г.Н. Строительная механика. Основы теории и расчёта плоских стержневых систем: Учебник. – Тула: Изд-во
.........., 2010. – .......... с.: ил.
ISBN ...................................
Учебник составлен ....
ISBN .................................... |
© Злобин С.Ф., Теличко Г.Н., 2010 |
ПРЕДИСЛОВИЕ
Строительная механика в вузе
Проблемы решениязадачСМ на ЭВМ
Строительная механика как учебная дисциплина от несена государственным образовательным стандартом 2000 года к специальным дисциплинам. Тем самым подчёркивается её базовая роль в подготовке дипломированных специалистов по направлению «Строительство», получающих квалификацию инженера в рамках образовательной программы «Промышленное и гражданское строительство».
Основной целью изучения этой учебной дисциплины является подготовка студентов к профессиональной деятельности в области общих методов расчёта строительных конструкций на прочность, жесткость, устойчивость
и колебания.
Сегодня реальная инженерная деятельность осущест вляется средствами программных комплексов автоматизированного расчёта на ЭВМ. Однако это не снимает с инженера ответственности за результаты расчёта, которые могут оказаться неверными по довольно большому перечню причин.
Например, достаточно много ошибок связано с неверной интерпретацией характера соединений конструктивных элементов в узлах, способов их опирания на землю, характера поведения под нагрузкой и т.п.
Не последнее место в этом перечне занимает неуме ние проводить контроль получаемых результатов по качественным характеристикам. В частности, речь идёт о характере распределения характеристик напряжённо-де- формированного состояния в элементах рассчитываемой конструкции.
Одним из серьёзных недостатков подготовки инжене ра может стать отсутствие навыков проведения оценки количественных результатов, получаемых с ЭВМ, на базе
3
Теоретические основы СМ и расчёты на ЭВМ
приближённого расчёта с использованием традиционных методов строительной механики.
Ксожалению, дажерекомендованнаяметодикапроведения расчётов в двух независимых программных комплексах типа Lira и SCAD не позволяет избежать серьёзных погрешностей, а порой и грубых ошибок при автоматизированном расчёте.
Поэтому для студентов остаётся актуальным изуче ние теоретических основ, лежащих в основе разработки расчётных схем реальных строительных конструкций, а также их расчёта классическими методами строительной
механики.
Анализ гипотез, лежащих в основе разработанных классических и численных методов расчёта, позволяет контролировать решения, принимаемые при формировании расчётной схемы для численного решения.
Классические же методы расчёта, обладая «прозрачностью» и сравнительно малой трудоёмкостью, позволяют получить навыки, необходимые для контроля результатов расчёта работы расчётной схемы под различными видами внешних воздействий, полученных численными методами современных САПР.
В настоящем учебнике представлены материалы, освещающие систему гипотез строительной механики и те орем, полученных на их основе, позволяющих обосновать классические методы (метод сечений, метод сил, метод перемещений и др.) и их современное воплощение в форме метода конечных элементов.
Рассматривается также методика решения классичес ких задач строительной механики средствами програм много комплекса SCAD, реализующего метод конечных элементов.
Авторы
4

Основы теории Часть1. плоских расчётных схем
Г Л А В А
1
НЕМНОГОИСТОРИИ
Строительная механика как теоретическая и прикладнаянаукавходитсоставнойчастьювразделестествознания, известный с древних времен под названием «Механика». Поэтому ее развитие неразрывно связано с другими областями механики (теоретической механикой, сопротивлением материалов, теорией упругости, теорией пластичности и ползучести).
Предметом же забот собственно строительной механики является определение усилий в элементах конструкции и перемещений ее отдельных точек от различных видов воздействий (силовых, кинематических, температурных). Следует подчеркнуть, что решая перечисленные выше задачи, строительная механика имеет дело не с реальной конструкцией, а с ее моделью, именуемой «расчётная схема».
Расчетная схема конструкции создается на основе целого ряда гипотез и соглашений, которые позволяют упростить изображение конструкции, описание ее механических свойств, своеобразие внешних воздействий, а также конструктивных особенностей.
Сегодня, изучая строительную механику, мы пользуемся устоявшейся системой принципов, гипотез и методов расчёта. Однако каждый принцип, каждая гипотеза и метод прошли определённый исторический путь развития.
Было время, когда в основе проектирования и возведения строительных сооружений решающее значение имел накопленный практический опыт. Однако со временем развитие механики и математики позволили построить достаточно изящное и эффективное здание науки, которая называется классической строительной механикой.
5

В этом здании и по сию пору трудятся многие специалисты, решая современные задачи проектирования зданий и сооружений.
Висторическом плане развитие механики как науки прошло несколько этапов.
1.1.Начальныйпериодразвитиямеханики
Вэтот период исследованию подвергаются лишь самые простые виды равновесия и движения материальных тел под действием простейших факторов: силы тяжести,
Особенности
начальногопериода
развитиямеханики
Роль опыта в проектировании
силы живой тяги и т.д.
Формирование научных абстракций механики находитсявзачаточномсостоянии. Сложностьзадачмеханики невыходитзаобластькомпетенцииэлементарнойгеометрии, арифметики и элементарной алгебры.
Уже египтяне использовали эмпирические связи между размерами сооружения и свойствами материала для него. В период между 2700 по 1680 гг. до н.э. в Египте сооружались пирамиды: самая большая из них достигала 147 м высоты и имела в основании квадрат со стороной
233 м.
Греки разработали статику, лежащую в основе механики материалов.
Так Архит Тарентский (первая половина IV в. до н. э.) – форулирует первые теории рычага, весов, винта, безмена, колеса, блока, клина на основе введения в математику механических методов, что впоследствии нашло продолжение в работах Архимеда.
Архимед(287-212 гг. дон.э.) далстрогоедоказательство условий равновесия рычага и указал методы отыска-
ния центров тяжести тел.
Римляне умели проектировать арки. До сих пор выполняет свои функции Гардский арочный мост в Южной Франции. Интересно отметить, что арки римлян были более лёгкими, нежели арки их предшественников. Однако опора только на накопленный практический опыт ограничивала использование арок небольшими пролётами и формой, близкой к окружности.
6

1.2. Развитиемеханикивсредниевека
Место
математики в механике
Эксперименты
Накопленный опыт греков и римлян был в своей значительной части утрачен в средние века. И только в эпоху Возрождения появились работы, которые продолжили
развитие механики как науки.
Особое место в этот период занимают исследования Леонардо да Винчи (1452-1519). Он не оставил после себя книг по механике. Однако в его записных книжках исследователи обнаружили массу записей, которые реализовали его пониманием механики как науки: «Механика – это рай математической науки, поскольку
мы получаем в ней плоды математики».
Леонардо да Винчи пользовался методом моментов, применял идею принципа возможных перемещений, имел, по-видимому, правильное представление о распоре в арке, пользовался правилом параллелограмма для сложения сил; экспериментально исследовал растяжение
вмеханике проволоки, изгиб балки, устойчивость колонн.
1.3.Механикавпериодновоговремени
Роль
доступности
информации
Правило
параллелограмма
сил
Указанные достижения да Винчи представляют собой, вероятно, первую попытку применения статики к определению сил, действующих на элементы строительных конструкций, а также первые опытные определения сопротивления строительных материалов. Но эти ценные научные открытия оставались погребенными в его записных книжках, и только в 1797 г. были частично обнародованы Вентурием.
Так что инженеры XV и XVI столетий продолжали, как и в римскую эпоху, назначать размеры элементов своих сооружений, полагаясь лишь на практический опыт
или на догадку.
Вместе с тем нидерландец Симон Стевин (1548-1620) в книге «Начала статики» (1586) изложил теорию рычага, равновесия тел на наклонной плоскости и гидростатику, что привело к открытию закона параллелограмма сил.
7
Гипотеза Галилея о распределении напряжений по поперечному сечению
Гипотеза Гука о линейной связи приложенныхсили мер искажений упругого тела
Законы
Ньютона
Первые попытки установления безопасных размеров элементовсооруженийаналитическимпутемотносятсяк
XVII веку.
Галио Галилей (1564-1642) в книге «Две новые науки» обосновывает некоторую систему анализа напряже ний, которые ему были известны. Эта книга фактически означала возникновение науки о прочности, т. е. сопро-
тивления материалов.
Интересно отметить, что, изучая изгиб балок, Галилей исходил из гипотезы о том, что напряжения во всех точках поперечного сечения балки являются положительными и одинаковыми по величине.
Совершенно новым понятием, к которому пришел Галилей, было понятие ускорения.
В 1678 г. вышла из печати работа Роберт Гука (16351703) «De potentia restitutiva or of spring» (О восстанови-
тельной способности или об упругости). В ней содержатся результаты проведенных Гуком опытов с упругими телами. Это был первый печатный труд, в котором рассмат-
ривались упругие свойства материалов.
На базе проведенных экспериментов Гук сформулировал положение, которое можно считать первой формулировкой закона Гука «Совершенно очевидно, что правилоилизаконприродыдлявсякогоупругоготеласостоитв том, что его сила или способность восстанавливать свое естественное состояние всегда пропорциональны той мере, на которую оно выведено из этого своего естественного состояния, совершено ли это путем его разрежения, отделения его частей одна от другой или же путем сгущения или уплотнения этих частей».
Такая формулировка закона (1660) долгое время (около 100 лет) оставляла место для различный интерпретаций свойства упругости: упругость как свойство материала и упругость как функция формы и размеров конструкции.
Гук также связал изгиб с растяжением волокон сечения на выпуклой стороне балки и их сжатием на вогнутой
стороне.
Исаак Ньютон (1642-1727) в своём главном научном труде «Математические начала натуральной философии
8
Предельные
нагрузки
Гипотеза
Мариотта о распределении напряжений по поперечному сечению
Гипотеза Я. Бернулли о поведении сечения балки
Связь
изгибающего
момента и кривизны
Формулировка
принципа
возможных
перемещений
(1687) сформулировал ряд основополагающих для механики понятий и формулировок:
1)Установление понятия массы.
2)Обобщение понятия силы.
3)Ясная и общая формулировка правила параллелограмма сил.
4)Установление принципа равенства действия и про-
тиводействия.
Эдм Мариотт (1620-1684) экспериментально исследовал предельные нагрузки для балок. Он установил, что такая нагрузка для защемлённой по концам балки вдвое больше, чем при шарнирном её опирании.
Мариотт считал, что в предельном состоянии положение нейтральной оси при изгибе не имеет существенного значения, и что усилия на вогнутой стороне сечения рав-
ны нулю.
В 1680 г. независимо от Гука он установил тот же самый закон. Он заметил, что сопротивление балки изгибу связано с растяжением и сжатием ее частей, так как некоторые продольные волокна оказываются растянутыми, а, некоторые – сжатыми. Он считал, что половина волокон
испытывает растяжение, а половина – сжатие.
Яков Бернулли (1654-1705) решал задачу вычисления прогиба балок, опираясь на гипотезу от том, что касательная к контуру поперечного сечения с вогнутой поверхности перпендикулярна к плоскости действия внешних
нагрузок.
В своей работе (1705) он получил уравнение, которое показывает, что кривизна кривой изгиба в каждой своей точке пропорциональна изгибающему моменту в этой же точке. Эта зависимость была принята впоследствии другими исследователями упругих линий изгиба (прежде
всего Эйлером).
Иоганн Бернулли (1667-1748), младший брат Якова Бернулли, автор формулировки принципа возможных перемещений (1717): работа всех сил, приложенных к системе, находящейся в равновесии, на совместных с наложенными на неё связями бесконечно малых перемещениях равна нулю.
9
Первый вариант уравнения колебаний бруса
Понятие сил инерции материальной частицы
Уравнение изгиба упругойлиниидля большихпрогибов
Уравнение
продольногоизгиба длямалыхпрогибов
Уравнение изгиба упругой линии длямалыхпрогибов
Сын И. Бернулли, Даниил Бернулли (1700-1772)
впервые вывел дифференциальное поперечных колебаний бруса призматического сечения. Это позволило ему исследовать частные случаи колебаний.
Леонард Эйлер (1707-1783) является учеником И. Бернулли, отца Николая и Даниила Бернулли. Степень магистра наук получил в возрасте 16 лет. Летом 1727 г. переехалвг. Петербург(Россия), гдев1730 г. сталчленом Российской Академии наук по разделу физики.
Интересно отметить, что только за период 1766-1783 гг. им было написано более 400 трудов! И даже после его смести Российская Академия ещё в течении 40 лет печа-
тала его работы.
В своей книге по механике, изданной в 1736 г., он впервые применил аналитические методы для вывода уравнений движения частицы и ввёл понятие сил инерции, а также показал, как интегрирование этих уравнений
позволяет выяснить движение тела в целом.
Для случая статического изгиба упругой линии (по теорииупругойкривойбрусмыслитсякаклинейнаясовокупность частиц, сопротивляющаяся изгибу) Эйлер вывел уравнение изгиба без использования гипотезы о малости прогибов, которое для малых прогибов вырождается
в уравнение Я. Бернулли.
Эйлер исследовал загружение упругой линии сжимающей силой, и для случая малого угла между направлением силы и осью искривлённой линии в точке приложе ния силы получил известное соотношение для критичес
кой силы P = C 2 4l 2 .
В отношении постоянной С Эйлер высказывал гипотезу, что для прямоугольной балки она пропорциональна ширине сечения и квадрату высоты. Впоследствии он исправил это предположение и стал считать жесткость при
изгибе пропорциональной четвёртой степени.
На базе гипотезы о малых поперечных перемещениях колеблющейся балки Эйлер сформулировал дифференциальное уравнение изогнутой оси балки в современной форме. При этом выводе он также пользовался положением, фактически соответствующим принципу Даламбера в его простейшем понимании.
10
Общие
уравнения
механики
Лагранжа
Множественность форм потери устойчивости
Гипотеза о положении нейтральной оси балки при изгибе
Лерон Даламбер (1717-1783) в книге «Трактат по динамике» сформулировал «принцип Даламбера», который позволял сводить задачи динамики твёрдых тел к статическим задачам.
В период 1759-1766 гг. Жозефом Луи Лагранжем
(1736-1813) была подготовлена книга «Аналитическая механика». В ней, пользуясь принципом Даламбера и началом возможных перемещений, он ввел понятия «обобщенных координат» и «обобщенных сил» и свел теорию механики к некоторым общим уравнениям, из которых стало возможным выводить все необходимые формулы
для решения тех или иных частных задач.
В руках Лагранжа механика превратилась в отрасль математическогоанализа, которуюонназвал«геометрией четырех измерений». В те времена лишь немногие были способны оценить такой способ трактовки механики, и Лагранжу пришлось испытать трудности, чтобы найти издателя для своей книги. В конце концов она была напечатана в Париже в 1788 г., сто лет спустя после того, как
вышли в свет «Начала» Ньютона.
Исследуя устойчивость упругой линии Лагранж показал, что при малых прогибах существует бесконечно многокривых, удовлетворяющимуравнениюпродольногоизгиба.
В XYIII веке наиболее активные научные исследования в области механики велись во Франции. Там же были выпущены первые печатные издания по строительной ме
ханике.
Задача изгиба балки, основанная на учёте положения нейтральной оси сечения, была решена Параном (16661716). Он исправил ошибку, допущенную Мариоттом при оценке распределения напряжений по поперечному сечению, и находил его из условия, что силы сопротивления, распределенные по сечению заделки, должны составлять систему сил, уравновешивающую внешнюю нагрузку. При этом он указывал, что возможно смещение нейтральной оси к сжатым волокнам сечения (в заделке балки) по мере приближения нагрузки к предельному значению.
Следующий шаг в развитии теории механики упругих тел был сделан Шарлем Огюстэном Кулоном (1736-
11
Гипотезы теории балок Кулона
Гипотеза Кулона о двух константах описания упругих свойствматериала
Гипотеза Кулона оприродезатухания колебаний
Модуль
упругости
Юнга
1806). Он рассмотрел изгиб балок с конечными размерами сечения.
Кулон принял во внимание как уравнение равновесия горизонтальных проекций всех сил, действующих на часть балки, отсекаемую одним из ее нормальных сечений, так и уравнение моментов. Благодаря этому он получил возможность найти истинное положение «нейтраль ной линии», или оси равновесия, и сделал верный под-
счет момента упругих сил.
Его теория балокявляетсянаиболее точнойиз тех, которые основаны на предположении, что напряжения в изогнутой балке зависят только от растяжения и сжатия ее продольных волокон и математически выводятся из этого допущения и из закона Гука. Он показал, что можно пренебрегать влиянием поперечных сил при изгибе балке, если высота сечения балки мала в сравнении с её дли-
ной.
Занимаясь исследованиями кручения в форме крутильныхколебаний, Кулонустановил, чтодлятого, чтобы характеризовать механические свойства материала, необходимы две численные характеристики, а именно: число m, определяющее упругое свойство материала, и число p,
указывающее предел упругости.
Исследуя затухание крутильных колебаний Кулон приходитквыводуотом, чтопричинойзатуханияявляется внутреннее несовершенство материала.
Наконец, Кулон, изучив разрушение сжатых элементов, приходит к выводу, что главной причиной разрушения является сдвиг. Такое предположение стало основой для построения одной из теорий прочности.
В 1800 г. английский ученый Томас Юнг (1773-1829) пришел к выводу, что если пользоваться не абсолютными значениями сил и смещений в конструкциях, а напряжениями и деформациями, то закон Гука можно записать в следующем виде:
----------------- -
Напряжение = const .
Деформация Юнг заключил, что эта константа является неотъем-
лемой характеристикой каждого материала и представляет его жесткость. Эта константа упругости называется те-
12
Гипотеза Юнга
одеформациях
поперечного
сечения бруса
Гипотеза Навье о существовании пределаупругости
Расчёт по упругому состоянию
перь модулем Юнга Е. Следовательно, Е описывает жесткость материала как такового. Жесткость же конструкции зависит не только от модуля Юнга материа-
ла, но и от геометрической формы конструкции.
Юнг заметил также, что сжатие бруса всегда сопровождаетсяегоутолщением, азначит, увеличениемплощади его поперечного сечения. Растяжение же делает брус или проволоку тоньше, следовательно, уменьшает площадь сечения.
В 1826 г. появилось первое печатное издание книги французского инженера и ученого Луи Мари Анри Навье (1785-1836) по сопротивлению материалов, содержащее главнейшие его открытия в этой области. Если сравнивать эту книгу с аналогичными сочинениями XVIII века, то ясно заметен большой сдвиг, который совершила механика материалов за первую четверть XIX века.
Инженеры XVIII века пользовались экспериментом и теорией с целью установления формул для вычисления предельных (разрушающих) нагрузок, Навье же с самого начала указывает, насколько важно знать предел, до которого сооружения ведут себя идеально упруго и не получа-
ют остаточных деформаций.
В пределах упругости деформацию можно считать пропорциональной силе и установить сравнительно простые формулы для вычисления ее величин. За пределом же упругости зависимость между силами и деформациями получается очень сложной и вывод простых формул для определения разрушающих нагрузок становится не-
возможным.
Навье полагает, что если применять формулы, выведенные для расчета по упругому состоянию существующих сооружений, обнаруживших свою достаточную прочность, то таким путем можно установить значения безопасных напряжений для различных материалов и в дальнейшем пользоваться этими данными при назначениинадлежащихразмероввпроектахновыхсооружений.
В первых двух главах своей книги автор исследует простое сжатие и простое растяжение призматического бруса, причем отмечает, что для полного описания механических свойств материала недостаточно дать только
13
Теория плоского изгиба бруса
Гипотеза плоских сечений Навье
Приближённая кривизнаосибалки прималыхпрогибах
Метод Навье решениястатически неопределимых задач
его предел прочности, но необходимо также установить и
его модуль упругости Е.
Третья глава посвящена изгибу призматического бруса, и здесь Навье с самого начала принимает, что изгиб происходит в той же самой плоскости, в которой действует нагрузка, в связи с чем его исследование может относиться лишь к балкам, имеющим плоскость симметрии и
нагруженным в ней же.
Полагая, что поперечные сечения остаются плоскими при изгибе, и применяя три уравнения статики, он заключает, что нейтральная линия проходит через центр тяжести поперечного сечения и что кривизна оси определяется уравнением EJ = M , где EJ является моментом инерции поперечного сечения относительно нейтральной ли-
нии.
Считая прогибы малыми и совмещая ось х с осью балки, он получает зависимость
1 |
d 2 y |
- = |
- |
---2 . |
|
|
d x |
Навье первый разработал общий метод решения ста- |
|
тически неопределенных задач в механике материалов. Он утверждает, что такие задачи представляются неопределенными лишь постольку поскольку телам приписывается абсолютная жесткость, но что, приняв во внимание их упругость, мы всегда имеем право присоединить к уравнениям статики еще некоторое число уравнений, выражающих условия деформации, так что в нашем распоряжении всегда окажется достаточное число зависимостей, чтобы найти все неизвестные величины.
В своей книге Навье внес много ценного в теорию изгиба кривого бруса. Уже Эйлер высказал гипотезу, что при изгибе первоначально искривленного бруса изгибающий момент пропорционален приращению кривизны. Навье принимает формулу
EJ 1 – 1 = M
- --
0
и использует ее для исследования изгиба кривого бруса, заделанного одним концом. Навье вычисляет распор Н для параболических и круговых арок.
14
Гипотеза Навье о природе сил упругости
Понятия
нормального и касательного напряженийКоши
Виды малых деформаций
В начале XIX века были предприняты попытки подвести под механику упругого тела более глубокое обосно вание. ЕщёсовремениНьютонасуществовалоубеждение в том, что свойство упругости тел может быть объяснено силами притяжения и отталкивания, действующими меж-
ду мельчайшими частицами этих тел.
Навье сделал также следующий шаг в молекулярной теории упругого тела. Он вводит предположение, что на каждую частицу упругого тела действуют две системы
сил F и F1 . Силы F1 уравновешивают друг дру-
га и представляют собой молекулярные взаимодействия, обнаруживающиеся при отсутствии внешних сил. Силы
же F1 уравновешивают внешние силы, к которым от-
носится, например, сила тяжести. В отношении их вводится предположение, что они пропорциональны изменениям расстояний между частицами и действуют по соеди няющим их прямым.
Присоединяя к внешним силам силу инерции частицы, Навьесформулировалобщиеуравнениядвиженияупругого тела (1821) с одной постоянной, характеризующей
свойство упругости материала.
Теорию упругости Навье развил французский ученый Огюстен Луи Коши (1789-1857). Коши принадлежит гипотеза о том, что давление на любую поверхность твердого тела, в том числе и на плоскость внутри тела, не обязательно должно быть ей перпендикулярным. Это позволило ему ввести понятия нормального и касательного напряжений и установить точное число разного вида напряжений, котороенеобходимодляполнойхарактеристики механического состояния любой напряжённой плос-
кой поверхности внутри тела.
Коши исследует также и возможные в области точки деформации упругого тела и показывает, что если эти деформации малы, то относительное удлинение в какомлибо направлении и изменение прямого угла между двумя произвольными, первоначально взаимно-перпендику- лярными, направлениями могут быть выражены через шесть компонент деформации: три линейные деформа-
15
Гипотеза Коши о линейной связи напряжений и малых деформаций
Кручение и гипотеза плоских сечений
Коэффициент
Пуассона
ГипотезаПуассона о несжимаемости материала
ции по координатным осям и три угловые деформации, т.
е. искажения углов между этими осями.
Коши дает, сверх того, и соотношения между шестью компонентами напряжения и шестью компонентами деформации для изотропного тела. Допуская, что главные направления деформации совпадают с направлениями главных напряжений и что доставляющие напряжений являютсялинейнымифункциямикомпонентдеформации, он пишет уравнения полной системы уравнений для решения задач упругости изотропных тел с двумя постоян-
ными, характеризующими упругие свойства материала. Используя эту систему он показывает, что попереч-
ные сечения стержня, подвергающегося кручению, как правило, не остаются плоскими.
Немногим позже уравнениями равновесия занялся современник Навье и Коши, их соотечественник Симеон Дени Пуассон (1781-1840). В механике, кроме уравнений равновесия, колебаний и прогиба стержней, изгиба круглых пластинок и других задач, Пуассон оставил память о
себе тем, что ввел коэффициент, получивший его имя. Еще Юнг отметил, что при сжатии стержня попереч-
ное сечение элемента увеличивается, а при растяжении – уменьшается. Так вот, отношение упругого уменьшения или увеличения поперечного размера элемента к его продольному удлинению или укорочению является величи-
ной, постоянная для каждого материала.
Пуассон исходил из того, что объем элемента до приложения нагрузки и после этого не изменяется. Изменяется лишь форма. В частности, при сжатии стержня увеличивается его площадь сечения и уменьшается высота. При растяжении, наоборот, уменьшается площадь сечения и увеличивается высота. При таком подходе влияние материала не учитывалось, считалось, что он не играет роли. Поэтому коэффициент Пуассона был величиной постоянной для любого материала, равной 0,25.
В дальнейшем величина и универсальность коэффициента Пуассона подверглись сомнению.
Пуассон выводит уравнения для продольных, крутильных и поперечных колебаний стержней и вычисляет частоты для различных форм колебаний.
16
Уравнения
прогибов и колебаний, основанные на гипотезе
плоских сечений
Применение тригонометрического ряда для решения уравнения изгиба
Два подхода к выводу уравнений упругости
В своем «Трактате по механике» Пуассон не пользуется общими уравнениями теории упругости, а выводит особые уравнения для прогибов и колебаний стержней, исходя из допущения, что в процессе деформирования поперечные сечения их остаются плоскими. Для изгиба призматических стержней он пользуется не только уравнением второго порядка, выражающим пропорциональность кривизны упругой линии изгибающему моменту, но также и уравнением
EJ d 4 y = q ,
----
d x4
где EJ – жесткость при изгибе, a q – интенсивность поперечной нагрузки. Рассматривая различные применения этого уравнения, Пуассон обращает внимание на любопытное его свойство: если q является функцией х, обращающейся в нуль на концах х = 0 и х = 1 стержня, то q всегда можно представить в виде синусоидального ряда.
По-видимому, здесь мы впервые встречаемся со случаем использования тригонометрического ряда для иссле дования кривых прогиба стержней. Однако во времена Пуассона этот метод не привлек к себе внимания инжене ров.
Оба этих выдающихся инженера – Габриэль Ламе
(1795-1870) и Бенуа Поль Эмиль Клапейрон (17991864) – окончили Политехническую школу в 1818 г. и Школу горных инженеров в 1820 г. во Франции. В течение последующих 11 лет работали в России (Институт
инженеров путей сообщения, г. Петербург).
В заключительных главах своей книги Ламе подвергает критическому анализу принципы, на основе которых строится вывод основных уравнений теории упру гости. Теперь он уже не одобряет вывод уравнений по способу Навье (с привлечением гипотезы молекулярных сил), а отдает предпочтение методу Коши (в котором используется лишь статика твердого тела). Затем он принимает гипотезу Коши, согласно которой компоненты напряжения должны быть линейными функциями компо нент деформации.
17
Две константы упругости Ляме
Первый вариант уравнения 3-х моментов
Теорема
Клапейрона о работе внешних сил
Первые исследования по кинематическому анализу
Мгновенная и геометрическая изменяемость
Для изотропных материалов принятие этой гипотезы приводитксокращениючисланеобходимыхупругихпостоянных до двух, находимых из испытаний на простое растяжение и простое кручение. Таким путем все необходимые уравнения получаются без обращения к каким либо гипотезам, относящимся к молекулярной структуре
или молекулярным силам.
Очередной шаг в развитии теории неразрезных балок был сделан Клапейроном. Он использует выражения для углов, образуемых в опорных точках касательными к изогнутой оси балки с первоначально горизонтальным ее направлением. И фактически получил уравнение 3-х моментов, но с ограничениями: пролёты балки одинаковы, а нагрузка является распределённой с одинаковой интен-
сивностью по всей длине балки.
Клапейрон сформулировал также теорему, согласно которой сумма произведений приложенных к телу внешних сил на компоненты смещений по направлениям этих сил в точках их приложения равна удвоенному значению соответствующей энергии деформации тела. Повидимому, эта теорема была сформулирована Клапейроном за много времени до выхода в свет книги Ламе, и ею, вероятно, отмечается первый случай вывода общего выражения для энергии деформации изотропного тела.
Несколько теорем, имеющих фундаментальное значение в теории ферм, было сформулировано А.Ф. Мёбиусом (1790-1868), профессором астрономии Лейпцигского
университета.
В своем учебнике статики Мёбиус рассматривает задачу равновесия системы стержней, соединенных между собой шарнирами, и показывает, что если общее число шарниров в такой системе равно n, то для получения из соединяющих эти шарниры стержней жесткой неизменя емой системы нужно иметь не менее 2n-3 стержней в плоской системе и не менее 3n-6 стержней в случае про-
странственной системы.
При этом Мёбиус указывает и на возможность исключительных случаев, когда система с 2n-3 стержнями может оказаться не абсолютно жесткой, допуская возможность малых относительных перемещений шарниров. Ис-
18
Метод нулевой нагрузки кинематического анализа
Статическая
определимость плоских ферм
Метод замены связей для расчёта ферм
следуя подобные исключительные случаи, он находит, что детерминант системы уравнений равновесия для уз лов таких ферм обращается в нуль. Отсюда он заключает, что если из системы, обладающей числом стержней, необходимым для того, чтобы она была жесткой, устранить один из этих стержней, то система будет допускать движение оставшихся в составе ее стержней, как механизм.
Важная работа Мёбиуса оставалась неизвестной инженерам на протяжении многих лет, и только когда практика освоила использование стальных ферм и когда в свя зи с этим потребовалось усовершенствовать общую их
теорию, инженеры вновь открыли теоремы Мёбиуса. Он указал также полезный практический прием реше-
ния вопроса о том, является данная система жесткой или нет. Если для какого-либо загружения мы можем найти усилия во всех элементах системы, не приходя к неопределенностям, то упомянутый детерминант получается отличным от нуля и система неизменяема. В качестве простейшего предположения Мёбиус допускает загружение нулевыми силами, и если при этом ни в одном из стержней усилие не отлично от нуля, мы вправе утверждать,
что система жесткая.
Мёбиус исследовал весьма важную задачу о самоуравновешивающейся пространственной стержневой системе в виде замкнутого многогранника и показал, что если плоские грани такого многогранника являются треугольниками или составлены из треугольников, то число стержней в ней в точности равно числу уравнений стати-
ки и такая система статически определима.
Работа Мёбиуса по пространственным системам также осталась неизвестной инженерам, и они впоследствии разработали теорию такого вида ферм независимо от Мё-
биуса.
Общий метод исследования сложных стержневых систем ферм был разработан Л. Хеннебергом. Метод основывается на возможности преобразования данной сложнойстержневойсистемывболеепростуюпутемудаления из нее некоторых стержней и замены их другими стержнями, иначе расположенными (1886).
19
Точность гипотез
оплоскомсечении
иненадавливании волокон друг
надругаприизгибе
Большие прогибы бруса
Принцип Сен-Венана
Уточнение теории изгиба кривого бруса
Французский ученый Адемар Жан Клод Барре Сен-
Венан (1797-1886) первый исследовал точность допущений, лежащих в основе теории изгиба:
1)поперечные сечения балки остаются при ее деформировании плоскими;
2)продольные волокна балки при этом не оказывают давления друг на друга, находясь в состоянии простого осевого растяжения или сжатия.
Он доказывает, что оба эти допущения строго выполняются лишь в случае чистого изгиба, когда на балку действуют две равные, противоположно направленные пары сил, приложенные по концам.
Впервые были установлены причины искажения первоначально прямоугольного поперечного сечения: под воздействием поперечного сужения волокон на выпуклой грани и расширения их на вогнутой, первоначально прямые линии верхней и нижней границы сечения искривля-
ются.
Сен-Венан исследует также большие прогибы консоли, при которых кривизна не может быть заменена приближенным значением второй производной от прогиба. Он дает решение в виде ряда, суммирование которого
позволяет вычислить прогиб любой желаемой точностью. При обсуждении чистого изгиба балок Сен-Венан
формулирует принцип, носящий ныне его имя. Он утверждает, что распределение напряжений, найденное для этого случая, совпадает с точным решением лишь при условии, если приложенные по концам внешние силы распределены по торцовым сечениям точно таким же обра зом, как они распределены и по промежуточным сечениям. Но полученное решение, как он утверждает, будет также достаточно точным и для всякого иного, если только равнодействующая сила и равнодействующая пара приложенных сил остаются неизменными при всех этих
распределениях.
Сен-Венан исследовал также изгиб кривого бруса, причем ввел в формулы Навье дополнительные члены, учитывающие перемещения, вызываемые удлинением оси бруса, а также сдвигом.
20
Сент-Венан изобрёл также полуобратный метод решения задач, который носит его имя. Метод основан на следующих рассуждениях: многие из обычных допущений и выводов, оказываются верными, по крайней мере, в большинстве случаев; следовательно, сохраняя некоторые из этих допущений и выводов, можно упростить уравнения и получить их решения; правда, пользуясь этими решениями, мы не можем удовлетворить любым напередзаданнымграничнымусловиям; однакожеграничные условия практически наиболее важного типа могут быть
удовлетворены.
Теория кручения Первой проблемой, к которой Сен-Венан приложил Сен-Венана свойметод, былапроблемакрученияпризматическихтел; соответствующуютеорию он далвзнаменитом мемуарео
кручении, относящемся к 1855 г.
Для получения решения он предположил, что деформация, с одной стороны, состоит, как и в теории Кулона, из простого закручивания вокруг оси призмы, а с другой стороны, – из деформации, выражающейся в смещениях, вдоль оси призмы, различных в различных точках поперечного сечения.
Эффект этих продольных смещений состоит в искривлении плоскостей поперечных сечений призмы, которые в результате деформации обращаются в изогнутые поверхности. Он показал, что такая деформация может поддерживаться в призме силами, приложенными только на ее концах.
Строгое решение задачи о касательных напряжениях в балках также было дано Сен-Венаном в его знаменитой работе об изгибах. Но в ней рассмотрено лишь небольшое число простейших поперечных сечений балок, и потому в более сложных случаях инженеры оказались вынужденными (как и по сей день) пользоваться приближенным элементарным решением, предложенным
Дмитрием Ивановичем Журавским (1821-1891).
Теория касательных напряжений в балках прямоугольного профиля была разработана Д. И. Журавским в 1844-1850 гг. в связи с проектированием деревянных мостов для железной дороги, соединявшей Петербург с Москвой.
21
Связь
изгибающего
момента ипоперечнойсилы
Расчёт по методу составных ферм
Метод сквозных сечений для расчёта плоских ферм
Теория расчёта арок
Принцип
наложения
воздействий
Дальнейшим прогрессом в расчете ферм мы обязаны
двум немецким инженерам: И. Шведлеру и А. Риттеру. Шведлер пользуется в своем анализе понятиями изги-
бающего момента и поперечной или перерезывающей силы и устанавливает соотношение Q = dM/dx, получившее в дальнейшем широкое применение в расчетах ферм.
Пользуясь этим уравнением, Шведлер показывает, что сечение, в котором изгибающий момент достигает своего максимального значения, является в то же самое время и тем сечением, в котором поперечная сила меняет знак. Рассматривая ферму с треугольной решёткой и рассекая ее сквозным поперечным сечением Шведлер находит усилия в трех перерезанных этим сечением элемен-
тах из трех уравнений статики.
Переходя к фермам с более сложной структурой решётки, он указывает, что при выполнении расчета их
следует разлагать на простые составляющие системы. Риттер упростил вычисление усилий в стержнях, пе-
ререзываемых сечением сквозным поперечным сечением, составляя и решая уравнения моментов относительно точек пересечения каждых двух из трех пересекаемых стержней. При этом для того, чтобы получить очень простые формулы для усилий в стержнях, нам приходится решать каждый раз лишь одно уравнение с одним неизвестным.
Жак Антуан Шарль Бресс (1822 -1883) родился во
Вьенне (Франция).
Главным достижением Бресса в инженерной науке была его теория кривого бруса с ее применениями в проектировании арок. Бресс не только дает общее решение задачи расчета арки, но и подробно исследует различные
частные случаи ее нагружения.
Здесь он приводит чрезвычайно важные соображения о принципе наложения и показывает, что для малых деформаций, следующих закону Гука, перемещения являются линейными функциями внешних нагрузок и могут бытьполученысуммированиемперемещений, вызванных отдельными частными нагрузками. В случае вертикальных нагрузок поэтому достаточно установить сначала эффект одной единичной вертикальной силы.
22
Развитие
теориинеразрезных
балок
Задача о невыгодном положениинагрузки
Понятие
фокусных
отношений
Графические
методы в статике
Третий том учебного курса Бресса содержит весьма подробное изложение теории неразрезных балок. В первой главе эта задача ставится в общем виде, и если Клапейрон и Берто требовали, чтобы все пролеты были одинаковыми, а нагрузка была распределена равномерно по всей длине балки, то Бресс отбрасывает эти ограничительные условия. Далее, он допускает, что опоры расположены не на одном уровне, и получает таким путем
уравнение трех моментов в его общей форме. Приложенные нагрузки Бресс делит на две группы: 1)
равномерно распределенная постоянная нагрузка, к которой относится собственный вес балки, и 2) подвижная нагрузка, которая может занимать лишь часть всей длины балки. Опорные моменты, вызванные постоянной нагрузкой, находятся путем решения уравнений трех моментов. Что касается подвижной нагрузки, то основная задача здесь заключается в том, чтобы найти для нее невыгоднейшееположениедлякаждогопоперечногосечениябал-
ки.
Бресс рассматривает случай одной сосредоточенной силы и обнаруживает при этом существование двух постоянных точек в ненагруженных пролетах (фокусов), являющихся точками перегиба упругой линии балки, когда единичная нагрузка размещается вправо или влево от одной из них.
Имея эти точки, мы получаем возможность построить эпюруизгибающихмоментовдлялюбогоположенияединичной сосредоточенной нагрузки, а из нее установить и наиболее неблагоприятное положение заданной подвижной нагрузки. Мы видим, что в этом исследовании Бресс
весьма близко подошел к идее линий влияния.
Карл Кульман (1821-1881) систематически провел использование графических методов для расчетов конс трукций всевозможных типов и составил первое руко водство по графической статике.
Применяя графический способ в исследовании статически определимых ферм, Кульман пользуется методом сечений, показывая, что если одновременно рассечь не более чем три стержня, то при этом всегда имеется возможность без труда получить значения усилий в этих
23
стержнях путем разложения известных внешних сил по направлениям этих стержней. Он строит также диаграммы внутренних усилий в фермах, исходя из условий равновесия в каждом из последовательных узлов и вычерчи вая соответствующие многоугольники сил.
Метод построения диаграмм сил, позволяющий каждую силу в том или ином элементе изобразить всегда од ной, был найден независимо двумя учеными: Джемсом
К. Максвеллом (1831-1879) и У. Тэйлором.
Теорема В своей работе по прогибам ферм Максвелл открыл
овзаимности существование весьма важного соотношения между про- Максвелла гибами, вызываемыми в ферме двумя различными вида-
Количественная
сторона
кинематического
анализа
Метод
возможных перемещений для расчёта ферм
Вычисление прогибов балок
ми нагрузок: если нагрузку, приложенную в узле В, перенести в узел А, то прогиб, который в нервом положении нагрузки получается в узле А, во втором ее положении будет наблюдаться в узле В.
К этому сводится содержание теории взаимности в той ее простейшей форме, в которой она была получена Максвеллом. В последующем эта теория была обобщена и стала весьма важным орудием в исследовании статически неопределимых систем.
 1864 г. он впервые предложит канонические уравнения метода сил для расчёта статически неопределимых шарнирных ферм.
В работе повторного открытия ряда забытых достижений механики выдающаяся роль принадлежит Отто
Мору (1835-1918).
Он установил требование, относящееся к числу стержней, необходимому для того, чтобы образовать жесткуюстатическиопределимуюсистему, исследовавтакже и исключительный случай бесконечно малой подвижнос-
ти.
Им доказано, что существуют статически определимые фермы, не поддающиеся расчету ранее указанными методами, и предложил для решения таких систем поль-
зоваться методом возможных перемещений.
Мор показал также, что прогибы балки могут быть вычислены как изгибающие моменты, вызванные в балке фиктивной нагрузкой интенсивностью M/EI, что чрезвычайно упрощает задачу определения прогибов.
24
Понятие линии влияния прогибов
Графический метод решения уравнения 3-х моментов
Влияние кривизны бруса не способ его исследования
Понятие линиивлияниясил
Сравнение
графических и аналитических методов расчёта
Мор ввёл понятие линии влияния прогиба в точке балки и, пользуясь принципом наложения, показывает, что если на балку действует несколько нагрузок
P1 P2 P3 ,..., a y1 y2 y3 являются соответствующими ординатами линии влияния, то прогиб в точке, производимый всеми этими нагрузками, равен Pi yi .
i
Это – первый случай применения линий влияния в инженерных расчетах. В статье 1868 г., Мор останавливается и на расчете неразрезных балок, причем предлагает
графическое решение уравнений трех моментов. Наиболее ценным вкладом Э. Винклера (1835-1888)
в сопротивление материалов была его теория изгиба кривого бруса. Навье и Бресс вычисляли прогибы и напряженияêривого бруса по формулам, выведеннымдля призматического бруса. Между тем, подобный подход к решению задачи законен лишь в том случае, если размеры поперечного сечения бруса малы в сравнении с радиусом кривизны его оси.
Винклер пытался вывести формулы сопротивления материалов, не пользуясь гипотезой плоских сечений, а основывая свои выводы на уравнениях точной теории. Впоследствии такой метод изложения сопротивления материалов вышел из употребления, и ныне принято вести
преподавание этой науки на более элементарном уровне. Винклер ввёл понятие линий влияния сил и пользо-
вался им при изложении теории расчёта мостов. В этой же книге он также обсуждал вопрос о возможностях гра-
фических и численных методов.
Он указывает, что за графическими методами нужно признать преимущества их большей наглядности и то, что они легче позволяют обнаруживать ошибки в вычислениях. Графические построения не так утомительны, как аналитические вычисления, и решения графическим путем получаются обычно за более короткий срок в сравнении с тем, который требуется для вычислений; результаты же их обеспечивают точность, достаточную для всех практических целей.
Но некоторые преимущества Винклер признавал и за численными методами: им следует отдавать предпочте-
25
Принцип
минимума
работ
Первая теорема Кастильяно
Вторая теорема Кастильяно
Линейная связь нагрузки и перемещений
Решение точногоуравнения продольногоизгиба
ние в тех случаях, где требуется более высокая точность и, в особенности, если для подобных расчетов уже составлены таблицы, предназначенные для разнообразных
применений.
Итальянский инженер Альберто Кастильяно (18471884) сформулирован принцип минимума работ (1773), который получил признание в качество одного из краеугольных камней теории сооружений. К своей теории Кастильяно приходит из исследования ферм с идеальными
шарнирами.
В соответствии с его первой теоремой линейные функции, получаемые нами в результате дифференцирования потенциальной энергии деформации по перемещениям, являются не чем иным, как соответствующими внешними
силами.
Согласно второй теореме Кастильяно, если энергия деформации представлена как функция независимых внешних сил, то производная этой функции по любой из этих сил дает соответствующее перемещение точки приложе-
ния силы в направлении силы.
Эти результаты, полученные Кастильяно первоначально для шарнирных ферм, в дальнейшем были им обобщены на упругое тело любого вида. Он выводит выражения упругой энергии для стержней, подвергающихся различным видам деформирования, и пользуется этими выражениями в разнообразных применениях своей теории для решения различных статически неопределенных задач о балках и арках. Однако для всех случаев применения Кастильяно исходил из того, что перемещения явля-
ются линейными функциями внешних сил.
Феликс Станиславович Ясинский (1856-1899) ро-
дился в Варшаве в польской семье. Ясинский исследовал решение точного дифференциального уравнения продольного изгиба призматического стержня и показал, что это решение приводит к тому же самому значению критической нагрузки, к которому пришел Эйлер из приближенного уравнения.
Ясинский не ограничился только теоретическим изучением продольного изгиба стержней, а, воспользовавшись результатами экспериментов Баушингера, Тетмайе-
26
Расширение числа вариантов опирания сжатых стержней
Устойчивость
составных
стержней
Учёт поперечной силы
Метод
последовательных
приближений для определения критической нагрузки
Применение
понятий обобщённых сил и обобщённых координат
ра и Консидера, составил таблицу критических значений
напряжений сжатия для различных гибкостей.
Он показал также, каким образом таблицу, составленную для сжатых стержней с шарнирными концами, можно применить и к другим случаям продольного изгиба, если ввести для этой цели понятие «приведенной длины»
стержня.
Другим инженером, внесшим много ценного в теорию продольного изгиба в рассматриваемый нами период, был Фридрих Энгессер (1848-1931). Энгессер первый занялся теорией продольного изгиба составных ко-
лонн.
Он исследовал влияние поперечной силы на величину критической нагрузки и нашел, что для сплошных колонн это влияние мало и им можно пренебречь, в сквозных же или в составных стойках оно может оказаться практически значительным, в особенности если ветви таких стоек или колонн соединить между собой одними лишь планками.
Энгессер вывел формулы для определения того отношения, в котором в каждом частном случае следует уменьшать значения эйлеровой критической нагрузки,
чтобы учесть гибкость элементов решетки.
Строгие решения дифференциального уравнения продольного изгиба известны лишь для простейших задач. Поэтому инженерам приходится часто довольствоваться лишь приближенными решениями. Идя навстречу такого рода запросам, Энгессер предложил метод вычисления критических нагрузок способом последовательных приближений. Чтобы получить приближенное решение, он рекомендует задаться некоторой формой изогнутой кри-
вой, удовлетворяющей граничным условиям.
Лорд Рэлей (Джон Уилльям Стрэтт, 1842-1919) Главный вклад Рэлея в науку содержится в его книге «Теория звука». Впервомтомеэтойзамечательнойкнигиисследуются колебания струн, стержней, мембран, пластинок и оболочек. Автор демонстрирует те преимущества, которые может извлечь инженер из применения понятий обобщенных сил и обобщенных координат. Введение этих понятий и использование теоремы взаимности Бет
27
Использование
приближённых форм колебаний
Проблемырасчёта рамных систем
Учёт смещений
иповоротов узлов рам
Гипотеза Мора о влиянии жёсткости узлов наихперемещения
ти-Рэлея внесло большое упрощение в расчеты статичес-
ки неопределимых систем.
Определяя частоты колебаний сложных систем, он приходиткприближенномурешению, задаваясьподходящей формой для заданного типа колебаний и приводя таким путем поставленную задачу к исследованию колебаний системы с одной степенью свободы. Затем он описывает те приемы, которыми можно повысить точность приближенного решения.
В XIX веке развитие теории сооружений определялось главным образом задачами расчета ферм. Достаточно приемлемые решения здесь могли быть получены, исходя из допущения, что узлы фермы шарнирные и, следовательно, все стержни подвергаются действию лишь
осевых усилий.
Внедрение в строительную технику железобетона сопровождалось широким использованием различных типов рамных систем, конструкций с жесткими узлами. Эти конструкции отличаются, как правило, высокой степенью статической неопределимости, и составляющие их эле-
менты работают главным образом на изгиб. Разработанные ранее методы обнаружили вскоре в
применении к такого рода системам свою несостоятельность и взамен их в практику проектирования вошли новые методы, основанные на учете деформаций. Поэтому в 1880 г. немецким инженером Мандлеров было выполнено исследование, в котором автор показывает, что в фермах с жесткими узлами нужно исследовать не только перемещения узлов, но и их повороты, и с этой целью выводит три необходимых уравнения равновесия для каждого узла.
Поскольку им учитывается при этом влияние осевых усилий на изгибающие моменты в стержнях фермы, его система уравнений получается весьма сложной и практи-
чески непригодной в применениях.
В 1892 г. О. Мор в рамках гипотезы о тем, что на перемещениях узлов их жесткость сказывается незначительно, и, основываясь на этом, определяет эти перемещения по методу, принятому для ферм с идеальными шарнирами. В качестве неизвестных величин он прини-
28

Гипотеза
Бендиксена овлияниилинейных смещений жестких узлов
Введение угловых связей взаданнуюсистему
мает углы поворота жестких узлов. Из условий равновесия узлов получается столько же уравнений сколько у нас имеется неизвестных поворотов. Хотя число уравнений может оказаться и значительным, все же они, как показывает Мор, легко решаются методом последовательных
приближений.
Систематическое использование углов поворота в расчете рамных систем было введено Акселем Бендиксеном (1914, Германия), разработавшим так называемый метод угловых деформаций, исходя из гипотезы о том, что линейными смещениями узлов рам можно пре-
небречь.
Следующий шаг в упрощении расчета стержневых систем был сделан К. А. Чалышевым (1922), который вычисляет моменты в узлах рамной системы в предположении, что узлы закреплены от поворотов, определяя, таким образом, неуравновешенные моменты в узлах рамы.
Окончательные значения концевых моментов получаются суммированием концевых моменты, произведенные неуравновешенными моментами в узлах, и предварительно вычисленных концевых моментов от нагрузки (способом последовательных приближений).
1.4.Строительнаямеханикавновейшеевремя
Впериод новейшего времени сведения об истории дальнейшего развития строительной механики можно по черпнуть из работ [2-3], [5], [12] и [13].
Подробное изложение достижений российских и советских учёных в этот период можно прочитать в книгах «Строительная механика в СССР. 1917-1957» (М.: Госстройиздат, 1957) и «Строительная механика в СССР. 19171967 (М.: Стройзидат, 1969).
Современный период развития строительного проектирования характеризуется переходом к использованию в расчётахэлектронно-вычислительныхмашин, выполняющих не только сложные численные процессы, но и логические функции: запоминание, отбор, классификация, решение уравнений, конструирование и моделирование,
29
контроль и экспертиза и т.д. Процесс этот развивается и находит своё воплощение в системах автоматизированного расчёте и проектирования строительных сооружений и конструкций.
Механика, в числе и строительная, также переходит в новую фазу развития. Бурно продолжается процесс выделения отдельных механических дисциплин и, соответственно, расширяется круг механических абстракций. Появляются такие понятия, как сжимаемые и пластичные, вязкие и разносопротивляющиеся материалы, и др.
Кроме основных принципов классической механики вводятся новые гипотезы о свойствах движения материальных тел, учитывающие физические, химические и другие процессы, происходящие в изучаемых телах и влияющие на их напряжённо-деформированное состояние.
30
Г Л А В А
2
МОДЕЛИРОВАНИЕ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ
Расчётная схема как модель сооружения
Упругая линия – базовый элемент расчётной схемы
Свойства плоской расчётной схемы
Как следует из анализа истории развития строительной механики, её развитие основано на введении достаточно большого количества разного рода гипотез, которые порождают некоторую модель сооружения, именуемую далее «расчётная схема».
Система этих гипотез не свободна от противоречий, тем не менее она обеспечивает достаточную точность решения задач о прочности, устойчивости и жёсткости для широкого круга строительных сооружений и конструкций.
В классической строительной механике стержневых систем базовым элементом расчётной схемы является отрезок прямой (или кривой), который наделяется рядом
идеализированных свойств.
Важнейшим из них является способность отрезка при определённых условиях сопротивляться внешним воздействиям за счёт изменения формы и размеров, т.е. за счёт деформирования. При этом важно отметить, что при удалении нагрузки происходит восстановление и формы, и размеров. Такие свойства ассоциируются с понятием «упругая линия».
Рассмотрим приёмы идеализации, которые порождают плоские расчётные схемы, создаваемые на базе упру-
гой линии.
Характерным для этого класса систем является то, что как в исходном, так и в деформированном состоянии их базовые элементы остаются в одной и той же плоскости. Необходимым условием этого является расположение векторов внешних воздействий в той же самой плоскости.
31

2.1. Идеализациявнешнихвоздействий
Характер
природных
воздействий
Сосредоточенные
нагрузки
Распределённые полиниинагрузки
Сосредоточенный момент сил
Способы внешних воздействий
Виды нагрузок
Расчёт по недеформированной схеме
Принцип
независимости
воздействий
В природе внешние воздействия являются распределёнными по поверхности или по объёму материального тела. С целью упрощения описания этих воздействий их
приводят к некоторым условными нагрузкам. Например, если нагрузка распределена по части по-
верхности и площадь этой части составляет малую часть всей поверхности, то такую нагрузку считают сосредото-
ченной в точке поверхности.
Если нагрузка распределена по площади, имеющей один размер значительно меньше другого, то такую на-
грузку принимают распределённой по линии поверхности. Понятие момента сил возникает, когда две незначи-
тельные по размеру площади нагружены распределённыминагрузками, равнодействующиекоторыхнаправленыв
противоположные стороны.
По способу воздействия нагрузки можно разделить на силовые, кинематические (нагрузки-перемещения) и температурные.
Нагрузки могут зависеть от времени. Если воздействие во времени меняется мало, то оно классифицируется как статическое. В противном случае воздействие явля-
ется динамическим.
Статические нагрузки могут быть дифференцированы, например, на временные и постоянные. Динамические нагрузки, в свою очередь, могут быть кратковременными (удар), периодическими (гармоническими), хаотическими (сейсмическими). Существуют и другие
признаки классификации нагрузок.
В классической строительной механике принято считать, что любое внешнее воздействие приложено к недеформированной расчётной схеме. Эта гипотеза основана на том, что поперечные перемещения упругих линий системы под нагрузкой считаются малыми настолько, что ими можно пренебречь в сравнении с габаритными размерами расчётной схемы при формировании условий рав-
новесия.
Считается также справедливым принцип независимости (наложения) действия нагрузок: результат действия нескольких нагрузок можно получить суммировани-
32

Нагрузки и глобальная система координат
Y 
 X
X
Z
Y 

 X
X 
 Z
Z
ем результатов действия каждой из нагрузок в отдельнос-
ти.
Для изображения приложенных красчётнойсхеме силовых и кинематических воздействий используются векторные обозначения. В связи с этим для таких нагрузок вводитсяправилознаком, связанноеспонятием«глобаль-
ная система координат» (ГСК).
Это прямоугольная прямолинейная система координат, оси X, Y которой располагаются в плоскости расчётной схемы, а ось Z направлена ортогонально этой плоскости. Обычно при этом ось X направлен по горизонтали вправо от начала координат, ось Y – вверх, а ось Z своим
положительным направлением «смотрит» на зрителя. Положительными считаются направления в сторону
положительных концов осей ГСК, а также углы поворотов, осуществляемые против часовой стрелки (если смотреть с конца положительной полуоси). Это правило далее будем именовать «математическим» правилом знаков.
2.2. Идеализацияэлементовконструкции
Внутренние
силовые
факторы
Простейшая классификация элементов строительных сооружений различает следующие их виды в соответствии с соотношением габаритных геометрических размеров:
•стержни – элементы, один размер которых значительно превышает два других, которые, в свою очередь, соизмеримы между собой;
•пластины и оболочки – элементы, один размер которых значительно меньше двух других, соизмеримых между собой;
•массивные тела – элементы, все размеры которых соизмеримы между собой.
Строительная механика стержневых конструкций имеет дело только со стержнями, которые в расчётной схеме изображаются отрезками упругих линий: прямых,
кусочно-ломаных или кривых.
Считается, что в любой точке упругой линии существует два сечения, в каждом из которых при искажении
33

Гипотеза
естественно
ненапряжённогосо
стояния
Метод сечений и внутренние силовые факторы
Виды усилий и локальная система координат
yx
 z
z
,n |
|
|
|
y |
|
|
|
|
|
|
, |
|
0x |
||
> |
|
|
|
N |
|
|
|
|
|
0 |
|
|
> |
|
|
z,b Q |
|
|
|
формы и/или размеров линии возникает система силовых факторов (усилий), которая уравновешивается такой же
системой факторов второго сечения.
Предполагается, что при отсутствии внешних воздействий искажение формы и размеров упругой линии не происходит, а в сечениях упругой линии внутренние си-
ловые факторы отсутствуют.
Если же такие воздействия присутствуют и упругая линии им сопротивляется, то в сечениях каждой точки этой линии возникают пары взаимно уравновешенных внутренних силовых факторов, которые «проявляются» с помощью метода сечений из условий равновесия любой из частей упругой линии, выделенных выполненным раз-
резом.
В общем случае нагружения эти факторы представлены продольной N и поперечной Q силами, а также изгибающим моментом M. В связи с тем, что упругая линия не обязательно является прямой, в расчётной схеме может использоваться «локальная» система координат x, y, z
(ЛСК).
Такая система «привязывается» к каждой точке упругой линии так, чтобы ось x была направлена вдоль этой линии в сторону возрастания её длины. Ось z ЛСК параллельна оси Z ГСК и направлена в ту же сторону. Ось y ортогональна плоскости (x, z) и образует с ней правую декартову систему координат: при взгляде с положительного направления оси z на плоскость (x, y) поворот оси x к оси y должен осуществляться против часовой стрелки (мате-
матическое правило знаков).
В случае, когда упругая линия представлена кривой, ось x совпадает с направлением касательной, а ось y – c направлением нормали в начале координат. Таким образомпродольнаясилаN вэтомслучаетакженаправленапо касательной, а поперечная сила Q – вдоль нормали.
34
Инженерное правилознаковдля усилий:
- знак N;
- знак Q;
- знак М
Положение
растянутых
волокон
Линейная
зависимость
усилий от деформаций
Поперечные силы зависят от изменения момента
Для внутренних силовых факторов в сечении упругой линии традиционно используется «инженерное» правило знаков, согласно которому направленное «от сечения» (растягивающее) продольное усилие N считается положительным.
Если поперечное сил Q вращает сечение, к которому она приложена, по часовой стрелке, то она также считается положительной.
Момент в сечении знака не имеет. В отношении него действует соглашение: при построении графика распределения момента по сечениям (эпюры момента) его ординаты (без знака!) откладываются с той стороны сечения,
которая подверглась растяжению.
Здесь необходимо вспомнить, что при изгибе, согласно гипотезам о плоских недеформируемых поперечных сечениях брусьев, ортогональных упругой линии до и после деформации, волокна сечения на выпуклой стороне бруса растягиваются, а на вогнутой – сжимаются. Поэтому положение этих волокон легко определить по форме
деформированной упругой линии.
Деформирование упругой линии приводит к возникновению внутренних силовых факторов, значения которых определяются возникающими малыми деформация ми. В сопротивлении материалов доказано, что при малых перемещениях имеется следующая линейная связь
между усилиями и деформациями: |
N = EF , |
|
M = EJ ; |
Q = GF ; |
|
где – соответственно деформация изгиба (кривизна), сдвига и осевая; – коэффициент неравномерности распределения касательных напряжений по поперечному сечению (1,2 для прямоугольной и 1,11 для круглой формы сечения).
Из этих соотношений следует, что усилия и деформа-
ции связаны линейными зависимостями.
С другой стороны, из уравнений равновесия при изгибе для малых поперечных перемещений следует, что изгибающий момент в сечении «порождает» поперечную
силу |
в |
этом |
же |
сечении |
по |
закону |
Q = |
dM dx |
= tan M . Эта зависимость позволяет оп- |
||||
ределять значения поперечных сил по тангенсам острых
35
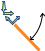
Определение знакаQпоэпюреM
Продольные силы зависятотнагрузки и поперечных сил
углов наклона касательных линий эпюры изгибающего
момента к осям расчётной схемы.
Поперечная сила является положительной, если поворот касательной на эпюре М до её совмещения с упругой линией производится по часовой стрелке.
Связь момента и N считается отсутствующей. Этот факт даёт возможность утверждать, что появление продольных сил N в сечениях может иметь причиной:
1)наличие нагрузки, параллельной оси упругой ли-
нии;
2)условия равновесия в точке упругой линии, когда еёсечениянепараллельны, т.е. когдаусловиясамоуравновешенности сил в сечениях точки требуют проектирования возникающей поперечной силы на направление искомой продольной силы.
S |
-S |
|
K |
|
|
|
|
Рассмотрим точку К расчётной схемы, в которой со- |
|
Q |
|
NK-S |
|
единены два сечения K-S и K-L упругих линий, имеющих |
|||||
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
разные направления. |
|
|
N |
Q |
-L |
|
||||
|
|
K |
|
||||||
|
|
|
K |
|
|
|
Удовлетворяя условиям равновесия внутренних сил, |
||
|
|
|
- |
|
|
|
|
||
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Lполучим их выражения в общем случае, который определяется углом между направлениями K-S и K-L:
«Превращение»поперечныхсилвпродольные
– QK – S + N K – L sin + QK – L cos = |
0, |
||
N K – S – N K – L cos + QK – L sin = |
0; |
||
N K – S |
= |
– QK – L + QK – S cos sin , |
|
N K – L |
= |
QK – S – QK – L cos sin . |
|
Нетрудно видеть, что при любом угле |
0 про- |
||
дольные силы зависят от поперечных.
В характерном для расчётных схем случае, когда линии K-S и K-L образуют угол 90о, значения продольных сил в каждом из сечения определяются только значения ми поперечной силы в другом сечении.
Такимобразом, врамкахиспользуемойсистемыгипотез, продольные силы в расчётной схеме определены нагрузкой вдоль упругой линии и значениями поперечных сил, возникающих вследствие изгиба смежных линий.
36

2.3. Идеализацияспособовсоединения элементоввконструкцию
Понятие диска расчётной схемы
Степени свободы диска на плоскости
Число
степеней
свободы
системы
несвязанныхдисков
Способы
запрета
степеней
свободы
Куда «исчезают» нагрузки на сооружение?
Земля какединыйопорный диск
Одним из необходимых условий возможности сопротивления упругой линии внешним воздействиям является отсутствие у неё перемещений в плоскости как жёсткого
целого, т.е. без изменения размеров и формы.
Отрезок упругой линии, рассматриваемый как жёсткое целое, принято называть диском. На плоскости диск имеет три независимые перемещения, именуемые степенями свободы:
•поступательные W x W y вдоль осей X, Y ГСК соответственно;
•вращательную W z относительно оси Z ГСК.
Чтобы определить эти перемещения диска, их измеряют на плоскости относительно неподвижного начала
ГСК.
Понятно, что в состав расчётной схемы сооружения входит не один диск, но каждый из них имеет относительно ГСК по три степени свободы. Общее число степеней свободы системы дисков принято обозначать как W. Таким образом, чтобы обеспечить неподвижность системы
из D дисков, следует запретить W = 3D перемещений. Запрет перемещений отдельного диска можнообеспе-
чить двумя способами:
1)соединением дисков между собой;
2)соединением дисков с опорой сооружения. Первый способ обеспечивает совместную работу эле-
ментов сооружения под внешними воздействиями и вы-
деление полезного объёма пространства.
Второй способ обеспечивает передачу внешних воздействий с сооружения на землю, поскольку опыт строительства показывает, что земля обладает абсолютным сопротивлением большинству природных воздействий. Правда, для гарантированной передачи этих воздействий требуется применение массивных тел, именуемых опо-
рам.
Поскольку опор у сооружения может быть много, а поверхность земли, на которой они располагаются, одна,
37

то в строительной механике принято говорить о единственном опорном диске – земле. Опоры же рассматриваются как способ передачи нагрузки с сооружения на землю.
S |
|
|
|
|
|
Основнаяидеязапретапоступательногоперемещения в заданном направлении заключается в том, чтобы поставить на пути смещающейся точки диска непреодолимую
преграду.
В качестве такой преграды условились считать абсолютно жёсткий стержень одним концом присоединяю щийся к точке, которая не должна перемещаться поступательно, а вторым – к опорному диску или точке другого диска. При этом ось стержня параллельна направлению предполагаемого перемещения. Из теоретической механики известно, что подобный стержень способен воспринимать осевую силу на одном конце и без изменения её
Sзначения и направления передавать вдоль оси на другой
Понятие связи 1-го вида
Wy

 W z
W z


 W z
W z 



 Wy
Wy
конец.
Таким образом в строительную механику вводится понятие «связь 1-го вида»: это условное, не имеющее размеров, абсолютно твёрдое тело, которое реализует передачу сосредоточенной силы между двумя точками. Эти точки являются центрами плоских шарниров, на которые,
как принято считать, опирается тело связи.
Связь 1-го вида препятствует сближение/удалению центров шарниров вдоль оси связи, но не мешает относительному вращению точек приложения силы и не препятствует смещению центров шарниров вдоль направления, ортогонального оси связи.
При наличии нагрузки на систему дисков в связях 1- го вида возможно возникновение осевых сил. Эти силы, в зависимости от расположения связи, принято трактовать как реактивные (если связь стоит между сечением диска и опорным диском) или внутренние (если связь стоит между сечениями двух дисков).
Общее число опорных связей в расчётной схеме обычно обозначают как Co .
Чтобы различать эти два случая по возникающим силам, условимся обозначать так:
38

Обозначения
реакций
опорных
связей
Обозначения усилий вовнутреннихсвязях
Две параллельныесвя- зи1-говидапереда- ют сосредоточенную силу и момент
XK K S
ZK  YK
YK
• одним индексом в случае опорной связи, например, X K – сила, возникающая в связи между сечением диска и
точкой на опоре, образующими опорный узел К; эта сила приложена к сечению К диска и направлена горизонталь-
но, так как связь 1-го вида имеет горизонтальную ось;
• двумя индексами в случае связи между сечениями дисков, например, N K – S – сила, возникшая в связи меж-
ду сечениями точки К, образующими внутренний узел расчётной схемы; эта сила приложена к сечению, принадлежащего участку диска K-S; при этом ось связи парал-
лельна оси участка K-S.
В одном опорном узле у диска можно отобрать все три степени свободы относительно земле. Для этого в опорном сечении диска достаточно установить три связи 1-го вида: пару связей, параллельных между собой (они обеспечатотбородногопоступательногоиугловогоперемещения), и ещё одну связь, ортогональную этой паре (она запрещает второе независимое поступательное пере-
мещение).
Напомним, что связи 1-го вида не имеют размеров и являются условным изображением способа передачи нагрузки на землю. Тем не менее, пара сил, возникающих в параллельных связях, в соответствии с правилами приведения сил на плоскости, образуют сосредоточенную силу
и момент.
Соответствующие реактивные силы и момент в опорном узле имеют обозначения: X K Y K Z K . Эти обозначения соответствуют составляющим реактивной силы и мо мента на оси ГСК в опорном сечении К диска конструк ции.
Для этих составляющих применяется математичес-
кое правило знаков.
Аналогичным образом можно устранить относительные степени свободу между парой сечений двух дисков (диски расположены на одной, так как связи размеров не имеют!).
39
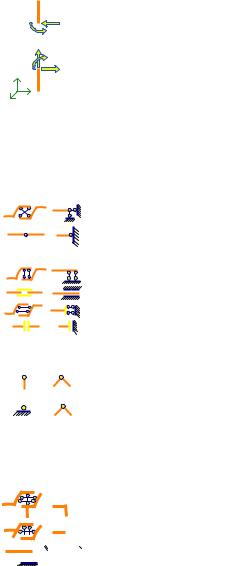
K LQK-L
MK-L NK-L
NK-L
MK-S NK-S K QK-S
S
Связи 2-го и 3-го видов
(1) |
|
|
(1) |
|
|
|
|||
K |
K |
|||
|
|
|
|
|
В этом случае составляющие внутренних сил обозначатся по правилу, приведенному выше:
• в сечении K-S это X K – S Y K – S Z K – S ;
• в сечении K-L это X K – L Y K – L Z K – L .
Для этих усилий применяется инженерное правило знаков.
Вполне естественно, что и в опорных узлах и во внутренних узлах дисков можно использовать не все связи. Чтобы упростить графические изображения соответствующих узлов, вводят понятия связей 2-го и 3-го видов.
Будем говорить о дефекте узла по связям, если через
его связи передается только одна или две силы.
При передаче пары сосредоточенных сил говорят о связи 2-го вида типа «шарнир» (иногда такие связи называют шарнирной заделкой). В таком узле между сечения-
ми возможно относительный поворот.
Если передаются сосредоточенная сила и момент, то говорят о связи 2-го вида типа «ползун». В этом случае по направлению, ортогональному направлению передаваемой силы, между сечениями узла возможно относитель-
ное поступательное перемещение.
В K-узле расчётной схемы могут соединяться S 2 сечений дисков. Если между некоторыми парами сечений установлены связи 2-го вида, узел характеризуют «крат-


 ностью шарнира» ШK 1 = S – 1 . Отдельная связь 2-го
ностью шарнира» ШK 1 = S – 1 . Отдельная связь 2-го
вида обладает кратностью 1. Суммарная кратность всех связей 2-го вида в расчётной схеме вычисляется как
Ш 1 = ШK1 .
K
Связи 3-го вида называют жёсткой заделкой, так как
через сечения соответствующего узла передаются все
усилия, которые могут возникать в модели стержня типа



 «упругая линия»: две сосредоточенные силы и момент.
«упругая линия»: две сосредоточенные силы и момент. 
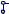


 Таким образом, можно считать, что все внутренние узлы одного диска образованы связями 3-го вида.
Таким образом, можно считать, что все внутренние узлы одного диска образованы связями 3-го вида.
40

Усилия
иреакции
всвязях 1-го вида
Поскольку связи обеспечивают передачу сил между сечениями, важно правильно интерпретировать условные обозначения связей. Ниже приведены характерные случаи обозначений соединения сечений дисков между собой и с землёй, а также силы, передаваемые соответствующими связями.
1 |
2 |
|
|
1 2 |
2 3 |
1 |
2 |
Q2-1 |
|
|
|
|
|
|
|
||
Q2-1 2 3 |
|
N2-1 |
2 |
3 |
2 |
1 2 N2-3 |
||
|
2 3 |
|
3 |
2 |
||||
1 2 Q2-3 |
1 2 |
N2-3 |
|
3 |
||||
|
|
|||||||
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
|
|
|
Y2 |
|
|
||||
|
|
|
|
|
|
|
X2 |
|
Заметим, что все силы указаны как положительные с использованием математического (для реакций) и инженерного (для усилий) правила знаков.
|
1 |
2 |
3 |
|
1 |
|
|
2 |
3 |
1 |
2 |
3 |
Q2-1 |
|
|
|
|
N2-1 |
N2-3 |
Q2-1 |
|
Q2-3 |
|||
1 2 2-1 |
2 3 |
|
1 2 |
|
2 3 |
|||||||
|
|
|
|
|
|
|||||||
Усилия |
|
N2-1 |
Q2-3 |
1 |
2 |
|
|
2 |
3 M2-1 |
|
M2-3 |
|
и реакции |
|
|
|
|
|
M2-1 |
|
M2-3 |
|
|
|
|
в связях |
1 |
2 |
|
|
|
1 |
|
2 |
|
|
|
|
2-го вида |
|
|
|
|
|
1 |
2 |
|
||||
|
|
|
|
|
|
|
|
|||||
|
Y2 |
|
|
|
|
Z2 |
|
|
Y2 |
|
||
1 |
2 |
|
|
|
1 |
2 |
|
1 |
|
|||
X2 |
|
|
X2 |
|
Z2 |
|
||||||
Усилия |
|
|
|
|
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
и реакции |
|
|
|
|
|
|
|
|
|
|
|
|
в связях |
|
|
1 |
2 |
3 |
|
|
|
1 |
2 |
|
|
3-го вида |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
M2-1 |
M2-3 |
|
|
Y2 |
|
|
|
||
|
|
2-1 |
3 |
|
1 2 |
X2 |
|
|
||||
|
|
1 2 |
|
|
2 |
|
|
|
|
|||
|
|
N2-1 N2-3 Q2-3 |
|
Z2 |
|
|
|
|||||
41
Г Л А В А
3
КИНЕМАТИЧЕСКИЙ АНАЛИЗ РАСЧЁТНЫХ СХЕМ
Назначение
сооружения
Деформации
элементов сооружения – причина сопротивления внешним воздействиям
Ни расчётная схема в целом, ни любая её часть не должныиметьстепеней свободы
Выше мы акцентировали вниманием на том, что любое сооружение призвано решить две основные задачи:
1)оградить от окружающей среды часть пространства для создания в нём условия, в которых нуждается человек;
2)использовать конструктивные элементы таким образом, чтобы они сопротивлялись внешним воздействиям.
Одной из главных задач строительной механике и является выявление условий, при которых возможно реше-
ние второй задачи.
Накопленный опыт показывает, что внешние воздействия посредством сооружения передаются на землю. При этом неизбежно возникают перемещения и деформации конструктивных элементов сооружения. Но только при наличии деформаций во всех элементах сооружения возможно возникновение внутренних сил как сил противо-
действия нагрузке.
Известны случаи, когда возведённое сооружение не смогло выполнить свои задачи, потерпев аварию или даже разрушившись, по причине возникщих в системе перемещений при реализации степеней свободы отдельных элементов конструкции. Такие элементы не могут сопротивляться внешним воздействиям запланированным образом.
Общее число степеней свободы системы дисков на плоскости равно утроенному их числу. Казалось бы, что еслив систему дисковввести столькожесвязей1-го рода, то проблема будет решена!
42
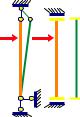
Связи могут быть наложены неправильно:
Две стороны кинематического анализа
К сожалению, всё оказывается не так просто. Дело в том, что минимально необходимое число связей решают проблему только при условии, что они расставлены строго определённым образом – «правильно». Более того, даже избыточное число связей может быть расставлено неверно!
Ещё раз отметим, что при неверно установленных связях, возможны перемещения элементов расчётной схемыбезихдеформирования. Величинатакихперемещений роли не играет – внутренние силы при отсутствии деформаций не возникают.
Таким образом, для обеспечения сопротивления сооружения внешним воздействиям требуется не только оп-
ределить количество связей для соединение элементов конструкции между собой и с землёй, но и правильно расставить эти связи.
Поставленные задачи решаются в разделе строительной механики, который называется кинематическим ана-
лизом.
Кинематический анализ, в соответствии с поставленными вопросами, имеет две стороны:
1)количественная сторона кинематического анализа устанавливает соотношение между степенями свободы, имеющимися у дисков расчётной схемы сооружения, и установленным числом связей 1-го вида;
2)качественная сторона кинематического анализа устанавливает критерии правильности расстановки этого количества связей.
3.1. Количественнаясторонакинематического анализа
Базовая |
Для расчётной схемы из D дисков, Ш 1 внутренних |
|
формула |
связей 2-го вида и Co опорных связей 1-го вида, число |
|
числа |
степеней свободы W можно определить так: |
|
степеней |
W = 3D – 2Ш 1 – Co . |
(3.1) |
свободы |
||
Слагаемые со знаком минус определяют способ «отбора» степеней свободы у дисков через соединение меж-
43

Случай
замкнутого
бесшарнирного
контура
Число степеней свободы плоскойшарнирной фермы
ду собой с помощью связей 2-го вида (шарниры, ползуны) и опорных связей 1-го вида общим числом Co . Понятно, что опорные связи 1-го вида могут образовывать и связи 2-го, и связи 3-го видов.
Применениеэтойформулыможетстолкнутьсяснекоторыми затруднениями, если, например, два диска систе-
мы соединены связью 1-го рода.
В этом случае стержень связи следует отнести к дискамрасчётнойсхемы(т.е. включитьеговчислоD), ашарниры, которыми он опирается на сечения дисков, вклю-
чить в число Ш 1 , увеличив его на 2.
Заметим, кстати, что любой диск расчётной схемы в форме ломаного бруса, опирающийся на два шарнира, может с точки зрения кинематического анализа считаться связью 1-го вида, так как векторы его реакции связей в сеченияхподсоединениялежатнаоднойпрямойипроходят
через центры опорных шарниров.
Другим случаем, когда применение формулы для числа степеней свободы W может привести к неверным результатам, является наличие в расчётной схеме диска, образующего замкнутый контур. Причём любая пара сече- нийэтогоконтураобъединяетсятремясвязями1-говида.
Иногда такой контур называют бесшарнирным.
Чтобы превратить такой контур в привычный диск в форме ломаного бруса, нужно сделать в одном из его узлов разрез, т.е. удалить три связи 1-го вида. Таким образом, формулу для подсчёта числа степеней свободы в случае наличия замкнутого бесшарнирного контура можно привести к виду
W = 3D – 2Ш 1 – Co – 3K . |
(3.2) |
Здесь К - число контуров с упомянутыми свойствами,
каждый из который включён в число D.
Первый вариант формулы для W можно применять и красчётнымсхемамтипа«ферма». Однакоболееудобной является формула:
W = 2У – S – Co |
. |
(3.3) |
Т.е., каждый узел У шарнирной фермы имеет две поступательные степени свободы, а каждый диск S фермы
44

можнорассматриватькаксвязь1-говида, котораяотбирает у узла одну степень свободы. Такую же роль играют и опорные связи 1-го вида.
3.2. Качественнаясторонакинематическогоанализа
Системауравнений для определения реакцийсвязейявляется неоднородной и линейной
Геометрическиизменяемые расчётные схемы
Статически
определимые расчётные схемы
Мгновенная
изменяемость
Понятие о «правильной» расстановке связей между дисками, включая опорный, определяется возможностью составления системы неоднородных линейных алгебраических уравнений (СЛАУ) для однозначного определения
реакций этих связей.
Неоднородность системы уравнений следует из того, что при определении реакций обязательным является использование уравнений равновесия, при составлении которых векторы внешних сил проектируются на оси системы координат и создают моменты относительно точек приведения независимо от реакций. Т.е., образуют, таким образом, свободные члены соответствующих уравнений.
Линейность же системы определяется тем, что неизвестные реакции в уравнения входят как неизвестные в первой степени.
Если для построения подобной системы уравнений ориентироваться на возможность составления для каждого диска плоской расчётной схемы трёх уравнений рав-
новесия, то возможны следующие ситуации:
1) число неизвестных реакций меньше числа уравнений равновесия – геометрически изменяемые системы; однозначное решение такой системы принципиально не
возможно; 2) число неизвестных реакций равно числу уравнений
равновесия – статически определимые системы; однозначность решения СЛАУ в этом случае зависит от значе-
ния определителя системы:
• определитель системы равен нулю – мгновенно изменяемые расчётные схемы; однозначного решения такой системы в общем случае нет;
45
Статически
неопределимые расчётные схемы
Понятие о заменяющей расчётной схеме
Условия
эквивалентности
заданной и заменяющей расчётных схем
Мгновенная
неизменяемость должна быть гарантирована
• определитель системы не равен нулю – мгновенно неизменяемые расчётные схемы, имеющие однозначное
решение.
3) число неизвестных реакций больше числа уравнения равновесия – статически неопределимые расчётные схемы; однозначное решение таких СЛАУ невозможно.
Таким образом, мы обнаружили две проблемы:
1)как избежать мгновенной изменяемости в статически определимых системах?
2)что делать, если уравнений равновесия не хватает для определения реакций в связях, наложенных на
расчётную схему?
В случае, когда уравнений равновесия не хватает, в строительноймеханикеиспользуютподход, сутькоторого заключается в замене исходной расчётной схемы на некоторую новую – заменяющую. Смысл такой замены в том, что:
•для заменяющей системы возможно составить достаточное количество уравнений равновесия;
•из некоторого условия эквивалентности обеих расчётных схем составляется недостающее количество
уравнений для заданной расчётной схемы.
Например, в методе сил заменяющая расчётная схема создаётсязаменой избыточного числа наложенных связей их реакциями. Значения этих реакций являются дополнительными неизвестными в заменяющей системе, а условия эквивалентности формулируется в форме требования:
по направлениями заменённых связей в заменяющей сис-
теме должны отсутствовать перемещения от всех действующих на заданную систему нагрузок, включая допол-
нительные реакции-неизвестные.
Итак, проблему недостающих уравнений можно решить, однако при этом для заменяющей расчётной схемы остаётся проблема обеспечения мгновенной неизменяемости, поскольку дополненная СЛАУ должна иметь однозначное решение.
46

Не следует торопиться составлять уравнения и вычислить определитель
системы!
Мгновенную
неизменяемость нужно определять до составления СЛАУ
Расчётная схема из одного диска
3.2.1. Способы обеспечения мгновенной неизменяемости
Сматематическойточкизренияпроблемамгновенной неизменяемости может быть решена достаточно легко – нужно просто вычислить определитель разрешающей СЛАУ. Но для этого такую систему нужно составить! Но, если определитель окажется нулевым вследствии неудач ного выбора заменяющей системы или неверного модели рования статически определимой расчётной схемой за данного сооружения, то придётся подобную же систему уравнений составлять для нового варианта расчётной схе мы.
Поскольку число попыток может оказать большим, такой подход оказывается весьма трудоёмким при расчё тах «вручную».
Правда, именно этот подход используется в автоматизированныхсистемахрасчёта. Однакотамзасчётбыстродействия ЭВМ и отсутствия неоднозначности замещающейрасчётнойсхемыпроблематрудоёмкостиневозника-
ет.
Более эффективным приёмом было бы определение признаков, по которым до составления системы разрешающих уравнений можно было получить гарантии мгновенной неизменяемости исследуемой расчётной схемы.
Наиболее простым способом определения мгновенной неизменяемости без составления разрешающей СЛАУ является построение поэтажной схемы из шар- нирно-стержневых треугольников.
Идея составления поэтажной схемы основана на способе обеспечения мгновенной неизменяемости расчётной схемы из одного единственного диска.
Поскольку у такого диска на плоскости имеется три независимые степени свободы, то для обеспечения передаче на землю нагрузки произвольного вида следует «отобрать» всетристепенисвободыустановкойсоответс-
тветствующих трёх связей 1-го вида.
Установкусвязейбудемпроводитьтак, чтобыобеспечить определение каждой реакции независимо от других. Для этого:
47
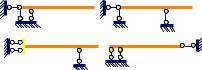
Доказательство
мгновенной
неизменяемости для расчётной схемы из одного диска
Варианты
образования
мгновенно
незименяемой расчётной схемы из одного диска
•одну связь установим горизонтально;
•вторую связь установим вертикально;
•третью связь установим так, чтобы она с первой или второй связью была параллельна (но не совпадала с ними), т.е. чтобы соответствующая пара реакций могла со-
здать реактивный момент.
Поскольку нагрузка произвольная, то каждая из реакций будет отлична от нуля, а это значит, что множитель при искомом значении реакции в соответствующем урав-
нении равновесия не может быть равным нулю.
Тогда, объединяя независимые уравнения равновесия в систему, мы при столбце неизвестных реакций получим диагональную матрицу размером 3х3. Определитель такой матрицы не равен нулю, так как равен произведению трёх отличных от нуля чисел, стоящих на главной диаго-
нали.
Итак, исходя из вышеизложенного, можно предложить следующие варианты образования мгновенно неизменяемой расчётной схемы из одного диска конструкции:
Свойства связей, обеспечивающих мгновенную неизменяемость объединения 2-х дисков
Рис. 3.1
Анализ расстановки связей в расчётных схемах на рис. 3.1. позволяет сделать следующие выводы:
•установленные связи 1-го вида непараллельны между собой;
•установленные связи не пересекаются в одной точ
ке;
•установленные связи образуют две несовпадающие точки пересечения своих направлений – мгновенные центры относительного вращения соответствующих связей.
Последнее свойство может иметь геометрическую интерпретацию: приняв мгновенный центр вращения за шарнир (фиктивный или фактический), мы получает систему из трёх дисков (конструктивный, опорный и диск связи 1-го вида) и трёх шарниров, которые не лежат на
48

Варианты
образования 3-х шарниров из трёх связей
1-говида,когдаони не параллельны и не пересекаются между собой
одной прямой и попарно соединяют упомянутые три дис-
ка.
.
Понятие о шарнирностержневом треугольнике
Другая
интерпретация
способа образования ШСТ
Рис. 3.2
Такая схема получила наименование «шарнирностержневой треугольник» (ШСТ). А поскольку соответствующая расчётная схема образована с использованием одного конструктивного диска, который присоединён прямо к земле, то такую схему можно условно назвать
«первым этажом» сооружения.
Другой вариант образования первого этажа в виде ШСТ можно получить, если, как мы это делали выше, посчитать связью 1-го вида конструктивный диск, включённый в расчётную схему концевыми шарнирами. Но тогда нужно говорить о трёх дисках, попарно объединённых тремя шарнирами, не лежащими на одной прямой.
Заметим, что теперь расчётная схема представлена двумя конструктивными дисками и одним опорным дис ком, которые объединены тремя узлами, каждый из которых имеет дефект одной связи. Примеры объединения и соответствующие ШСТ приведены на рисунке.
Варианты |
|
|
|
||
образования |
|
|
|
||
|
|
|
|
||
мгновенно |
|
|
|
|
|
незименяемой |
|
|
|
|
|
расчётной схемы |
|
|
|
|
|
из двух дисков |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
|
|
Рис. 3.3
!


49

Каждый ползун расчётной схемы из двух дисков и земли порождает фиктивныйшарнир в ШСТ
Два диска и земля объединены двумя ползунам и шарниром
Признаки
мгновенной неизмяемости, основанные наструктуресвязей в узлах объединения 2-х дисков между собой и с землёй
Обратите внимание! Наличие связей 1-го вида, объединённых в ползуне (опорном и/или внутреннем), при построении ШСТ требует образования фиктивного шарнира. При этом каждый ползун порождает один фиктив-
ный шарнир.
Наличие ползунов в 2-х узлах позволяет построить ШСТ по той же схеме, что и ранее. Т.е. каждая связь 1-го вида одного ползуна, пересекаясь с одной из связей второгоползуна, образуетфиктивныйшарнир. Этапарашарниров и безмоментный шарнир анализируются на соответствиеневырожденномутреугольнику, т.е. тришарнира не должны лежать на одной прямой.
Заметим, что наличие двух фиктивных шарниров приводит к тому, что между ними образуется фиктивная же связь (фиктивный диск).
|
|
|
|
" |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
" |
|||
|
|||
|
|
||
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.4 |
|
||
Досихпормыисходилиизтого, чтосвязимеждудисками в расчётной схеме из 2-х дисков и земли позволяли построить ШСТ из действительных или фиктивных без моментных шарниров. Можно, однако, использовать и другой приём, основанный на анализе структуры шести
связей, образующих эти шарниры.
В самом деле, возможность образования ШСТ в указанной расчётной схеме существенно основана на том, что существует три точки попарного пересечения связей, образующих реальные и/или фиктивные шарниры. А это значит, что соответствующие шесть связей:
1)не пересекаются в одной точке;
2)не параллельны между собой;
3)имеют не более 3-х параллельных связей.
50
Поэтажнаясхема– какпоследовательность шарнирностержнвых невырожденных треугольников
Каждый предыдущий этаж можно рассматривать как первый дляпоследующего
Таким образжом, элементарная плоская расчётная схема может образована одним из следующих способов:
•присоединением к земле одного диска конструкции;
•присоединением к земле пары дисков, соединённых между собой шарниром или ползуном.
Условия «правильности» объединения дисков основа ны на понятии невырожденного шарнирно-стержневого
треугольника.
Расчётные схемы даже сравнительно простых сооружений конечно же состоят из более, чем 2-х дисков конструкции. Однако анализ их мгновенной неизменяемости также может быть построен на базе понятия ШСТ.
Для этого вводится понятие «поэтажная схема». Смысл этого понятия простой: этажом является любой шарнирно-стержневой треугольник, образованный либо только из дисков конструкции, либо из дисков конструк-
ции и опорного диска.
Спримерамиобразования1-гоэтажамыужепознако- мились. Для образования 2-го этажа достаточно 1-й этаж считать опорным диском, поскольку он способен выполнять такую роль, передавая нагрузки на землю. А далее вновь пытаться образовать «первый этаж», в котором роль опорного диска выполняет этаж, ранее образованный. Понятно, что вновь образованный этаж удобнее называть вторым этажом.
Указанный процесс следует повторять до тех пор, пока не будут задействованы все диски расчётной схемы. Пример образвания поэтажной схемы для многопролёт-
ной рамы приведен на рисунке.
.
Каждомуэтажусоответствует свой шарнирно-стержне- вой треугольник
1 |
4 |
2 3
1
1234 ! " # !$
Рис. 3.5
Обратите внимание! Следует понимать, что опорный диск «земля» является единственным представите-
51
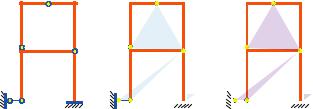
Шарнирностержневой треугольник из трёх дисков конструкции
Понятие
офиктивномэтаже расчётной схемы
лем опорных дисков. Поэтому включение его в ШСТ может быть произведено только единожды! Но этот факт не противоречит тому, что опорных узлов на этом диске может быть сколь угодно много. Т.е. в многоэтажных расчётных схемах диски 2-го и последующих этажей могут иметь опорные узлы как на земле, так в узлах дисков
предыдущих этажей.
Рассмотрим, наконец, вариантобразованияШСТ, когда два соединённых между собой диска узлом типа шарнир или ползун, опираются не на землю, а на третий диск, который также является диском конструкции.
Понятно, что даже невырожденный ШСТ такого вида не может играть роль первого этажа, так как, не имея связей с землёй, он не может воспринимать внешние воздействия, оставаясь в равновесии, – напомним, что все виды внешних воздействий на сооружения передаются на
землю!
Но! Такой ШСТ является мгновенно неизменяемым, и, следовательно, может рассматривать в качестве отдельного диска, а точнее «супердиска», конструкции. При такой интерпретации ШСТ из трёх конструктивных дисков появляется возможность образования фиктивных «этажей» расчётной схемы.
Этот приём оказывается полезным, так как позволяет начинать построение поэтажной схемы не только с использования опорного диска, но и с любого невыроженного ШСТ.
Варианты
образования поэтажной схемы двузэтажнойрамы
3 |
|
|
|
1 |
|
|
|
2 |
|
|
|
2 |
|
|
|
1 |
|
3 |
|||||
|
|
||||||
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.6
52

Что касается признаков мгновенной неизменямости, тоониничемнеотличаютсяотслучая, когдатретьимдиском выступает опорный диск (земля).
Построение поэтажной схемы возможноневсегда!
При отсутствии нагрузкивсеусилия должны определяться однозначено как нулевые
В основе метода нулевой нагрузки лежит свойство определителя системыуравнений равновесия
3.2.2. Способы определения мгновенной неизменяемости
В тех случаях, когда не удаётся построить поэтажную схему для заданной расчётной схемы, могут использоваться приёмы, которые совмещают анализ мгновенной изменяемости со статическим расчётом. Эти приёмы базируются на свойствах определителя составляемой систе мы уравнений.
Рассмотрим, в частности, два приёма:
•способ нулевой нагрузки;
•способ замены связей.
Способ нулевой нагрузки основан не том, что со-
гласно гипотезы начального ненапряжённого состояния, при отсутствии нагрузки все усилия в заданной расчётной схеме должны быть равны нулю. В мгновенно неизменяемой системе это означает, что определение этих усилий по уравнениям равновесия даёт однозначные и при том нулевые значения усилий.
Если в процессе определения этих усилий мы встречаем процедуру вычисления типа деления на нуль (что даётнеопределённыйрезультат), тоэтотфактсвидетельс-
твует о мгновенной изменяемости системы.
Такойвыводможетбытьобосновантем, чтовслулчае присутствия нагрузки столбец свободных членов системы уравнений равновесия имеет элементы с ненулевыми значениями. Т.е. система уравнений является неоднородной. Решение такой системы будет однозначным только при условии ненулевого значения определителя этой системы. Следовательно, и в случае нулевых значений элементов столбца (нагрузка отсуствует) определитель системы должен оставаться ненулевым.
Такчтоприменениеэтогоспособаможнореализовать
вдвух формах:
1)вычислением определителя системы уравнений равновесия заданной расчётной схемы;
53
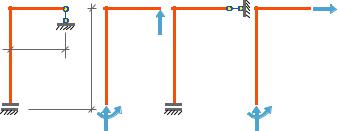
Пример
применения
способа нулевой нагрузки
2) последовательным определением неизвестных системы равновесия с анализом их значений на однознач-
ность.
Рассмотрим применение способа нулевой нагрузки на элементарном примере.
2 |
3 |
Y3 |
|
X3 |
|
a |
|
||
|
|
|
|
|
|
2a |
|
|
|
1 |
|
Z1 |
|
Z1 |
|
a |
Y1 |
# |
Y1 |
При составлении определителя использован столбец неизвестных, расположенных именно порядке
Z1, Y1, Y3
Рис. 3.7
Составим уравнения равновесия для определения реакций Z1 Y 1 Y 2 для расчётной схемы рис. 3.7, а.
Z1 mom1 |
= 0 |
= |
Z1 + Y 3 a; |
||||
Y 1 mom3 |
= 0 |
= |
Z1 – Y 1 a; |
||||
Y 3 Y = 0 = Y 1 + Y 3; |
|||||||
|
|
|
|
|
|
|
|
det |
1 |
0 |
a |
= – a + a = 0. |
|||
1 |
–a 0 |
||||||
|
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Вычисление определителя даёт его нулевое значение, что соответствует мгновенной изменяемости расчётной схемы, приведенной на рис. 3.7, а. Мгновенная изменяемость этой схемы очевидна: один диск опёрт на три параллельные (вертикальные) связи 1-го вида, что обеспечиваетмгновеннопоступательноеперемещениеломаного бруса по горизонтали.
Перейдём ко второй расчётной схеме рис. 3.7, б.
54
Используем те же самые уравнения равновесия для
При составлении |
определения неизвестных реакций Z1 Y 1 X 3: |
||||||||
|
|
|
|
|
|
|
|
||
определителя |
Z1 mom1 = 0 |
= |
Z1 + X 3 2a; |
||||||
столбец |
|||||||||
использован |
Y 1 mom3 |
|
|
|
= Z1 – Y 1 a; |
||||
неизвестных, |
= |
0 |
|||||||
|
|
|
|
|
|
|
|
||
расположенных |
Y 2 |
|
Y = 0 = Y 1; |
||||||
именно порядке |
|||||||||
|
|
|
|
|
|
|
|
||
Z1, Y1, X3 |
|
|
|
|
|
|
|
|
|
|
det |
|
1 |
0 |
2a |
= 2a 0. |
|||
|
|
1 –a |
0 |
|
|||||
|
|
|
0 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Мгновенную
неизменяемость
заменяющей системы следует доказывать с помощью шарнирностержневых треугольников
Уравненияспособа замены связей формируются на базе принципа наложения
Таким образом, расчётная схема рис. 3.7, б мгновенно неизменяемая, что также вполне очевидно: один диск соединён с землей тремя связями 1-го вида, которые не параллельны между собой и не пересекаются в одной точке.
Способ замены связей основан на использовании заменяющей расчётной схемы. Смысл создания заменяющей системы в том, чтобы её мгновенная неизменямость
была легко доказуема.
Как следует из наименования способа, замещающая система получается преобразованием заданной с помощью замены связей. Количество таких связей зависит от простоты доказательства мгновенной неизменяемости за мещающей системы. Рекомендуется обходиться минимальным количеством заменяемых связей.
Замена каждой связи в системе должно сопровождаться введением в замещающую систему дополнительной нагрузки в виде реакций в сечениях, выделяющих такую связь.
Напомним, что в кинематическом анализе в качестве связи 1-го вида может выступать любой шарнирно опёртый по концам диск. В том числе могут быть использова-
ны фиктивные шарниры и/или фиктивный диск. Условием эквивалентности заданной и заменяющей
систем является требование: во вновь поставленных связях от совместного действия заданной и дополнительной нагрузок не должны возникать реакции, если заданная
55
Определение
реакции взаменённойсвязи должно быть однозначным для мгновенно неизменямой системы
Метод замены связей позволяет начать расчёт мгновенно неизменяемой системы
расчётная схема является мгновенно неизменяемой. Что вполне понятно – реальные связи на новых местах не су-
ществуют, значит, отсутствуют и реакции в них.
Если при описанных условиях применения способа замены связей удаётся однозначно решить соответствующую систему уравнений, то заданная расчётная схема является мгновенно неизменяемой.
И в этом случае доказательство мгновенной неизме няемости опирается на ненулевой значение определителя сформированной системы уравнений эквивалентности заданной и заменяющей систем.
А поскольку речь идёт о вычислении реакций во вновь расставленных связях, то мы их определяем из уравнений равновесия. Т.е. определитель формируется на базе уравнений равновесия заменяющей системы и её
частей.
Обратите внимание! Неизвестными в уравнениях эквивалентности являются реакции заменяемых связей. Такимобразом, мынетолькоможетдоказатьмгновенную неизменяемость заданной расчётной схемы, но и частично получить решение задачи об определении внутренних и/или внешних реакций.
Рассмотрим пример использования способа замены связей для элементарной расчётной схемы.
2 |
3 |
4 qa |
|
a |
2a |
|
|
|
1 |
|
5 |
|
a |
|
2 |
3 |
4 qa |
2 |
3 |
4 qa |
|
|
|
|
a |
2a |
|
|
|
|
|
|
1 |
|
5 |
1 |
|
5 |
|
# |
X5 |
|
|
|
|
|
|
|
Рис. 3.8
Заменяющая система примеров выбрана в виде ломаного бруса
Заменяющая система представлена расчётной схемой рис. 3.8, б. Для задачи рис. 3.8, а добавлена связь по продольной силе в узел 3. Для задачи 3.8, в добавлена связь по поперечной числе в тот же узел. В обеих задачах удалена горизонтальная связь в узле 5.
56

Принцип
наложения
используется двужды:
суммируются
воздействия
нагрузок и нагрузка от неизваестной реакции представлена
произведением её единичного значения на полное
Убедитесь, что способ заменысвязейдаёт правильное значение реакции
Таким образом, уравнения эквивалентности в предсталенных задачих должны описывать нулевые значения продольной и поперечной сил. Для этого воспользуемся принципом наложения воздействий:
|
N 3 – 4 = N 3 – 2= N qa + N X 5 = |
|||||||||
= |
N qa + |
|
|
|
|
|
5= 1 X 5 = 0 |
рис. 3.8, а, б |
||
N |
X |
|||||||||
|
Q3 – 4 = Q3 – 2= Q qa + Q X 5 = |
|||||||||
= |
Q qa + |
|
|
|
5= 1 X 5 = 0 |
рис. 3.8, в, б |
||||
Q |
X |
|||||||||
Решение задачи по определению продольного усилия в сечениях узла 3 представлено соотношениями:
N 3 – 4 qa X 3 – 4 – 5= – N 3 – 4 + qa= 0 N 3 – 4 X 5= 1 X 3 – 4 – 5= – N 3 – 4 + 1= 0
|
|
N qa |
|
N 3 – 4 |
qa |
|
|
X 5 |
= – |
-------------- |
= – |
------- |
= –-- |
= –qa |
|
|
N X 5= 1 |
|
N 3 – 4 |
1 |
|
||
Поскольку продольное усилие определено однозначно, заданная расчётная схема мгновенно неизменяемая. Правильность определения усилия легко проверить, составив условие отсутствия продольного усилия в ползуне узла 3: сумма проекций сил правой части ломаного бруса на ось Х даёт значение –qa.
Решение задачи рис. 3.8, в (определение Q3-4 = Q3-2):
|
|
|
|
|
|
|
|
qa |
= 0 |
Q3 – 4 qa Y 3 – 4 – 5= Q3 – 4 + -- |
|||||||||
|
|
|
|
|
|
2 |
|
||
Q3 – 4 |
|
5= 1 Y 3 – 4 – 5= – |
|
3 – 4 + 0= 0 |
|||||
X |
Q |
||||||||
|
|
|
Q qa |
Q3 – 4 |
|
qa 2 |
|
||
X 5 = – |
-------------- |
= – |
------ |
= –------ |
= |
||||
|
|
Q X 5= 1 |
Q3 – 4 |
0 |
|
||||
57
Неопределённость значения может бытьидругоготипа, например, 0/0
Неопределённое значение реакции в заменяемой свя зи свидетельствует о мгновенной изменяемости расчётной схемы на рис. 3.8, в. Это вполне понятно, так как два диска системы объединены тремя параллелльными связями: две горизонтальные в узле 3 и одна – между шарнирами 1 и 5 (её образует опорный диск – земля).
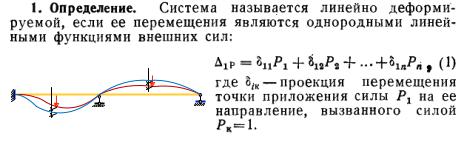
Г Л А4В А
Основные теоремы о линейно-деформируемых расчётных схемах
∆j j Pj
Pi
∆i j

8
