4.4. РАСЧЕТ ФЕРМЫ С ТРЕУГОЛЬНОЙ РЕШЕТКОЙ (АНАЛИТИЧЕСКИЙ СПОСОБ)

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тульский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Полезная литература.pdf

Скачиваний:

Добавлен:

16.03.2016

Размер:

8.65 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 2610 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

20,5 − 20,0 ; =

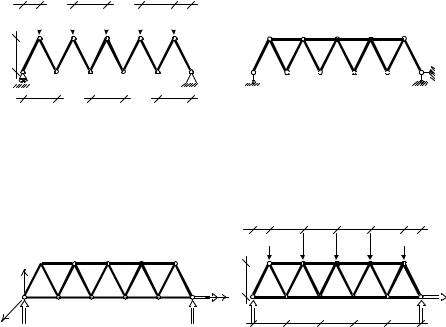
Особенностью расчетной схемы типа ферма (рис. 4.41) является наличие в сечениях ее стержней только Фродольных усилий, что обеспе- чивается как способом приложения нагрузки (сосредоточенные силы в узлах-шарнирах), так и способом соединения стержней фермы в узлах расчетной схемы – безмоментными шарнирами (рис.4.42).

0,5a a

a 0,5a

0,5P

Ðèñ. 4.41

Ðèñ. 4.42

На рис. 4.43 вводится система координат, оси которой определяют правило знаков для реактивных сил, заданных своими обозна- чениями. Реакции до их определения считаются Фоложительно направленными, как это проиллюстрировано на рис. 4.44.

X,Y,Z - глобальная система координатпривязанная, " к "

расчетной схеме

XB X

YA YB

Ðèñ. 4.43

0,5a a	a	a	a	0,5a
0,5P	P	P	P		0,5P
0,5P					0,5P
a					XB
					XB
YA					YB
a	a	a	a	a	YB
a	a	a	a	a

Ðèñ. 4.44

Ïî	данным рис. 4.44 назначаются уравнения равновесия (4.13)
для определения реакций опорных связей:
YA	∑momB = 0;	(1)	(4.13)
YB	∑Y = 0;	(2)	(4.13)
YB	∑Y = 0;	(2)
XB	∑X = 0.	(3)

Для определения реакции YA составим и решим первое уравнение последовательности (4.13):

114

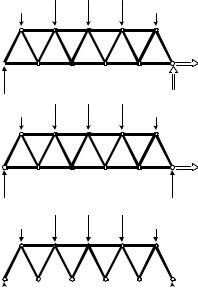
∑mom B = −YA 5a +

5a −

aJ + P G5a −

− aJ +

+ P F

5a − 1 a −

2aI

P F

5a −

1 a − 3aI

1 P F

5a −

1 a − 4aI

2 H

4 b

= −Y

5a +

14 +10 +

6 +1

= 0 Y

= 2P .

Наличие значения и направления реакции YA позволяет трансформировать рис. 4.44 в рис. 4.45, à.

0,5P	P	P	P	0,5P
0,5P				0,5P
				XB
2P		à		YB
2P		à
0,5P	P	P	P	0,5P
0,5P				0,5P
				XB
2P		á		2P
		á
0,5P	P	P	P	0,5P
0,5P				0,5P

В соответствии со вторым уравнением последовательности (4.13), привлекая данные рис. 4.45, à, записываем:

∑Y = 2P − 12 P − P −P − P

− 12 P +YB = 0 YB = 2P.

Заменив на рис. 4.45, à обозначение реакции YB найденным вектором, получаем рис. 4.45, á, по которому составляем третье уравнение последовательности (4.13) – для определения XÂ:

∑X = XB = 0 XB = 0.

Таким образом, реакции опор-

ных связей определены. Это позво-

ляет указать на расчетной схеме

все нагрузки в явном виде («в

Ðèñ. 4.45

значениях»), как это сделано на

ðèñ. 4.45, â. Данные

этого рисун-

êà

используются

äëÿ

проведения контроля правильности определе-

íèÿ

реакций опорных

связей по

уравнению:

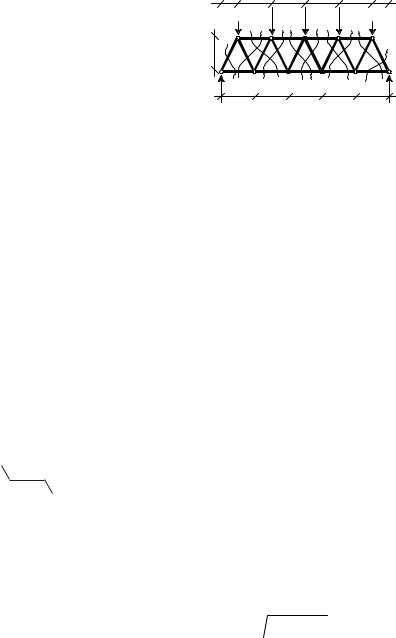
∑mom C = −2P 2a +

P Ga +

aJ +

− P Ga −

aJ −

− P Fa + 1 aI

− 1 P F2a +

1 aI

2P 3a =

(4.14)

2 K

−

1 Pa

+ 2 + 6 +

+ 1 Pa

+ 2 + 24

≡ 0.

115

Далее, в соответствии с операционным алгоритмом, требуется указать виды сечений, порядок их следования (рис. 4.46), а также уравнения, которые нужно составить для определения усилий в стержнях, попавших в соответствующие сечения последовательности:

0,5a	a	a	a	a	0,5a
0,5P		P	P	P	0,5P
2 C B4 D E6			F G8 H J10
A					K
a
1	3	5	7	9	11
AB	D	C F E H		G	K J
a		a	a	a	a
2P		Ðèñ. 4.46			2P
		Ðèñ. 4.46

∑

Y = 0;

∑

X = 0 ;

1 A − A:

B − B :

N2 3 ∑Y = 0;

N2 4

∑mom 3

= 0;

C − C :

N3−4 ∑Y = 0 ;

N3−5

∑mom 4

= 0;

D − D:

N 4−5

∑Y = 0 ;

N 4−6

∑mom 5

= 0;

(4.15)

E − E :

N5−6

∑Y = 0;

N5−7

∑mom 6

= 0;

F − F :

N6−7

∑Y = 0;

N6−8

∑mom 7

= 0;

7g G −G :

N7−8 ∑Y = 0;

N 7−9

∑mom 8

= 0 ;

8g H − H :

N8−9 ∑Y = 0;

N8−10

∑mom 9

= 0;

J − J :

N9−10 ∑Y = 0 ;

N9−11 ∑mom10 = 0;

10g K − K : N10−11 ∑Y = 0 .

Уравнение в Фроекциях сил рекомендуется применять тогда, когда нельзя составить уравнение в моментах.

Уравнение в моментах требует вычисления расстояния от точки приведения до линии действия усилия, а уравнение в проекциях сил – вычисления значений тригонометрических функций угла между осями стержней. Эти задачи решаются через значения координат узлов фермы (табл. 4.1) по формулам аналитической геометрии.

Таблица 4.1

Óçëû	1	2	3	4	5	6	7	8	9	10	11
Коорд-ты	1	2	3	4	5	6	7	8	9	10	11
Коорд-ты

X i , a	0	0,5	1	1,5	2	2,5	3	3,5	4	4,5	5
Y i , a	0	1	0	1	0	1	0	1	0	1	0

Вычисление расстояния d(k, i-j) от точки k с координатами (Xk , Yk ) до прямой, проходящей через точку i с координатами (Xi, Yi è) точку j, имеющую координаты (Xj , Y,j ) осуществляется по формуле:

d(k,i − j) = (Ai, j Xk + Bi, j Yk + Ci, j) / Ai2, j + Bi2, j ,

116

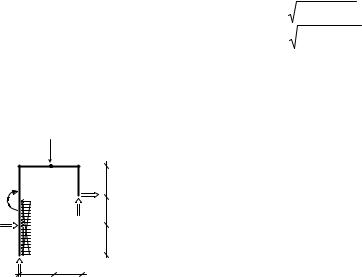
где использованы обозначения:

i, j

= − Y

−Y

i i

;

i, j

= X

− X

; C

i, j

= X

− X

d j

Тригонометрические функции углов между прямыми, проходящими через точки i-j è k-l, заданные своими координатами, определяются формулами:

tan(α i−j, k−l) =

Ai, j Bk,l

− Ak,l Bi, j

;

Ai, j Ak,l

+ Bi, j Bk,l

sin(α i−j, k−l) =

Ai, j Bk,l

− Ak,l Bi, j

;

Di,j Dk,l

cos(α i−j, k−l) =

Ai, j Ak,l

+ Bi, j Bk,l

Di,j Dk,l

где использованы обозначения

i, j

= − Y

−Y

i i

;

i, j

= X

− X

; D

i,j

= A2

+ B 2

;

d j

i, j

k,l

= − Y

−Y

k i

;

k,l

= X

− X

; D

k,l

= A2

+ B 2

d l

k,l

Положительный угол между прямыми определяется в результате поворота прямой i-j вокруг точки пересечения Фротив часовой стрелки до совмещения с прямой k-l.

Располагая системой нагрузок «в значениях», системой сечений (см. рис. 4.46), координатами узлов расчетной схемы (см. табл. 4.1) и форму-

	qa
	D	a
		a
2qa2	C XC
XB Ç	YC	a
XB Ç
0,5q
		a
A
YA a	a

Рис. 4.47 (начало)

лами для вычисления «плеч» сил при составлении уравнений моментов, можно приступать к непосредственному определению продольных усилий в стержнях заданной расчетной схемы фермы (рис. 4.47).

Важно отметить, что неизвестные усилия на рисунке отсеченной части расчетной схемы счи- таются положительными (действуют «от узла»), а их истинный («инженерный») знак устанавливается решением соответствующего уравнения:

∑

mom

= 0;

∑

mom

= 0;

(1)

∑

momслева =

∑

mom

сФрава = 0;

Xë

∑X = 0;

(2)

èëè XB

∑X = 0;

(2)

∑Y = 0.

(3)

∑Y = 0.

(3)

117

∑Y = 2P − 1 P − N2−3 cos β =
2
= 2P − 1 P − N2−3 0,894 = 0
2
N2−3 ≈ 1,68P(растяжение);
∑mom3 = −2P a + 1 P		1 a − N2−4h3, 2−4 =
	2	2
= −2P a + 1 P	1 a − N2−4 a = 0
2	2
N2−4 = −1,75P(сжатие);

		B-B
	P/2		B
		2	N2-4
3,2-4			N2-4
3,2-4			N2-3
h	1		N2-3
	1
0,5a		B P	3
0,5a
	2P	β
		á

∑Y = 2P −

1 P + N3−4 cos β =

= 2P − 1 P + N3 4 0,894 = 0

N3−4

≈ −168,P

(сжатие) ;

F 1

∑mom 4

a +

= −2P Ga +

P G

aJ +

+ N3−5 h4, 3−5 = −3P a +

1 P a +

+ N3−5 a = 0

N3−5

= 2,5P (растяжение) ;

∑Y = 2P −

1 P − P − N 4−5 cos β =

= 2P − 3 P − N 4−5 0,894 =

N4−5

≈

0,559P

(растяжение) ;

∑mom 5

= −2P ba + ag +

Ga +

aJ +

+ P 12 a − N 4−6 h5, 4−6 =

= −4P a + 54 P a − − N 4−6 a = 0

N4−6 = −2,75P (сжатие) ;

Рис. 4.47 (Фродолжение)

	C-C
	0,5a	β
	0,5P2	C 1,75P
5		4	N3-4
5
4,3-
h	1	3	N3-5
	1	3
		C
	a	0,5a
	2P
		â

D-D

	0,5a	a	P
	0,5P		P
	2		4 D N4-6
6				N4-5
5,4-				N4-5
5,4-	1	3	2,5P
h	1	3	2,5P
	a	D	a	β 5
	a		a

118

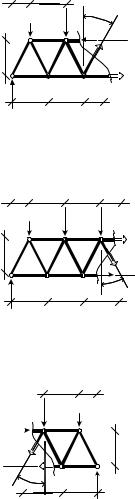
E-E

	0,5a			a	β
	0,5P				β
	0,5P			P E 2,75P			6
	2			4			6
7						N5-6
6,5-						N5-6
h	1		3	5				N5-7
	1		3	5
					0,5aE
		a		a	0,5aE
	2P			ä
				ä
				F-F
	0,5a			a	a	0,5a
	P/2			P		P
	P/2							N
	2			4	6	F		N	6-8
	2			4	6				6-8
7,6-8								N
h	1		3	5		3P		6-7
	1		3	5		3P		7
		a		a	F	a	β
		a		a		a
	2P			å
				å
				G-G
				a	0,5a
				P
2,75PG 8				H 10	P/2
	N8-7					8,7-9
		N9-7				h
		N9-7				11
	7β			G 9		11
	7β			G 9
			a		a
					2P

cos β ≈ 0,894;sin β ≈ 0,447 ; h 6, 5−7 = a ;

∑Y = 2P −		1 P − P + N			5−6 cos β =
		2
	= 2P −	3 P + N5−6 0,894 = 0
N5−6		2
N5−6	≈ −0,559P (сжатие) ;
∑mom 6		F	1	I	1
		H	2	K	2	P 2a +
	= −2P G2a +			aJ +		P 2a +

+P a + N5−7 h6,5−7 =

=−5P a + 2P a + N5−7 a = 0

N5−7 = 3P (растяжение) ;

cos β ≈ 0,894; sin β ≈ 0,447; h 7,6−8

= a;

∑Y = 2P −

1 P − P − P − N6−7 cos β =

= 2P −

5 P − N6−7 0,894 = 0

N6−7

≈ −0,559P

(сжатие) ;

∑mom 7

= −2P 3a +

P G2a

aJ +

− N6−8 h7, 6−8 =

+ P Ga +

aJ + P

= −6P a +

13 P a −

N6−8 a = 0

N6−8

= −2,75P (сжатие) ;

cos β ≈ 0,894; sin β ≈ 0,447; h8, 7−9

= a;

∑Y = 2P − 1 P − P − N8−7 cos

β =

= 2P −

3 P − N8−7 0,894 = 0

N8−7 ≈ 0,559P(растяжение);

∑mom8

P a − N9−7h8, 7−9 =

2P a +

a −

= 3P a −

1 P a − N9−7 a = 0

N9−7 = 2,5P(растяжение);

Рис. 4.47 (Фродолжение)

119

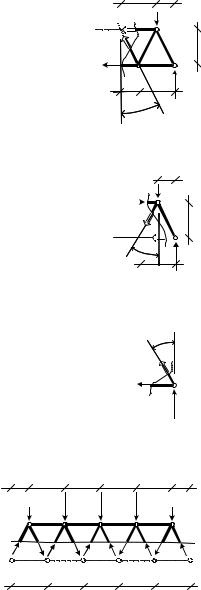
cos β ≈ 0,894; sin β ≈ 0,447; h 9,10−8 = a ;

∑Y = 2P − 12 P + N9−8 cos β =

=2P − 12 P + N9−8 0,894 = 0 N9−8 ≈ −168,P (сжатие) ;

∑mom 9	= 2P a −	1 P	1 a + N10− 8 h9,10−8 =
		2	2
	= 2P a −	1 P a + N10−8 a = 0
		4
N10−8	= −175,P (сжатие) ;

cos β ≈ 0,894; sin β ≈ 0,447; h10,11−9 = a;

∑Y = 2P −		1 P − N10−9 cos β =
		2
	= 2P −	1 P − N10−9 0,894 = 0
N10−9	≈ 168,P	2(растяжение) ;
∑mom10	= 2P 1 a − N11−9 h10,11−9 =
	2
	= 2P 1 a − N11−9 a = 0
	2
N11−9	= P (растяжение);
cos β ≈ 0,894;		sin β ≈ 0,447;

∑Y = 2P + N11−10 cos β =

=2P + N11−10 0,894 = 0 N11−10 ≈ −2,24P (сжатие) .

Рис. 4.47 (окончание)

H-H

	a	0,5a
N10-8 H		P/2
8		10
N9-8		-8
		9,10

2,5P	9	h
2,5P	9	11

0,5a a

β2P

	ç
	J-J
			0,5a
1,75PJ			P/2
			10
			-9
N10-9			10,11
N10-9		N11-9 h
9		N11-9 h
		β	J 11
			a
			2P

K-K

N11-10 K

ê 2P

Контроль правильности определения ординат продольных усилий для заданной расчетной схемы проводится для Фроизвольной части расчетной схемы (рис. 4.48). Соответствующие уравнения равновесия и вычисления по ним представлены формулами:

0,5a a							a				a						a				0,5a
0,5P							P				P					P		0,5P
2					4					6				8					10
	P						P				P 9				P						P
	P	6					5				P 9				P	6					,
4		P				P	9			9	P					P				P	4
4		,				P	,			9	5		9			,				P	2
,2		8			8		5		5							8			8		2
,2		1			8		0		5		5	5				1			8
2				6					5		,	,5							6
2			,					,			0	,5						,
1		3	1				5	0			7	0					9	1			11
1		3					5				7						9				11
		a					a				a					a					a
							Ðèñ. 4.48

120

∑Y =2,24P cos β − 0,5P −168,P cos β +168,P cos β − P −

−0,559P cos β + 0,559P cos β − P + 0,559P cos β −

−0,559P cos β − P +168,P cos β −168,P cos β −

−0,5P + 2,24P cos β =

=−4P + cos β b2,24 +168, + 0,559 + 0,559 +168, +2,24g − − b168, + 0,559 + 0,559 +168,g =

=−4P + 0,894 b8,96 − 4,48g =

=8,01 − 8,01 ≈ 0 ;

∑X =2,24P sin β +168,P sin β +168,P sin β +

+0,559P sin β + 0,559P sin β − 0,559P sin β −

− 0,559P sin β −168,P sin β −168,P sin β − 2,24P sin β =

				c				g
=	P sin β				2,24 +168,	+168, + 0,559+0,559			−
	b					g
−		0,559	+ 0,559 +168, +			168, + 2,24	=
	P sin β			b	g
=	P sin β				6,72 − 6,72	≈ 0;			(4.16)
									(4.16)

∑mom 1 = −0,5P 0,5a −168,P d(1, 2 − 3) +168,P d(1, 3 − 4) −

−P b0,5a + ag − 0,559P d(1, 4 − 5) + 0,559P d(1, 5 − 6) −

−P (0,5a + a + a) + 0,559P d(1, 6 − 7) − 0,559P d(1, 7 − 8) −

−P (0,5a + a + a + a) +168,P d(1, 8 − 9) −168,P d(1, 9 −10) −

−0,5P (0,5a + a + a + a + a) + 2,24P d(1,10 −11) =b0,5a + ag −

− 0,559P 179,a + 0,559P 179,a − P (0,5a + a + a) +

+0,559P 2,68a − 0,559P 2,68 − P (0,5a + a + a + a) +

+168,P 3,85a−,68P 3,58a − 0,5P (0,5a + a + a + a + a) +

+2,24P 4,47a =

= P a	b	0,894	+ 0,559		179, + 0,559 2,68 +
	1,68
+168, 3,85 + 2,24			g	−	b	0,5	+168, 0,894	+1 15, +
			4,47		0,5

+ 0,559 179, +1 2,5 + 0,559 2,68 +1 3,5 +168, 3,58 + 0,5 4,5) =

121

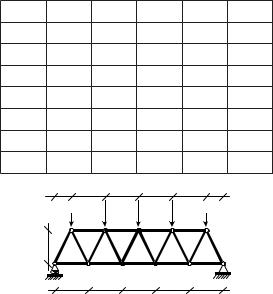
Уравнения равновесия отрезанной части заданной расчетной схемы удовлетворяются с относительной погрешностью, не превышающей 5%, что свидетельствует о значительной достоверности проведенных построений.

Следует обратить внимание на действия, обеспечивающие определенную точность вычислений, которые были проведены при решении задачи. В частности, окончательные результаты представлены с тремя значащими цифрами. Чтобы получить этот результат, промежуточные вычисления проводились с четырьмя значащими цифрами. Таким образом, в полученных результатах мы имеем не менее двух верных цифр, что обеспечивает погрешность вычислений не превышающую 5%.

Решение задачи об определении продольных усилий в ферме представлено табл. 4.2, построенной по данным рис. 4.47, и рис. 4.49.

						Таблица 4.2
i-j	N i j , P i-j		N i j , P i-j			N i j , P
1-2	–2,24	8-9	–1,68		4-6	–2,75
2-3	1,68	9-10		1,68	5-7	3,00
3-4	–1,68	10-11	–2,24		6-8	–2,75
4-5	0,559	1-3		1,00	7-9	2,50
5-6	–0,559	2-4	–1,75		8-10	–1,75
6-7	–0,559	3-5		2,5	9-11	1,00
7-8	0,559
	0,5a a	a		a	a 0,5a
	0,5P	P	P	P	0,5P
	2	4	6	8	10
	a
	1					11
	3	5		7	9
	a	a	a	a	a
		Ðèñ. 4.49

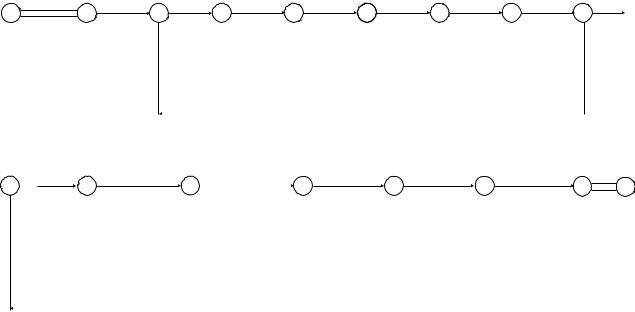
Операционный алгоритм, положенный основу решенной задачи, представлен на рис. 4.50. Рекомендуется провести анализ операций, которые в нем отображены, с целью их сравнения с операциями в алгоритме расчета трехшарнирной рамы.

122

Виды уравнений равновесия на плоскости.

Виды опорных связей, их изображения

[l k] = a; [P k] = P.

Рис. 4.41. Рис. 4.42.

Заданная Опорные расчетная стержни схема (ЗРС)

Глобальная

система

координат (ГСК)

Рис. 4.43. Рис. 4.44.

ДополниНагрузки тельные в обознанагрузки чениях

Ошибки в определении реакций

Оптимальный		Реакции
объем		определены
вычислений		верно
			*А
Ф. (4.13).	Рис. 4.45.	Ф. (4.14).	Рис. 4.46.
Система	Определение	Контроль	Нагрузки
уравнений	реакций	правильности	в значениях
для опорных	опорных	определения
реакций	связей	опорных
		реакций

		Поиск и исправление ошибок				Рис. 4.49,
					Усилия	табл. 4.2.
					Усилия	Решение
					определены	Решение
Рис. 4.46.					определены	задачи
	Рис. 4.46.				верно	задачи
	Рис. 4.46.				верно
*А
*А	Система сечений	Формулы	Рис. 4.47.	Ф. (4.16) ,	Табл. 4.2.
Номера	Система сечений	Формулы	Рис. 4.47.	Ф. (4.16) ,
Номера	для определения	для вычисления	Определение	рис. 4.48.
узлов-шарниров.	для определения	для вычисления	Определение	рис. 4.48.	Значения
Табл. 4.1.	продольных усилий.	расстояния от точки	продольных	Контроль	и знаки N i-j
Табл. 4.1.	Ф. (4.15).	до прямой	усилий N i-j	правильности	и знаки N i-j
Координаты	Ф. (4.15).	до прямой	усилий N i-j	правильности
Координаты	Система уравнений	и тригонометрических		определения
узлов фермы	Система уравнений	и тригонометрических		определения
	для определения Ni-j	функций угла		усилий
		между пересекающимися
		прямыми		Ошибки в определении усилий
				Ошибки в определении усилий

				Поиск и исправление ошибок

123

Ðèñ. 4.50

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 2610 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
08.05.201916.07 Mб30По алфавиту.doc
#
25.08.2019415.74 Кб3По Бачурской .doc
#
21.08.2019215.55 Кб11по гму. что-то типа лекций.doc
#
10.05.2015422.63 Кб37Погрузочная машина 1ППН5.docx
#
18.11.201970.14 Кб46Подготовка по связи т2.1.doc
#
16.03.20168.65 Mб87Полезная литература.pdf
#
10.05.201525.09 Кб9Полис.docx
#
13.07.201948.64 Кб1политич.система США.doc
#
04.11.2018218.62 Кб2Политическая конфликтология МУ - политологи.doc
#
08.11.2019190.98 Кб3Политическая конфликтология МУ - социологи.doc
#
11.11.2019204.8 Кб3Политическая социология рабочая программа.doc