Архитектура сети

Архитектура модифицированной сети Хопфилда представлена на рис. 8.5.

Рис. 8.5

Вход pустанавливает значения начальных условий. В сети используется линейная функция активации с насыщениемsatlins, которая описывается следующим образом:

(8.3)

Эта сеть может быть промоделирована с одним или большим количеством векторов входа, которые задаются как начальные условия. После того как начальные условия заданы, сеть генерирует выход, который по обратной связи подается на вход. Этот процесс повторяется много раз, пока выход не установится в положение равновесия. Можно надеяться, что каждый вектор выхода в конечном счете сойдется к одной из точек равновесия, наиболее близкой к входному сигналу.

Рассмотрим следующий пример. Предположим, что требуется разработать сеть с двумя устойчивыми точками в вершинах трехмерного куба:

T = [–1 –1 1; 1 –1 1]'

T =

–1 1

–1 –1

1 1

Выполним синтез сети:

net = newhop(T);

gensim(net)

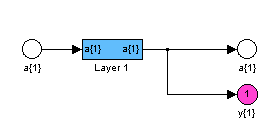
Структура сети представлена на рис. 8.6.

a	б
в

Рис. 8.6

Читателю следует обратить внимание, что на схеме рис.8.6, а вход и выход слоя совпадают; на рис.8.6, б показаны используемые в рекуррентном слое элементы. Обратимся к информации о структуре слоя:

net.layers{1}

ans =

dimensions: 3

distanceFcn: 'dist'

distances: [33 double]

initFcn: 'initwb'

netInputFcn: 'netsum'

positions: [0 1 2]

size: 3

topologyFcn: 'hextop'

transferFcn: 'satlins'

userdata: [11 struct]

Из этого списка следует, что в слое используется функция инициализации initwb, функция суммирования входов netsum и функция активации satlins.

На рис. 8.6, в показан блок, описывающий матрицу весов, которая определяет переходную матрицу динамической модели рекуррентного слоя.

Динамическая модель рекуррентного слоя модифицированной сети Хопфилда описывается следующим образом:

. (8.4)

При внимательном анализе приведенного соотношения можно действительно убедиться, что матрица весов LW¹¹равносильна переходной матрице динамической системы, а вектор смещенийb¹– вектору передачи единичного входа. Необходимо сформировать эти элементы, если заданы точки равновесия системыtв вершинах гиперкуба.

Синтез сети

Метод проектирования модифицированных сетей Хопфилда описан в работе [25], на основе этого метода разработан алгоритм синтеза, который реализован в ППП NTв виде подфункцииsolvehop2(t)М-функцииnewhop.

Если задано множество целевых точек равновесия, представленных матрицей T, то функцияnewhopвозвращает матрицу весов и вектор смещений для рекуррентного слоя сети Хопфилда. При этом гарантируется, что точки устойчивого равновесия будут соответствовать целевым векторам, но могут появиться и так называемые паразитные точки. В процессе синтеза сети число таких нежелательных точек сводится к минимуму.

Пусть задано Qцелевых векторов, образующих матрицуTразмераSQ:

(8.5)

Образуем новую матрицу YразмераSQ–1 следующего вида:

(8.6)

Вычислим разложение матрицы Yпо сингулярным числам:

(8.7)

Далее образуем матрицы

(8.8)

где K– ранг матрицыY.

Построим динамическую систему

, (8.9)

где T_ – матрица вида ТР – ТМ;  – динамический параметр (в алгоритме принят равным 10); E– единичная матрица.

Вычислим дискретную модель для системы (8.9):

, (8.10)

где Ф– переходная матрица вида;F– матрица передачи входа видас₁=e^h –1,c₂ = (1–e^–h)/;h– такт дискретности (в алгоритме принят равным 0.15c).

Соответствующая матрица весов рекуррентного слоя и вектор смещения вычисляются следующим образом:

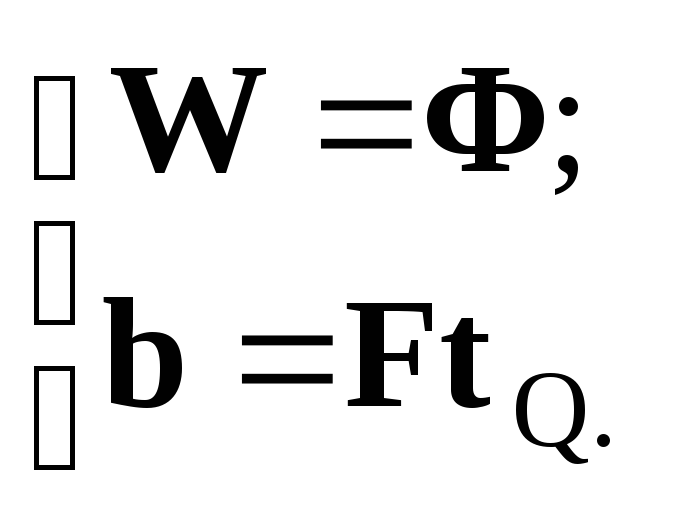(8.11)

Когда сеть спроектирована, она может быть проверена с одним или большим числом векторов входа. Весьма вероятно, что векторы входа, близкие к целевым точкам, равновесия найдут свои цели. Способность модифицированной сети Хопфилда быстро обрабатывать наборы векторов входа позволяет проверить сеть за относительно короткое время. Сначала можно проверить, что точки равновесия целевых векторов действительно принадлежат вершинам гиперкуба, а затем можно определить области притяжения этих точек и обнаружить паразитные точки равновесия, если они имеются.

Рассмотрим следующий пример. Предположим, что требуется создать модифицированную сеть Хопфилда с двумя точками равновесия, заданными в трехмерном пространстве:

T = [–1 –1 1; 1 –1 1]'

T =

–1 1

–1 –1

1 1

Выполним синтез сети, используя М-функцию newhop:

net = newhop(T);

Удостоверимся, что разработанная сеть имеет устойчивые состояния в этих двух точках. Выполним моделирование сети Хопфилда, приняв во внимание, что эта сеть не имеет входов и содержит рекуррентный слой; в этом случае целевые векторы определяют начальное состояние слоя Ai, а второй аргумент функции sim определяется числом целевых векторов:

Ai = T;

[Y,Pf,Af] = sim(net,2,[],Ai);

Y

Y =

–1 1

–1 –1

1 1

Действительно, устойчивые положения равновесия сети находятся в назначенных точках.

Зададим другое начальное условие в виде массива ячеек:

Ai = {[–0.9; –0.8; 0.7]};

Ai{1,1}

ans =

–0.9000

–0.8000

0.7000

Эта точка расположена вблизи первого положения равновесия, так что можно ожидать, что сеть будет сходиться именно к этой точке. При таком способе вызова функции sim в качестве второго параметра указываются такт дискретности и количество шагов моделирования:

[Y,Pf,Af] = sim(net,{1 5},{},Ai);

Y{1}

Y =

–1

–1

1

Действительно, из заданного начального состояния сеть вернулась в устойчивое положение равновесия. Желательно, чтобы сеть вела себя аналогичным образом при задании любой начальной точки в пределах куба, вершины которого составлены изо всех комбинаций чисел 1 и –1 в трехмерном пространстве. К сожалению, этого нельзя гарантировать, и достаточно часто сети Хопфилда включают нежелательные паразитные точки равновесия.

Пример:

Рассмотрим сеть Хопфилда с четырьмя нейронами и определим 4 точки равновесия в виде следующего массива целевых векторов:

T = [1 –1; –1 1; 1 1; –1 –1]'

T =

1 –1 1 –1

–1 1 1 –1

На рис. 8.7 показаны эти 4 точки равновесия на плоскости состояний сети Хопфилда.

plot(T(1,:), T(2,:),'*r') % Рис.8.7

axis([–1.1 1.1 –1.1 1.1])

title('Точки равновесия сети Хопфилда')

xlabel('a(1)'), ylabel('a(2)')

Рис. 8.7

Рассчитаем веса и смещения модифицированной сети Хопфилда, использую М-функ­цию newhop:

net = newhop(T);

W= net.LW{1,1}

b = net.b{1,1}

W =

1.1618 0

0 1.1618

b =

3.5934e–017

3.5934e–017

Проверим, принадлежат ли вершины квадрата к сети Хопфилда:

Ai = T;

[Y,Pf,Af] = sim(net,4,[],Ai)

Y =

1 –1 1 –1

–1 1 1 –1

Pf = []

Af =

1 –1 1 –1

–1 1 1 –1

Как и следовало ожидать, выходы сети равны целевым векторам.

Теперь проверим поведение сети при случайных начальных условиях:

plot(T(1,:), T(2,:),'*r'), hold on

axis([–1.1 1.1 –1.1 1.1])

xlabel('a(1)'), ylabel('a(2)')

new = newhop(T);

[Y,Pf,Af] = sim(net,4,[],T);

for i =1:25

a = {rands(2,1)};

[Y,Pf,Af] = sim(net,{1,20},{},a);

record = [cell2mat(a) cell2mat(Y)];

start = cell2mat(a);

plot(start(1,1), start(2,1), 'kx', record(1,:), record(2,:))

end

Результат представлен на рис. 8.8.

Рис. 8.8

Читатель может продолжить изучение модифицированных сетей Хопфилда, обратившись к демонстрационным примерам. Пример двумерной сети можно найти в демонстрации demohop1, пример неустойчивой точки равновесия – в демонстрацииdemohop2. Демонстрацияdemohop3дает пример трехмерной модифицированной сети Хопфилда.Демонстрация demohop4 иллюстрирует появление устойчивых паразитных точек равновесия.