
- •В. Г. Потемкин
- •Предисловие
- •Введение
- •Используемые обозначения
- •Часть 1. Ппп Neural Network Toolbox
- •1. Система matlab 6
- •1.1. Операционная среда matlab 6
- •Командное окно
- •Окно предыстории
- •Окно запуска
- •Окно текущего каталога
- •Окно рабочей области
- •Справочная подсистема
- •1.3. Демонстрационные примеры ппп nnt
- •2. Модель нейрона и архитектура сети
- •2.1. Модель нейрона
- •2.1.1. Простой нейрон
- •2.1.2. Функция активации
- •2.1.3. Нейрон с векторным входом
- •2.2. Архитектура нейронных сетей
- •2.2.1. Однослойные сети
- •2.2.2. Многослойные сети
- •2.2.3. Сети с прямой передачей сигнала
- •2.3. Создание, инициализация и моделирование сети Формирование архитектуры сети
- •Инициализация сети
- •Моделирование сети
- •3. Обучение нейронных сетей
- •3.1. Процедуры адаптации и обучения
- •Явление переобучения
- •Свойство обобщения
- •3.1.1. Способы адаптации и обучения
- •Адаптация нейронных сетей
- •Xlabel(''), ylabel('Выходыa(I)'),grid
- •Xlabel(''), ylabel('Весавходовw(I)'),grid
- •Xlabel(' Циклы'), ylabel('Ошибка'),grid
- •Xlabel(''), ylabel('Выходыa(I)'),grid
- •Xlabel(''), ylabel('Весавходовw(I)'),grid
- •Xlabel('Циклы'), ylabel('Ошибка'),grid
- •Xlabel(''), ylabel('Выходыa(I)'),grid
- •Xlabel(''), ylabel('Весавходовw(I)'),grid
- •Xlabel('Циклы'), ylabel('Ошибка'),grid
- •Обучение нейронных сетей
- •3.2. Методы обучения
- •3.2.1. Обучение однослойной сети
- •3.2.2. Обучение многослойной сети
- •Метод обратного распространения ошибки
- •Характеристика методов обучения
- •3.3. Алгоритмы обучения
- •3.3.1. Градиентные алгоритмы обучения Алгоритм gd
- •Алгоритм gdm
- •Алгоритм gda
- •Алгоритм Rprop
- •3.3.2. Алгоритмы метода сопряженных градиентов
- •Алгоритм cgf
- •Алгоритм cgp
- •Алгоритм cgb
- •Алгоритм scg
- •3.3.3. Квазиньютоновы алгоритмы Алгоритм bfgs
- •Алгоритм oss
- •Алгоритм lm
- •3.3.4. Алгоритмы одномерного поиска
- •Алгоритм gol
- •Алгоритм bre
- •Алгоритм hyb
- •Алгоритм cha
- •Алгоритм bac
- •3.3.5. Расширение возможностей процедур обучения
- •Переобучение
- •Метод регуляризации
- •Формирование представительной выборки
- •Предварительная обработка и восстановление данных
- •Пример процедуры обучения
- •4. Персептроны
- •4.1. Архитектура персептрона
- •4.2. Модель персептрона
- •Моделирование персептрона
- •Инициализация параметров
- •4.3. Процедуры настройки параметров
- •Правила настройки
- •Процедура адаптации
- •5. Линейные сети
- •5.1. Архитектура линейной сети
- •5.2. Создание модели линейной сети
- •5.3. Обучение линейной сети
- •Процедура настройки
- •Процедура обучения
- •5.4. Применение линейных сетей Задача классификации векторов
- •Фильтрация сигнала
- •Предсказание сигнала
- •Подавление шумов
- •Многомерные цифровые фильтры
- •6. Радиальные базисные сети
- •Модель нейрона и архитектура сети
- •Создание сети
- •Радиальная базисная сеть с нулевой ошибкой
- •Итерационная процедура формирования сети
- •Примеры радиальных базисных сетей
- •6.1. Сети grnn
- •Архитектура сети
- •Синтез сети
- •6.2. Сети pnn
- •Архитектура сети
- •Синтез сети
- •7. Сети кластеризации и классификации данных
- •7.1. Самоорганизующиеся нейронные сети
- •7.1.1. Слой Кохонена
- •Архитектура сети
- •Создание сети
- •Правило обучения слоя Кохонена
- •Правило настройки смещений
- •Обучение сети
- •7.1.2. Карта Кохонена
- •Топология карты
- •Функции для расчета расстояний
- •Архитектура сети
- •Создание сети
- •Обучение сети
- •Одномерная карта Кохонена
- •Двумерная карта Кохонена
- •Архитектура сети
- •Создание сети
- •Обучение сети Правила настройки параметров
- •Процедура обучения
- •8. Рекуррентные сети
- •8.1. Сети Элмана
- •Архитектура
- •Создание сети
- •Обучение сети
- •Проверка сети
- •8.2. Сети Хопфилда
- •Архитектура сети
- •Синтез сети
- •9. Применение нейронных сетей
- •9.1. Аппроксимация и фильтрация сигналов
- •9.1.1. Предсказание стационарного сигнала Постановка задачи
- •Синтез сети
- •Проверка сети
- •9.1.2. Слежение за нестационарным сигналом
- •Инициализация сети
- •Проверка сети
- •9.1.3. Моделирование стационарного фильтра
- •Постановка задачи
- •Синтез сети
- •Проверка сети
- •9.1.4. Моделирование нестационарного фильтра
- •Постановка задачи
- •Инициализация сети
- •Проверка сети
- •9.2. Распознавание образов
- •Постановка задачи
- •Нейронная сеть
- •Архитектура сети
- •Инициализация сети
- •Обучение
- •Обучение в отсутствие шума
- •Обучение в присутствии шума
- •Повторное обучение в отсутствие шума
- •Эффективность функционирования системы
- •9.3. Нейронные сети и системы управления
- •9.3.1. Регулятор с предсказанием
- •9.3.2. Регулятор narma-l2
- •9.3.3. Регулятор на основе эталонной модели
- •Часть2. Операторы, функции и команды
- •10. Вычислительная модель нейронной сети
- •10.1. Описание сети Описание архитектуры
- •Функции инициализации, адаптации и обучения
- •10.2. Описание элементов сети
- •Описание входов
- •Описание слоев
- •Описание выходов
- •Описание целей
- •Описание смещений
- •Описание весов входа
- •Описание весов слоя
- •Матрицы весов и векторы смещений
- •Информационные поля
- •11. Формирование моделей нейронных сетей
- •11.1. Модели сетей
- •11.1.1. Однослойные сети Персептрон
- •Линейные сети
- •11.1.2. Многослойные сети
- •Радиальные базисные сети
- •Самоорганизующиеся сети
- •Сети – классификаторы входных векторов
- •Рекуррентные сети
- •11.2. Функции активации
- •Персептрон
- •Линейные сети
- •Радиальные базисные сети
- •Самоорганизующиеся сети
- •Рекуррентные сети
- •11.3. Синаптические функции
- •Функции взвешивания и расстояний
- •Функции накопления
- •11.4. Функции инициализации
- •11.5. Функции адаптации и обучения Функции адаптации
- •Функции обучения
- •Градиентные алгоритмы обучения
- •Алгоритмы метода сопряженных градиентов
- •Квазиньютоновы алгоритмы обучения
- •11.5.1. Функции оценки качества обучения
- •11.6. Функции настройки параметров
- •11.6.1. Функции одномерного поиска
- •11.7. Масштабирование и восстановление данных
- •11.8. Вспомогательные функции
- •Утилиты вычислений
- •Операции с массивами данных
- •Графические утилиты
- •Информация о сети и ее топологии
- •11.9. Моделирование нейронных сетей и система Simulink Функции моделирования сети
- •11.9.1. Применение системы Simulink
- •Библиотеки блоков для моделирования нейронных сетей
- •Построение моделей нейронных сетей
- •Индексный указатель Команды, функции и операторы ппп Neural Network Toolbox
- •Предметный указатель
- •Литература Книги на английском языке:
- •Книги на русском языке:
- •Оглавление
5.1. Архитектура линейной сети
Модель нейрона. На рис. 5.1 показан линейный нейрон с двумя входами. Он имеет структуру, сходную со структурой персептрона; единственное отличие состоит в том, что используется линейная функция активацииpurelin.
 Рис. 5.1
Рис. 5.1
Весовая матрица Wв этом случае имеет только одну строку и выход сети определяется выражением
![]()
![]() Подобно
персептрону, линейная сеть задает в
пространстве входов разделяющую
линию,
на которой функция активацииn равна
0 (рис. 5.2).
Подобно
персептрону, линейная сеть задает в
пространстве входов разделяющую
линию,
на которой функция активацииn равна
0 (рис. 5.2).
![]()
 Рис. 5.2
Рис. 5.2
Векторы входа, расположенные выше этой линии, соответствуют положительным значениям выхода, а расположенные ниже – отрицательным. Это означает, что линейная сеть может быть применена для решения задач классификации. Однако такая классификация может быть выполнена только для класса линейно отделимых объектов. Таким образом, линейные сети имеют то же самое ограничение, что и персептрон.
Архитектура сети. Линейная сеть, показанная на рис. 5.3,а, включаетSнейронов, размещенных в одном слое и связанных сRвходами через матрицу весовW.

Рис. 5.3
На рис. 5.3, бпоказана укрупненная структурная схема этой сети, вектор выходаaкоторой имеет размерS1.
5.2. Создание модели линейной сети
Линейную сеть с одним нейроном, показанную на рис.5.1, можно создать следующим образом:
net = newlin([–1 1; –1 1],1);
Первый входной аргумент задает диапазон изменения элементов вектора входа; второй аргумент указывает, что сеть имеет единственный выход. Начальные веса и смещение по умолчанию равны 0.
Присвоим весам и смещению следующие значения:
net.IW{1,1} = [2 3];
net.b{1} =[–4];
Теперь можно промоделировать линейную сеть для следующего предъявленного вектора входа:
p = [5;6];
a = sim(net,p)
a = 24
5.3. Обучение линейной сети
Для заданной линейной сети и соответствующего множества векторов входа и целей можно вычислить вектор выхода сети и сформировать разность между вектором выхода и целевым вектором, которая определит некоторую погрешность. В процессе обучения сети требуется найти такие значения весов и смещений, чтобы сумма квадратов соответствующих погрешностей была минимальной. Эта задача разрешима, потому что для линейных систем функция квадратичной ошибки является унимодальной.
Как и для персептрона, применяется процедура обучения с учителем, которая использует обучающее множество вида:
![]() (5.1)
(5.1)
где
![]() – входы сети;
– входы сети;![]() – соответствующие целевые выходы.
– соответствующие целевые выходы.
Требуется минимизировать следующую функцию средней квадратичной ошибки:
![]() . (5.2)
. (5.2)
Процедура настройки
В отличие от многих других сетей настройка линейной сети для заданного обучающего множества может быть выполнена посредством прямого расчета с использованием М-функции newlind.
Предположим, что заданы следующие векторы, принадлежащие обучающему множеству:
P = [1 –1.2];
T = [0.5 1];
Построим линейную сеть и промоделируем ее:
net = newlind(P,T);
Y = sim(net, P);
Y = 0.5 1
net.IW{1,1}
ans = –0.22727
net.b
ns = [0.72727]
Выход сети соответствует целевому вектору.
Зададим следующий диапазон весов и смещений, рассчитаем критерий качества обучения и построим его линии уровня (рис. 5.4):
w_range=–1:0.1: 0; b_range=0.5:0.1:1;
ES = errsurf(P,T, w_range, b_range, 'purelin');
contour(w_range, b_range,ES,20)
hold on
plot(–2.2727e–001,7.2727e–001, 'x') % Рис.5.4.
hold off
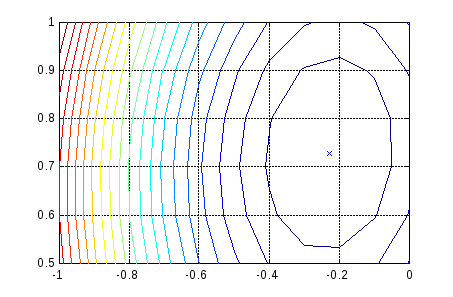 Рис. 5.4
Рис. 5.4
На графике знаком x отмечены оптимальные значения веса и смещения для данной сети.
Демонстрационный пример demolin1поясняет структуру линейной сети, построение поверхности ошибок и выбор оптимальных настроек.
Обучающее правило наименьших квадратов.Для линейной нейронной сети используется рекуррентное обучающее правило наименьших квадратов (LMS), которое является намного более мощным, чем обучающее правило персептрона. Правило наименьших квадратов, илиправило обучения WH (Уидроу – Хоффа), минимизирует среднее значение суммы квадратов ошибок обучения [18].
Процесс обучения нейронной сети состоит в следующем. Авторы алгоритма предположили, что можно оценивать полную среднюю квадратичную погрешность, используя среднюю квадратичную погрешность на каждой итерации. Сформируем частную производную по весам и смещению от квадрата погрешности на k-й итерации:
 (5.3)
(5.3)
Подставляя выражение для ошибки в форме
 , (5.4)
, (5.4)
получим
 (5.5)
(5.5)
Здесь pj(k) –j-й элемент вектора входа наk-й итерации. Эти соотношения лежат в основе обучающего алгоритма WH
 (5.6)
(5.6)
Результат может быть обобщен на случай многих нейронов и представлен в следующей матричной форме:
 (5.7)
(5.7)
Здесь ошибка eи смещениеb– векторы и– параметр скорости обучения. При больших значенияхобучение происходит быстро, однако при очень больших значениях может приводить к неустойчивости. Чтобы гарантировать устойчивость процесса обучения, параметр скорости обучения не должен превышать величины 1/max(||), где– собственное значение матрицы корреляцийp*pTвекторов входа. Используя правило обучения WH и метод наискорейшего спуска, всегда можно обучить сеть так, чтобы ее погрешность была минимальной.
М-функция learnwh предназначена для настройки параметров линейной сети и реализует следующее обучающее правило:
 (5.8)
(5.8)
где lr– параметр скорости обучения. Максимальное значение параметра скорости обучения, которое гарантирует устойчивость процедуры настройки, вычисляется с помощью М-функцииmaxlinlr.
С помощью демонстрационной программы demolin7можно исследовать устойчивость процедуры настройки в зависимости от параметра скорости обучения.
