
Дифференциальные уравнения 2
.pdf
дифференциального уравнения (16.2). На практике его можно найти, используя какие-либо из особенностей задания функций P и Q. Иногда его ищут в виде µ = µ(x) или в виде µ = µ(y). Тогда дифференциальное уравнение (16.2) для искомой функции µ упрощается.
Пример 16.1. Решите дифференциальное уравнение
2(x − y4)dy = ydx.
Решение. В данном случае P = y, Q = 2(y4 − x), ∂P∂y = 1 ≠ ∂Q∂x = −1. Нетрудно видеть, что y = 0 является решением нашего дифференциального уравнения. Пусть теперь y ≠ 0. Будем искать интегрирующий множитель в виде µ = µ(y). Из (16.1) имеем, что
−y∂µ∂y = 3µ.
Решением данного дифференциального уравнения служит, например, функция
1
µ = y3 .
После умножения исходного дифференциального уравнения
1
на y3 получаем уравнение в полных дифференциалах
()
1 |
|
dx + 2 y |
− |
x |
dy = 0. |
|||||||
|
|
|
|
|
||||||||
|
|
y2 |
y3 |
|||||||||
Отсюда |
|
|
|
|
|
|
|
|
|
|||
|
∂u |
1 |
|
∂u |
|
|
|
x |
||||
|
|
|
= |
|
, |
|
= 2(y − |
|
). |
|||
|
∂x |
y2 |
∂y |
y3 |
||||||||
Из первого уравнения имеем, что
x
u(x, y) = y2 + φ(y).
71

Подставляя u(x, y) во второе уравнение, получаем, что
φ′(y) = 2y,
откуда
φ(y) = y2 − C.
А поэтому все решения исходного дифференциального уравнения задаются формулами
yx2 + y2 = C, y = 0.
В некоторых случаях для решения дифференциальных уравнений (15.1) можно применять метод выделения полных диф-
ференциалов, используя известные формулы:
( )
d(xy) = ydx + xdy, d(yn) = nyn−1dy, d |
y |
= |
xdy − ydx |
, |
|
x |
x2 |
||||
|
|
|
и т.д.
Пример 16.2. Решите дифференциальное уравнение
ydx − (4x2y + x)dy = 0.
Решение. Нетрудно видеть, что x = 0 является решением данного дифференциального уравнения. Пусть x ≠ 0. Деля исходное дифференциальное уравнение на −x2, имеем, что
|
y |
|
y |
|
y |
|
||
d( |
|
) |
+ 4ydy = 0, d( |
|
) |
+ d(2y2) = 0, d( |
|
+ 2y2) = 0. |
x |
x |
x |
||||||
Последнее дифференциальное уравнение есть уравнение в полных дифференциалах. Оно имеет общее решение
xy + 2y2 = C.
72

Принимая во внимание случай x = 0, приходим к выводу, что все решения исходного дифференциального уравнения задаются формулами
xy + 2y2 = C, x = 0.
Если в дифференциальном уравнении (15.1) можно выделить полный дифференциал некоторой функции φ(x, y), то иногда данное дифференциальное уравнение упрощается, если от переменных (x, y) перейти к переменным (x, z) или
(z, y), где z = φ(x, y).
Пример 16.3. Решите дифференциальное уравнение
ydx − (x3y + x)dy = 0.
Решение. Нетрудно видеть, что x = 0 является решением данного дифференциального уравнения. Пусть x ≠ 0. Деля
исходное дифференциальное уравнение на −x2, имеем, что
( )
d |
y |
+ xydy = 0. |
|
x |
|||
|
|
Переходя к переменным z = xy и y, получаем дифференциальное уравнение (У–4)
dz + y2 dy = 0, z
которое нетрудно решить, как являющееся дифференциальным уравнением с разделяющимися переменными (см. § 18)
(У–5).
73
§ 17. Дифференциальные уравнения с разделенными переменными.
Дифференциальным уравнением с разделенными переменными будем называть дифференциальное уравнение вида
p(x)dx + q(y)dy = 0, |
(17.1) |
где функция p(x) непрерывна на (a, b), функция q(y) непрерывна на (c, d), область a < x < b, c < y < d, не содержит особых точек дифференциального уравнения (17.1).
Если существует параметрическое решение x = φ(t), y = ψ(t), t I, дифференциального уравнения (17.1), то подставив его в это дифференциальное уравнение, получим тождество
p(φ(t))dφ(t) + q(ψ(t))dψ(t) = 0, t I. |
(17.2) |
Замечание 17.1. В теории дифференциальных уравнений
∫
символом вида f(x)dx, где f(x) есть заданная непрерывная функция на некотором промежутке, принято обозначать
фиксированную первообразную, в отличие от математическо-
∫
го анализа, где символ f(x)dx обозначает множество всех
первообразных функции f(x).
∫
Пусть P (x) = p(x)dx∫есть какая–либо первообразная функции p(x), а Q(y) = q(y)dy есть некоторая первообразная функции q(y). Тогда интегрирование тождества (17.2) приводит к соотношению
P (φ(t)) + Q(ψ(t)) = C, t I,
где C есть произвольная постоянная. Поэтому всякое параметрическое решение дифференциального уравнения (17.1) удовлетворяет соотношению
∫ p(x)dx + ∫ q(y)dy = C |
(17.3) |
74
при некотором значении параметра C.
Нетрудно видеть, что если x = φ(t), y = ψ(t), t I, есть параметрическое задание гладкой кривой, удовлетворяющей на промежутке I уравнению (17.2) при некотором значении постоянной C, то оно определяет параметрическое решение при некотором значении дифференциального уравнения (17.1). Таким образом, если формула (17.3), где C есть произвольная постоянная, задает гладкую кривую при некотором значении C, то эта формула определяет некоторое параметрическое решение дифференциального уравнения (17.1) и содержит все параметрические решения этого дифференциального уравнения. В итоге приходим к выводу, что формула (17.3) определяет общий интеграл дифференциального уравнения (17.1).
Если необходимо найти интегральную кривую дифференциального уравнения (17.1), проходящую через точку (x0, y0), где x0 (a, b), y0 (c, d), то в силу формулы (17.3) такая кривая однозначно задается формулой
∫x ∫y
p(τ)dτ + q(η)dη = 0.
x0 y0
Пример 17.1. Решите уравнение
xdx + ydy = 0.
Решение. Применяя формулу (17.3), получаем общее решение исходного дифференциального уравнения
∫ |
xdx + ∫ |
|
C x2 2 C |
|||||||
ydy = |
|
, |
|
+ |
y |
= |
|
, x2 + y2 = C. |
||
2 |
2 |
2 |
2 |
|||||||
75

§ 18. Дифференциальные уравнения с разделяющимися переменными.
Дифференциальным уравнением с разделяющимися переменными будем называть дифференциальное уравнение вида
p1(x)q1(y)dx + p2(x)q2(y)dy = 0, |
(18.1) |
где функции p1(x) и p2(x) непрерывны на (a, b), а функции q1(y) и q2(y) непрерывны на (c, d), область G : a < x < b, c < y < d, не содержит особых точек дифференциального уравнения (18.1).
Если существует такое значение x0 (a, b), что p2(x0) = 0, то непосредственной проверкой убеждаемся, что x = x0 является решением дифференциального уравнения (18.1). Аналогичным образом убеждаемся, что если q1(y0) = 0 для некоторого значения y0 (c, d), то y = y0 также является решением дифференциального уравнения (18.1). Если же p2(x1) ≠ 0 и q1(y1) ≠ 0, то в некоторой окрестности точки (x1, y1) G дифференциальное уравнение (18.1) равносильно (т.е. у них одно и то же множество решений) уравнению с разделенными переменными
p1(x) dx + q2(y) dy = 0. p2(x) q1(y)
Теперь на основании формулы (17.3) получаем общий интеграл дифференциального уравнения (18.1) в окрестности точки (x1, y1) G:
∫ |
p1(x) |
∫ |
q2(y) |
|
||
|
dx + |
|
dy = C. |
(18.2) |
||
p2(x) |
q1(y) |
|||||
Если интегральные кривые семейства (18.2) касаются одной из прямых x = x0 или y = y0, то путем объединения
76
частей кривых (18.2) и частей прямых x = x0 и y = y0 в точках касания, получаем множество новых, так называемых составных, решений дифференциального уравнения (18.1).
Пример 18.1. Решите дифференциальное уравнение y′ =
√
3 3 y2.
Решение. Используя соотношение dy = y′dx, из исходного дифференциального уравнения получаем дифференциальное
уравнение в симметричной форме
√
dy = 3 3 y2dx.
Непосредственной проверкой убеждаемся, что y = 0 есть решение данного дифференциального уравнения. Предполагая, что y√≠ 0, разделим обе части дифференциального уравнения на 3 3 y2. В результате получим дифференциальное уравнение с разделенными переменными
dy
√ = dx.
3 3 y2
Отсюда находим, что √3 y = x + C или y = (x + C)3. Нетрудно проверить, что в точках (−C, 0) кривые y = (x + C)3 касаются прямой y = 0. В силу этого исходное дифференциальное уравнение, кроме решений
y = 0, y = (x + C)3,
имеет бесконечное множество составных решений, составленных из частей ранее полученных решений. Например, (см. рис. 18.1), это есть решения ABH, DBE, F GBE.
77
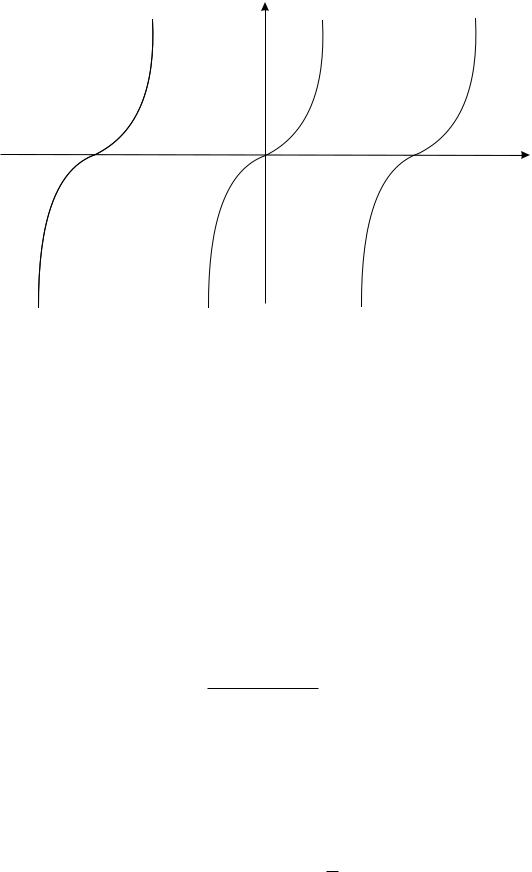
Y
D O G
F
E
B X
H
A
Рис. 18.1. Дифференциальное уравнение вида
y′ = f(ax + by + c),
где f(z) есть заданная непрерывная функция по своему аргументу на некотором промежутке, a, b, c есть заданные вещественные числа, a2 + b2 > 0, заменой z = ax + by + c приводится к дифференциальному уравнению с разделяющимися переменными (У–6)
z′ = a + bf(z).
Пример 18.2. Решите задачу Коши
√
y′ = 4x + 2y − 1, y(0) = 1.
Решение. После замены
z = 4x + 2y − 1
исходное дифференциальное уравнение примет вид
√
z′ = 4 + 2 z.
78

Его интегрирование дает выражение |
|
|
|
||
√ |
|
|
√ |
|
|
x + C = z − 2 ln(2 + |
|
z), |
|||
где C есть произвольная постоянная. Возвращаясь к переменной y, получим формулу всех решений исходного диффе-
ренциального уравнения
√ √
x + C = 4x + 2y − 1 − 2 ln(2 + 4x + 2y − 1).
Из начального условия находим, что
C = 1 − 2 ln 3.
Поэтому решение исходной задачи Коши задается формулой
√ √
x + 1 − 2 ln 3 = 4x + 2y − 1 − 2 ln(2 + 4x + 2y − 1).
79

§ 19. Линейные дифференциальные уравнения первого порядка.
Дифференциальное уравнение вида
y′ + p(x)y = f(x), |
(19.1) |
где p(x) и f(x) есть функции, непрерывные на (a, b), называется линейным дифференциальным уравнением первого порядка. Если в дифференциальном уравнении (19.1) f(x) ̸≡0 на (a, b), то данное дифференциальное уравнение называется неоднородным, а если f(x) ≡ 0 на (a, b), – то
однородным.
Рассмотрим сначала линейное однородное дифференциальное уравнение первого порядка
y′ + p(x)y = 0. |
(19.2) |
Нетрудно видеть, что y = 0 является решением этого дифференциального уравнения. Если же y ≠ 0, то дифференциальное уравнение (19.2) эквивалентно дифференциальному урав-
нению
dy
y
Данное уравнение является дифференциальным уравнением с разделенными переменными, а его решения определяются
формулой
∫x
ln |y| = − p(τ)dτ + lnC1,
x0
где x0 и x принадлежат интервалу (a, b), а C1 есть произвольная положительная постоянная. Вводя вспомогательное
80
