Дифференциальные уравнения 2

также является решением дифференциального уравнения (4.1). Оно войдет в общее решение этого дифференциального уравнения отдельным слагаемым.

Пример 4.5. Корнями характеристического уравнения (4.4) дифференциального уравнения (4.1) являются λ1 = λ2 =

λ3 = λ4 = 5, λ5 = λ6 = −3, λ7 = 9, λ8 = 0, λ9,10 = −2 ± 3i. Запишите общее решение этого дифференциального уравнения.

Решение. Согласно формулам (4.6), (4.11) и (4.15) имеем искомое общее решение:

x = C1e5t + C2te5t + C3t2e5t + C4t3e5t + C5e−3t + C6te−3t + C7e9t+ +C8 + C9e−2t cos 3t + C10e−2t sin 3t.

Если λ = α + iβ есть комплексный корень кратности k характеристического уравнения (4.4) дифференциального уравнения (4.1), то функции

tme(α+iβ)t = tmeαt cos βt + itmeαt sin βt, m = 0, k − 1, (4.16)

являются комплекснозначными частными решениями дифференциального уравнения (4.1). Отметим, что комплексно сопряженному корню λ = α − iβ в этом случае соответствует набор частных решений дифференциального уравнения (4.1), комплексно сопряженный набору (4.16).

Таким образом, паре комплексно сопряженных корней λ = α ± iβ характеристического уравнения (4.4) кратности k соответствуют 2k частных решений (4.16) дифференциального уравнения (4.1). Их линейная комбинация

x = C1eαt cos βt + C2teαt cos βt + . . . +

+Cktk−1eαt cos βt+

+Ck+1eαt sin βt + Ck+2teαt sin βt + . . . + (4.17) +C2ktk−1eαt sin βt

21

также есть решение этого дифференциального уравнения. Пример 4.6. Найдите общее решение дифференциального

уравнения

xV − 5xIV + 12xIII − 16xII + 12xI − 4x = 0.

Решение. Характеристическое уравнение

λ5 − 5λ4 + 12λ3 − 16λ2 + 12λ − 4 = (λ − 1)(λ2 − 2λ + 2)2 = 0

имеет корни λ1 = 1, λ2,3 = 1 ± i, λ4,5 = 1 ± i. Согласно (4.6)

и(4.17) имеем общее решение в виде

x = C1et + C2et cos t + C3tet cos t + C4et sin t + C5tet sin t.

22

§ 5. Фазовая плоскость однородного линейного дифференциального уравнения второго порядка с постоянными коэффициентами.

Рассмотрим однородное линейное дифференциальное уравнение второго порядка с постоянными коэффициентами

Согласно результатов предыдущего параграфа, в зависимости от корней характеристического уравнения

общее решение дифференциального уравнения (5.1) имеет вид:

Евклидову плоскость R2 = Oxy будем называть фазовой для дифференциального уравнения (5.1), если решение x = x(t) этого уравнения изображается на ней в виде фазовых графиков

x = x(t), y = y(t) = x′(t), t R.

Фазовый график стационарного решения, т.е. решения, сохраняющего постоянное значение при всех t, x = x(t) = ξ,

23

состоит из одной точки – точки покоя (ξ, 0). Графики нестационарных решений представляют собой параметрически заданные линии.

Непосредственными вычислениями проверяем, что сдвиг

x (t) = x(t − s) решения x также является решением дифференциального уравнения (5.1). Поэтому фазовые графики

решений x и x состоят из одних и тех же точек, т.е. совпадают. Отсюда имеем следующее утверждение.

Теорема 5.1. Два фазовых графика дифференциального уравнения (5.1) либо не имеют общих точек, либо совпадают.

В дальнейшем будем считать, что

Единственной точкой покоя дифференциального уравнения (5.1) является начало координат O(0, 0), т.к. вдоль стационарного решения x(t) = ξ выполняется

x′′(t) = x′(t) = 0, t R,

и на основании (5.1) имеем, что a0ξ = 0, а это в силу (5.6) влечет за собой ξ = 0. Говоря далее о фазовых графиках дифференциального уравнения (5.1), будем иметь в виду графики ненулевых решений этого дифференциального уравнения.

Т.к. y(t) = x′(t), то составляющая x(t) фазового графика возрастает в верхней полуплоскости y > 0 и убывает в нижней полуплоскости y < 0. Поэтому движение по фазовому графику при возрастании t в верхней полуплоскости происходит слева направо, а в нижней – справа налево. Касательная к графику в точке (x(t), y(t)) имеет угловой коэффициент

24

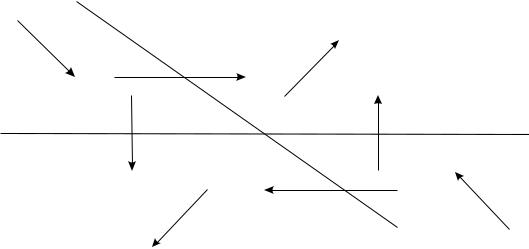
Поэтому каждый график пересекает ось y = 0 с вертикальной касательной, а прямую −a1y − a0x = 0 – с горизонтальной касательной. Так как вдоль фазового графика

то в полуплоскости −a1y −a0x < 0 составляющая y(t) убывает, а в полуплоскости −a1y − a0x > 0 – возрастает. Поэтому движение по фазовому графику при возрастании t в указанных полуплоскостях происходит вниз и вверх, соответственно (рис. 5.1).

- A1 Y - A0 X > 0

- A1 Y - A0 X < 0

- A1 Y - A0 X = 0

Рис. 5.1.

Непосредственными вычислениями убеждаемся, что при замене аргумента t на −t дифференциальное уравнение (5.1) переходит в уравнение (У–3)

При этом все фазовые графики отражаются симметрично относительно оси y = 0 и движение по графикам меняется на

25

противоположное. Взаимное же расположение графиков не меняется. Поэтому будем считать, что коэффициент

Фазовый график решения x будем называть O+-графи- ком, если (x(t), y(t)) → O при t → +∞.

y(t) x(t) →

k [−∞, +∞] = R∞ при t → +∞. Аналогично определяются O−- и kO−-графики. Если фазовый график дифференциального уравнения (5.1) является kO+- или kO−-графиком, то на основании правила Лопиталя и соотношения (5.7) при t → +∞ или t → −∞

= −a1 − a0 k.

Поэтому k ≠ ∞, и, учитывая (5.6), k ≠ 0. Таким образом, k2 + a1k + a0 = 0, т.е. k является корнем характеристического уравнения (5.2). В частности, при комплексно сопряженных корнях у дифференциального уравнения (5.1) не существует ни kO+-, ни kO−-графиков.

Рассмотрим случай, когда у характеристического уравнения (5.2) корни вещественные и при этом имеют различные знаки. В силу (5.3) на фазовом графике выполняются соотношения

x = C1eλ1t + C2eλ2t, y = λ1C1eλ1t + λ2C2eλ2t, λ1 < 0 < λ2.

Если

26

то график совпадает, соответственно, с лучом:

Он является λ1O+-графиком в случаях а) и б), и λ1O−-гра- фиком в случаях в) и г). если C1C2 ≠ 0, то график лежит между двумя лучами и уходит в бесконечность при t → +∞ и при t → −∞, имея асимптотой в первом случае λ1O−-луч,а

во втором – λ1O+-луч.

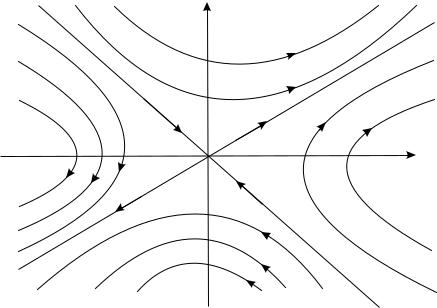
X

Y

O

Рис. 5.2.

Точка покоя с указанным расположением соседних фазовых графиков называется седлом (рис. 5.2). Отметим, что направление движения по графикам можно определить с помощью схемы на рис. 5.1.

Рассмотрим теперь случай, когда у характеристического уравнения (5.2) корни вещественны и имеют один знак. В силу (5.9) приходим к выводу, что они отрицательны. Если корни различны, то на основании (5.3) имеем, что

x = C1eλ1t + C2eλ2t, y = λ1C1eλ1t + λ2C2eλ2t, λ1 < λ2 < 0.

27

Нетрудно видеть, что фазовые графики являются O+-графи- ками. В случаях (5.10) графики оказываются лучами, расположенными во второй и четвертой четвертях. Если C1C2 ≠ 0, то

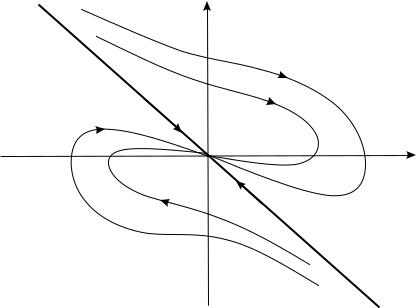
Поэтому график является λ2O+-графиком. При t → −∞ каждый график имеет асимптотой тот из лучей y = λ1x, x > 0, или y = λ1x, x < 0, который соответствует схеме на рис. 5.1. Точка покоя с таким расположением соседних фазовых графиков называется бикритическим узлом (рис. 5.3).

X

Y

O

Рис. 5.3.

Если же корни характеристического уравнения (5.2) совпадают, то в силу (5.4)

x = (C1 + C2t)eλt, y = ((λC1 + C2) + λC1t)eλt, λ < 0.

Фазовые графики являются O+-графиками. Так как для лю-

28

бого графика

то все они являются λO+-графиками. Точка покоя с таким расположением соседних фазовых графиков называется монокритическим узлом (рис. 5.4). При t → −∞ асимптотой для графика служит луч y = λx, x > 0, или луч y = λx, x < 0 (рис. 5.4).

X

Y

O

Рис. 5.4.

Пусть теперь у характеристического уравнения (5.2) корни комплексные: λ1,2 = α ± iβ, β ≠ 0.

Если α ≠ 0, то из (5.9) имеем, что α < 0. Поэтому фазовые графики в силу (5.5) имеют вид

и являются O+-графиками. Составляющие x(t) и y(t) бесконечно много раз меняют знак при t → ±∞. Поэтому график

29

представляет собой спираль, совершающую бесконечно много оборотов вокруг точки покоя O (рис. 5.5). Такую точку покоя

называют фокусом.

X

Y

O

Рис. 5.5.

X

Y

O

Рис. 5.6.

Если же α = 0, то на основании (5.11) имеем, что

x = C1 cos βt + C2 sin βt, y = −βC2 cos βt + βC1 sin βt.

30