Дифференциальные уравнения 2

и затем заменой z = a1x + b1y приведено (У–11) к дифференциальному уравнению с разделяющимися переменными.

91

§ 22. Дифференциальные уравнения первого порядка в общей форме.

Рассмотрим общий случай обыкновенного дифференциального уравнения первого порядка

не разрешенного относительно производной. Если же дифференциальное уравнение (22.1) удается разрешить относительно y′, то получаются дифференциальные уравнения вида

y′ = fi(x, y), i = 1, 2, . . .

которые могут быть проинтегрированы изложенными ранее методами.

Предположим, что дифференциальное уравнение (22.1) в окрестности точки (x0, y0) может быть разрешено относительно производной и распадается на дифференциальные уравнения

y′ = fi(x, y), i = 1, m.

Пусть каждое из этих уравнений имеет общее решение

или общий интеграл

Тогда совокупность общих решений (22.2) (или общих интегралов (22.3)) будем называть общим решением (общим интегралом) дифференциального уравнения (22.1).

Однако дифференциальное уравнение (22.1) не всегда разрешимо относительно производной y′ и еще реже полученные после этого дифференциальные уравнения

y′ = fi(x, y), i = 1, m,

92

интегрируются в квадратурах.

Рассмотрим интегрирование некоторых классов дифференциальных уравнений (22.1), не разрешенных относительно производных.

1. Уравнения, разрешенные относительно переменной y и не содержащие переменной x.

Эти дифференциальные уравнения имеют вид

Для интегрирования дифференциального уравнения (22.4) применим так называемый метод введения параметра. Положим y′ = p, где p есть параметр. Тогда дифференциальное уравнение (22.4) примет вид

Нам осталось получить еще одно уравнение, выражающее x через p и C. Оно получается таким образом. Так как y′ = p, то имеем, что

Применяя к последнему интегралу метод интегрирования по частям, с учетом (22.5) имеем, что

Таким образом, мы получили систему уравнений (22.5), (22.6), которая является общим решением дифференциального уравнения (22.4) в параметрической форме. Исключив,

93

если это возможно, из этой системы параметр p, получим общий интеграл дифференциального уравнения (22.4) в виде

Φ(x, y, C) = 0.

Пример 22.1. Найдите общее решение дифференциально-

Решение. Положив y′ = p, из дифференциального уравнения (22.7) имеем

y = ap2 + bp3 dy = 2apdp + 3bp2dp.

Далее с учетом того, что dy = pdx, получаем

pdx = 2apdp + 3b2dp dx = 2adp + 3bpdp,

и поэтому

x = 2ap + 32bp2 + C.

Следовательно, общим решением дифференциального уравнения (22.7) в параметрической форме будет система

{x = 2ap + 32bp2 + C, y = ap2 + bp3.

2.Уравнения, разрешенные относительно переменной x и не содержащие переменной y.

Данные дифференциальные уравнения имеют вид:

В данном случае положим y′ = p. Тогда

94

Далее используем соотношение y′ = p и формулу интегрирования по частям:

Система соотношений (22.9), (22.10) и является общим решением дифференциального уравнения (22.8) в параметрической форме. Если удается исключить из этой системы параметр p, то получим общий интеграл Φ(x, y, C) = 0 исходного дифференциального уравнения.

Пример 22.2. Найдите общее решение дифференциально-

=px + p cos p − sin p + C.

Витоге имеем общее решение дифференциального уравнения

(22.11) в параметрической форме

{

x = p sin p,

y= p2 sin p + p cos p − sin p + C.

3.Уравнения, разрешенные относительно переменной y.

Эти дифференциальные уравнения имеют вид

95

Дифференциальное уравнение (22.12) допускает параметрическое представление

С учетом соотношения dy = y′dx = pdx из (22.13) получаем дифференциальное уравнение, связывающее p и x:

Если дифференциальное уравнение (22.14) удается проинтегрировать в квадратурах, считая p функцией x (или x – функцией p), то, подставив общее решение p = a(x, C) (или общее решение x = b(p, C)) в соотношение y = φ(x, p), получим общее решение дифференциального уравнения (22.12) в виде

(или общее решение этого дифференциального уравнения в

параметрической форме)

{

x = b(p, C),

(22.16)

y = φ(b(p, C), p).

Пример 22.3. Найдите общее решение дифференциально-

Решение. Данное дифференциальное уравнение разрешено относительно переменной y. Оно допускает параметриче-

Так как dy = y′dx = pdx, то из (22.18) получаем, что

(−p+x)dx+(2p−x)dp = pdx (−2p+x)dx+(2p−x)dx = 0

96

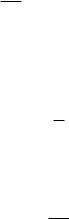
(2p − x)(−dx + dp) = 0.

Последнее уравнение распадается на два:

Первое из них дает

p = x + C.

Подставив данное выражение для p в (22.18), получим, что

y = x2 + Cx + C

2

есть общее решение дифференциального уравнения (22.17). Второе уравнение из (22.19) дает

x = p2.

Тогда из (22.18) получим решение

y = x2 .

4

4. Уравнения, разрешенные относительно переменной x.

Данные дифференциальные уравнения имеют вид

Оно допускает параметрическое представление в виде

Если дифференциальное уравнение (22.22) интегрируется в квадратурах, то дифференциальное уравнение (22.20) аналогично предыдущему случаю также может быть проинтегрировано в квадратурах.

97

5. Уравнение Лагранжа.

Данное уравнение имеет вид

Оно линейно относительно x и y, а φ и ψ есть заданные гладкие функции, причем φ(y′) ≠ y′, y = y(x).

Интегральные кривые этого дифференциального уравнения будем искать в параметрической форме x = x(p), y = y(p), где p есть параметр, в качестве которого возьмем y′ = p = p(x). Тогда из (22.23) имеем, что

Для нахождения зависимости x = x(p) продифференцируем соотношение (22.24) по x:

Дифференциальное уравнение (22.26) является линейным относительно x. Решив его, получим общее решение в виде x = x(p, C).

Таким образом, интегральные кривые уравнения Лагран-

жа (22.23) параметрически определяются системой

{

x = x(p, C),

(22.27)

y = x(p, C)φ(p) + ψ(p).

При переходе от дифференциального уравнения (22.25) к дифференциальному уравнению (22.26) пришлось делить на

98

dxdp. При этом могут теряться решения, для которых p посто-

янно, а, значит, dxdp = 0. Считая p постоянным, получаем, что дифференциальное уравнение (22.25) удовлетворяется лишь в том случае, если p есть корень уравнения

Таким образом, если p = pi есть вещественные корни уравнения (22.28), то к найденным выше решениям (22.27) надо

Уравнение Клеро является частным случаем уравнения Лагранжа.

Положим y′ = p. Тогда y = xp + ψ(p). Дифференцируя это соотношение по x, получаем, что

p = p + xdxdp + ψ′(p)dxdp (x + ψ′(p))dxdp = 0.

Отсюда или dxdp = 0, а, значит p = C; или x + ψ′(p) = 0.

В первом случае получаем однопараметрическое семейство

являющееся общим решением уравнения Клеро. Оно найдено без квадратур.

99

Во втором случае решение определяется в параметриче-

Пример 22.4. Найдите общее решение дифференциального уравнения

(22.33)

Решение. Заменяя y′ на C, получаем общее решение дифференциального уравнения (22.33) в виде

y = Cx + C2.

Решение вида (22.32) имеет вид

y = −x2 .

4

100