
Дифференциальные уравнения 2
.pdf
зываемые сложные точки покоя, которые можно рассматривать как результат слияния точек покоя основных типов. Главная же особенность нелинейных дифференциальных систем состоит в том, что помимо точек покоя, структура семейства траекторий системы определяется расположением и характером некоторых специальных траекторий, среди которых основную роль играют различные циклы, составленные из траекторий, и прежде всего – предельные циклы. Если рассматривать дифференциальную систему (33.1) как поле скоростей переноса массы на плоскости R2, то (при равномерном начальном распределении массы по плоскости) с течением времени t масса сосредотачивается около устойчивых точек покоя и устойчивых предельных циклов.
В настоящее время в основе многих естественных и технических теорий (прежде всего – в основе радиофизики и электроники) лежит математическая теория колебаний, которая базируется на математических моделях колебательных контуров, представляющих собой дифференциальные системы вида (33.1) в случае свободных колебаний или неавтономные дифференциальные системы, содержащие периодические по t слагаемые, – в случае вынужденных колебаний. При этом устойчивый свободный колебательный режим с заданной частотой и амплитудой колебания осуществим только в нелинейной дифференциальной системе с предельным циклом.
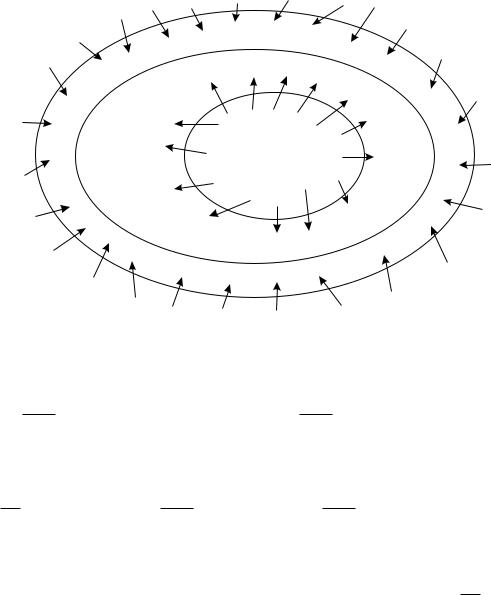
Одним из специальных приемов обнаружения предельного цикла является принцип кольца, предложенный Пуанкаре. Если удается построить кольцо K, ограниченное двумя гладкими кривыми Lk, k = 1, 2, такое, что на K нет точек покоя и все траектории пересекают Lk, входя (выходя из) K, то внутри K есть по крайней мере один предельный цикл (рис. 33.1). Этот принцип является непосредственным следствием
161
теоремы 33.6 (Пуанкаре–Бендиксона).
L2
L1
Рис. 33.1.
Пример 33.1. Рассмотрим дифференциальную систему dxdt1 = x2 − x1(x21 + x22 − 1), dxdt2 = −x1 − x2(x21 + x22 − 1).
Для нее выполняется соотношение
dtd (x21+x22) = 2x1 dxdt1 +2x2(x21+x22)dxdt2 = −2(x21+x22)(x21+x22−1).
Поэтому окружность x21 + x22 = 1 является циклом исследуе-
d
мой дифференциальной системы. Выражение dt(x21 + x22) положительно на окружностях
L1 : x21 + x22 = r, 0 < r < 1,
и отрицательно на окружностях
L2 : x21 + x22 = r, r > 1.
Поэтому траектории входят в круговое кольцо, ограниченное окружностями L1 и L2. По принципу кольца наша дифференциальная система имеет предельный цикл – окружность
x21 + x22 = 1. Этот предельный цикл устойчив (рис. 33.2).
162
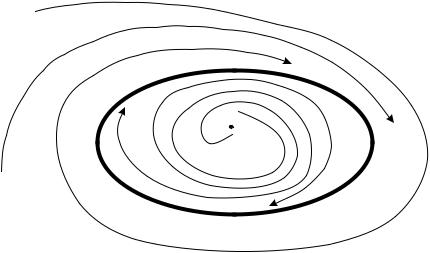
Рис. 33.2.
При переходе к дифференциальным системам в Rn, n > 2, роль предельных циклов начинают играть предельные торы и более сложные геометрические поверхности. Задача исследования предельных торов аналитическими средствами существенно усложняется. Аналитический аппарат можно эффективно использовать лишь в отдельных случаях.
163

§ 34. Линейные и квазилинейные уравнения в частных производных первого порядка.
В математике и ее приложениях наряду с обыкновенными дифференциальными уравнениями ведущую роль играют уравнения в частных производных. В математической физике, например, уравнения в частных производных второго порядка служат основным средством моделирования естественных процессов. Уравнения в частных производных первого порядка наряду с приложениями в геометрии имеют важное значение в газовой динамике и других областях прикладной математики. Вместе с тем уравнения в частных производных первого порядка являются вспомогательным аппаратом при исследовании уравнений в частных производных второго порядка.
Уравнение в частных производных первого порядка для
одной неизвестной функции u имеет вид |
|
|
|
|
|
||||
|
∂u |
∂u |
|
∂u |
|
∂u |
|||
F (x, u, |
|
) = 0, x = (x1, . . . , xn), |
|
|
=( |
|
, . . . , |
|
). |
∂x |
∂x |
∂x1 |
∂xn |
||||||
Решением, а также интегралом или интегральной поверхностью уравнения в частных производных первого порядка будем называть дифференцируемую функцию
u : E → R, E Rn,
обращающую данное уравнение в тождество на области E. Имеет место следующее утверждение.
Теорема 34.1 (Коши–Ковалевской). Пусть функции
φ(x2, . . . , xn) и f(x, u, p2, . . . , pn) голоморфны соответственно в окрестностях точек (ξ2, . . . , ξn) и (ξ1, . . . , ξn, η, ρ2, . . . , ρn), причем
η = φ(ξ2, . . . , ξn), ρi = φxi (ξ2, . . . , ξn), i = 2, n.
164
Тогда уравнение первого порядка, разрешенное относительно
∂u |
: |
|
|
|
|
|
|
|
|
|
|
|
|
||
∂x1 |
|
|
|
|
|
||
|
|
∂u |
|
∂u |
|
∂u |
|
|
|
|
= f(x, u, |
|
, . . . , |
|
) |
|
|
∂x1 |
∂x2 |
∂xn |
|||
имеет (и притом единственное) решение u = u(x), x E,
голоморфное в окрестности (ξ1, . . . , ξn) с начальным значением
u(ξ1, x2, . . . , xn) = φ(x2, . . . , xn).
Уравнение в частных производных первого порядка называют квазилинейным, если его можно представить в виде
f(x, u) |
∂u |
= g(x, u). |
(34.1) |
|
∂x |
||||
|
|
|
Иногда квазилинейные уравнения также называют неоднородными линейными уравнениями.
Уравнение в частных производных первого порядка назы-
вают линейным, если оно линейно относительно u и |
∂u |
, т.е. |
|||||
∂x |
|||||||
|
|
|
|
|
|
||
f(x) |
∂u |
+ g(x)u = h(x), |
|
|
|||
|
|
|
|||||
|
∂x |
|
|
||||
и однородным линейным, если h = g = 0, т.е. |
|
|
|||||
|
f(x) |
∂u |
= 0. |
(34.2) |
|||
|
|
||||||
|
|
|
∂x |
|
|
||
Во всех остальных случаях уравнение в частных производных первого порядка называют нелинейным.
Из теоремы о первом интеграле дифференциальной систе-
мы |
|
|
|
|
dx |
= f(x), x Rn, |
(34.3) |
|
dt |
||
|
|
165 |
|

следует, что функция u = Φ(x) является решением однородного линейного уравнения в частных производных первого порядка (34.2) в том и только том случае, если она есть первый интеграл дифференциальной системы (34.3). Пусть функции Φ1, . . . , Φm являются автономными (стационарными) первыми интегралами дифференциальной системы (34.3). Тогда каждая из функций u = H(Φ1, . . . , Φm) также служит первым интегралом для дифференциальной системы (34.3), и поэтому является решением дифференциального уравнения (34.2).
Следовательно, знание совокупности первых интегралов дифференциальной системы (34.3), соответствующей дифференциальному уравнению (34.2), позволяет получить общее решение (т.е. выражение, содержащее произвольную функцию) этого дифференциального уравнения. Отметим, что вместо дифференциальной системы (34.3) для интегрирования дифференциального уравнения (34.2) можно использовать соответствующую дифференциальную систему в симметрической форме
|
|
|
|
|
dx1 |
|
|
= . . . = |
|
dxn |
|
. |
(34.4) |
|||
|
|
|
f |
(x |
, . . . , x |
) |
f |
(x |
, . . . , x |
) |
||||||
|
1 |
1 |
|
n |
|
|
|
|
n |
1 |
n |
|
|
|
||
Пример 34.1. Дифференциальному уравнению |
|
|||||||||||||||
x2 |
∂u |
+ x1 |
∂u |
+ x2x3 |
∂u |
= 0, x1 > 0, x2 > 0, x3 > 0, |
||||||||||
|
|
|
||||||||||||||
|
∂x1 |
∂x2 |
|
∂x3 |
|
|
|
|
|
|||||||
соответствует дифференциальная система в симметрической
форме
dx1 = dx2 = dx3 , x2 x1 x2x3
независимыми первыми интегралами которой являются
Φ1 = x21 − x22, Φ2 = x1 − ln x3.
166

Поэтому выражение
u= H(x21 − x22, x1 − ln x3)
спроизвольной дифференцируемой функцией H является общим решением исходного уравнения в частных производных первого порядка.
Рассмотрим линейное однородное дифференциальное уравнение (34.2) с начальным условием
u|x1=ξ = φ(x2, . . . , xn). |
(34.5) |
Пусть Φ1(x1, . . . , xn), . . . , Φn−1(x1, . . . , xn) есть первые интегралы, образующие базис первых интегралов дифференциальной системы в симметрической форме (34.4). Тогда общее решение дифференциального уравнения (34.2) задается соотношением
u= H(Φ1, . . . , Φn−1)
идля выполнения начального условия (34.5) функцию H следует подобрать таким образом, чтобы было выполнено соотношение
H(Φ1(ξ, x2, . . . , xn), . . . , Φn−1(ξ, x2, . . . , xn)) = φ(x2, . . . , xn).
Составим систему функциональных уравнений
Φ1(ξ, x2, . . . , xn) = C1,
. . . . . . . . . . . . . . . . . . . . . . . . . . . (34.6) Φn−1(ξ, x2, . . . , xn) = Cn−1.
Из этой системы находим
xi = xi(ξ, C1, . . . , Cn−1), i = 2, n. |
|
Положим теперь |
|
H(C1, . . . , Cn−1) = φ(x2(ξ, C1, . . . , Cn−1), . . . , |
(34.7) |
xn(ξ, C1, . . . , Cn−1)). |
|
167
При таком определении функции H функция
u = u(x1, . . . , xn) = (34.8) = H(Φ1(x1, . . . , xn), . . . , Φn−1(x1, . . . , xn)),
являющаяся решением дифференциального уравнения (34.2), удовлетворяет и начальному условию (34.5), так как
u(ξ, x2, . . . , xn) = H(Φ1(ξ, x2, . . . , xn), . . . ,
Φn−1(ξ, x2, . . . , xn)) = H(C1, . . . , Cn−1) = φ(x2, . . . , xn).
Таким образом, построение решения дифференциального уравнения (34.2) с начальным условием (34.5) проводится по следующей схеме:
1)находим базис первых интегралов дифференциальной системы в симметрической форме (34.4), соответствующей исходному дифференциальному уравнению (34.2);
2)составляем систему функциональных уравнений (34.6), которую разрешаем относительно переменных x2, . . . , xn;
3)строим функцию H по формуле (34.7);
4)выписываем исходное решение по формуле (34.8) и, если это возможно, проводим аналитическое упрощение полученного решения.
Пример 34.2. В соответствии с указанной схемой найдем решение дифференциального уравнения примера 34.1, удовлетворяющее начальному условию
|
u|x1=1 = x22 + x32, |
|
||
следующим образом: |
|
|
|
|
{ |
Φ1(1, x2, x3) = C1, |
1 − x22 = C1, |
|
|
Φ2(1, x2, x3) = C2. |
{ 1 − ln x3 = C2. |
|||
|
x22 |
= 1 − C1, |
|
|
|
{ x3 |
= exp(1 − C2). |
|
|
168
Поэтому
H(C1, C2) = 1 − C1 + exp(2(1 − C2)),
и, следовательно,
u = u(x1, x2, x3) = 1 −Φ1(x1, x2, x3) + exp(2(1 −Φ2(x1, x2, x3))),
то есть
u = u(x1, x2, x3) = 1 − x21 + x22 + x23exp(2(1 − x1)).
Рассмотрим теперь линейное однородное уравнение с частными производными первого порядка, у которого искомая
функция z зависит от двух аргументов x и y: |
|
||||
f(x, y) |
∂z |
+ g(x, y) |
∂z |
= 0, (x, y) G R2. |
(34.9) |
|
|
||||
∂x |
∂y |
||||
Для дифференциального уравнения (34.9) построим соответствующую дифференциальную систему в симметрической форме:
dx |
= |
dy |
. |
(34.10) |
f(x, y) |
|
|||
|
g(x, y) |
|
||
Характеристикой дифференциального уравнения (34.9) будем называть линию K в пространстве R3 = Oxyz, заданную в виде
Φ(x, y) = C, x = γ,
где функция Φ(x, y), Φ : G → R, является первым интегралом дифференциальной системы (34.10); C и γ есть постоянные, причем C содержится во множестве значений функции Φ на G. Решение z = H(Φ(x, y)) дифференциального уравнения (34.9) задает в пространстве Oxyz интегральную поверхность Π. Через точку (ξ, η, ζ), где ζ = H(Φ(ξ, η)), проходит характеристика K дифференциального уравнения (34.9):
Φ(x, y) = Φ(ξ, η), z = ζ,
169

целиком расположенная на интегральной поверхности Π. Таким образом, интегральная поверхность дифференциального уравнения (34.9) состоит из характеристик этого дифференциального уравнения. Верно и обратное: любая поверхность в пространстве Oxyz, составленная из характеристик дифференциального уравнения (34.9), является интегральной поверхностью этого дифференциального уравнения. Для построения интегральной поверхности дифференциального уравнения (34.9), проходящей через заданную в пространстве Oxyz линию L, следует через каждую точку линии L провести характеристику дифференциального уравнения (34.9). Если L не касается ни одной характеристики дифференциального уравнения, то построенная поверхность невырожденная и действительно является искомой интегральной поверхностью.
Пример 34.3. Характеристиками дифференциального
уравнения
y∂x∂z + x∂y∂z = 0
являются линии
x2 − y2 = C, z = γ.
Если через каждую точку параболы
y = 1, z = 1 + x2
провести характеристику
z = γ, x2 − y2 = γ − 1,
то возникает гиперболический параболоид
z = 2 + x2 − y2,
который будет интегральной поверхностью исходного дифференциального уравнения.
170
