Дифференциальные уравнения 2

Для этого в формуле (9.14) положим t = t0 и x = x0. Далее подставив найденное значение C(t) в формулу (9.14), находим решение задачи Коши (9.15) в виде

Формула (9.16) носит название формулы Коши.

51

§ 10. Системы линейных дифференциальных уравнений с постоянными коэффициентами.

где aij R, i = 1, n, j = 1, n, будем называть однородной линейной системой обыкновенных дифференциальных уравнений с постоянными коэффициентами.

Введем матрицу A = ||aij||n×n и вектор-столбец неизвестных функций x = (x1, . . . , xn)T . С их помощью система (10.1) записывается в векторном виде

Часто система (10.2) интегрируется путем сведения к однородному линейному дифференциальному уравнению более высокого порядка, причем это дифференциальное уравнение будет также линейным с постоянными коэффициентами. Однако можно и непосредственно найти фундаментальную систему решений системы (10.1).

Одним из таких методов является метод Эйлера. В соответствии с этим методом нетривиальное решение системы (10.1) ищется в виде

где неизвестные числа γ1, . . . , γn, подлежат определению. В векторной записи решения (10.3) имеют вид

52

где γ = (γ1, . . . , γn)T .

Подставляя (10.4) в (10.2), затем сокращая на eλt и перенося все члены в левую часть равенств, получаем систему линейных однородных алгебраических уравнений относительно

γ1, . . . , γn:

(a11 − λ)γ1 + a12γ2 + . . . + a1nγn = 0,a21γ1 + (a22 − λ)γ2 + . . . + a2nγn = 0,

· · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·

an1γ1 + an2γ2 + . . . + (ann − λ)γn = 0,

или в векторной записи:

(A − λI)γ = 0,

где I есть единичная матрица размера n × n.

На основании системы (10.6) делаем следующий вывод: чтобы вектор-функция (10.4) была решением системы (10.2), необходимо и достаточно, чтобы λ и γ были, соответственно, собственным значением и собственным вектором матрицы A. Для отыскания собственных значений матрицы A необходимо решить уравнение

называемое характеристическим уравнением системы (10.2). В его левой части стоит многочлен n–ой степени с вещественными коэффициентами. Он называется характеристическим многочленом системы (10.2).

Характеристическое уравнение (10.7) имеет ровно n корней (с учетом их кратности). При этом возможны следующие случаи: 1) корни характеристического уравнения вещественны и различны; 2) корни характеристического уравнения различные, но среди них имеются комплексные; 3) среди корней характеристического уравнения имеются кратные. Рассмотрим каждый из этих случаев по отдельности.

53

Случай 1. Корни характеристического уравнения вещественны и различны. В этом случае матрица A имеет n линейно независимых собственных векторов γ1, . . . , γn, где

γ1 = (γ11, . . . , γn1)T , . . . , γn = (γ1n, . . . , γnn)T .

Тогда согласно (10.3) решениями системы (10.2) являются вектор–функции

Согласно теореме 9.2 функции (10.8)линейно независимы, т.е. образуют фундаментальную систему решений системы (10.2). Тогда общее решение этой системы имеет вид

Случай 2. Корни характеристического уравнения различные, но среди них имеются комплексные. Пусть одним из комплексных корней является λ = α + i β, β ≠ 0. Так как коэффициенты характеристического уравнения есть вещественные числа, то и λ = α − i β также будет корнем этого уравнения. Отвечающие этим двум корням λ и λ соответствующие собственные векторы также имеют комплексно сопряженные координаты, что следует из равенств

Aγ = λγ, Aγ = λγ

(т.к. в силу вещественности A = A).

Пусть γ = u + i v есть собственный вектор, соответствующий собственному значению λ = α + i β. Тогда согласно (10.3) вектор–функция

x = γeλt = (u + i v)e(α+i β)t

является решением системы (10.2). Применив формулу Эйлера, получим комплекснозначное решение системы (10.2) в

54

Как и в случае линейных однородных дифференциальных уравнений, показывается, что по отдельности действительная

(u cos βt − v sin βt)eαt и мнимая (v cos βt + u sin βt)eαt части комплекснозначного решения являются решениями системы (10.2).

Итак, мы получили, что паре комплексно сопряженных корней λ1,2 = α ± i β характеристического уравнения соответствует пара вещественных вектор–решений системы (10.2):

3. Среди корней характеристического уравнения имеются кратные (вещественные или комплексные).

Пусть среди корней характеристического уравнения имеется k–кратный корень λ (вещественный или комплексный). Ему соответствует решение

где каждая компонента Pik−1(t), i = 1, n, есть многочлен степени не выше k − 1 с постоянными коэффициентами, пока не определенными. Они находятся методом неопределенных коэффициентов. Отметим, что в случае комплексного корня λ аналогично пункту 2 на основании комплекснозначного решения (10.12) путем выделения его действительной и мнимой частей получаем вещественные решения.

Как мы показали в предыдущем параграфе, линейные неоднородные системы дифференциальных уравнений можно решить (если известна фундаментальная система решений со-

55

ответствующей линейной неоднородной системы) методом вариации произвольных постоянных (методом Лагранжа). Однако в частных случаях для нахождения общего решения можно использовать теорему 9.5 и метод неопределенных коэффициентов. Рассмотрим линейную неоднородную систему дифференциальных уравнений со специальной правой частью

α и β есть заданные вещественные числа, Pl(t) и Qm(t) есть вектор–функции, компонентами которых являются многочлены по переменной t со степенями, равными или меньшими, соответственно, l и m. В этом случае частное решение неоднородной системы (10.13) нужно искать в виде

где Rq+s(t) и Tq+s(t) есть вектор–функции, компонентами которых являются многочлены степени q+s с неопределенными пока коэффициентами,

q = max{l, m};

0, если число α + i β не совпадает ни с одним корнем

характеристического уравнения (10.7); s =

k, если число α + i β совпадает с корнем кратности k этого характеристического уравнения.

В заключение отметим, что если правая часть системы (10.13) представляет собой сумму k вектор–функций вида (10.14), то частное решение этой системы находится с помощью принципа суперпозиции из § 9.

56

§11. Фазовая плоскость однородного линейного векторного уравнения размерности 2.

На фазовой плоскости Ox1x2 решения дифференциаль-

падают с фазовыми графиками дифференциального уравнения

x′′1 − σx′1 + δx1 = 0

(см. § 5). Так как собственные числа матриц

совпадают, то в случае A ≠ λI матрицы A и B оказываются подобными. Поэтому, на основании указанной выше связи между дифференциальной системой (11.2) и линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами, при A ≠ λI расположение траекторий дифференциальной системы (11.1) с точностью до линейного невырожденного преобразования описано в § 5.

57

Рассмотрим теперь оставшийся случай, т.е. когда диффе-

Общее решение дифференциальной системы (11.3) таково:

x1 = C1eλt, x2 = C2eλt.

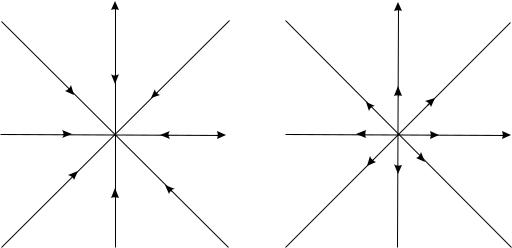
Если λ ≠ 0, то траектории дифференциальной системы (11.3) являются либо точкой покоя (при C1 = C2 = 0), либо лучами прямых, примыкающими к точке покоя. Такое расположение траекторий называют дикритическим узлом (рис. 11.1 а, б).

Рис. 11.1.

При λ = 0 каждая точка фазовой плоскости является точкой покоя дифференциальной системы (11.3).

58