Дифференциальные уравнения 2

Каждый график является эллипсом β2x2 +y2 = C12 +C22. Точку покоя с таким расположением соседних фазовых графиков называют центром (рис. 5.6).

Рассмотрим типы точек покоя без учета ограничения (5.9). Непосредственными вычислениями на основании вышеприведенного с учетом возможности замены t на −t получаем утверждение.

Теорема 5.2. Если a0 ≠ 0, то тип точки покоя O дифференциального уравнения (5.1) определяется видом корней характеристического уравнения (5.2), а именно:

1)λ1, λ2 R, λ1λ2 < 0 седло;

2)λ1, λ2 R, λ1λ2 > 0, λ1 ≠ λ2 бикритический узел;

3)λ1, λ2 R, λ1λ2 > 0, λ1 = λ2 монокритический узел;

4)λ1,2 = α + iβ, β ≠ 0, α ≠ 0 фокус;

5)λ1,2 = α + iβ, β ≠ 0, α = 0 центр.

Рассмотрим теперь случай a0 = λ1λ2 = 0. В этом случае дифференциальное уравнение (5.1) принимает вид

При любом ξ R функция x = x(t) = ξ, t R, является стационарным решением дифференциального уравнения (5.12). Поэтому вся ось y = 0 состоит из точек покоя, т.е. является прямой покоя.

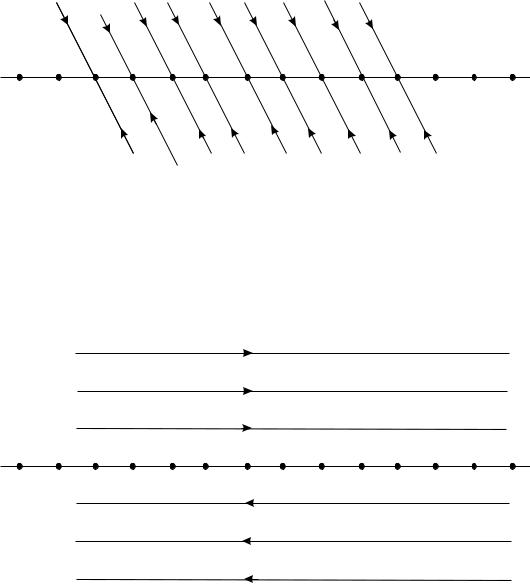
Если у характеристического уравнения (5.2) корни λ1 < λ2 = 0, то фазовые графики

x = C1 + C2eλ1t, y = λ1C2eλ1t,

расположены на лучах y = λ1(x − C1), y > 0, или y = λ1(x − C1), y < 0, и направлены к оси y = 0 (рис. 5.7).

Случай λ1 > λ2 > 0 сводится к предыдущему заменой t на

−t.

31

Y = 0

Рис. 5.7.

Если же корни λ1 = λ2 = 0, то a1 = 0 и дифференциальное уравнение (5.12) является уравнением x′′ = 0 с фазовыми графиками x = C1 + C2t, y = C2, расположенными на горизонтальных прямых и направленными в соответствии с рассмотренной нами схемой рис. 5.1 (см. рис. 5.8).

Y = 0

Рис. 5.8.

32

§ 6. Неоднородные линейные дифференциальные уравнения n–го порядка.

Рассмотрим неоднородное линейное дифференциальное уравнение n–го порядка

где ak(t), k = 0, n − 1, f(t) есть непрерывные на (a, b) функции. Дифференциальное уравнение (6.1) можно записать в виде

где L[x] есть линейный дифференциальный оператор из § 3.

Теорема 6.1. Общее решение неоднородного линейного дифференциального уравнения n–го порядка L[x] = f(t) представляет собой сумму некоторого его частного решения x (t) и общего решения x0(t) соответствующего однородного линейного дифференциального уравнения n–го порядка L[x] = 0.

Ранее мы показали, что если x1 и x2 есть два решения однородного линейного дифференциального уравнения n–го порядка L[x] = 0, то любая их линейная комбинация C1x1+C2x2 также есть решение этого уравнения. Кроме того, если x1 есть решение однородного линейного дифференциального уравнения n–го порядка L[x] = 0, а x2 есть решение неоднородного линейного дифференциального уравнения n–го порядка L[x] = f(t), то их сумма x1 + x2 есть решение последнего неоднородного дифференциального уравнения.

Покажем теперь, что если x1 есть решение дифференциального уравнения L[x] = f1(t), x2 есть решение дифференциального уравнения L[x] = f2(t), то сумма x1 +x2 есть решение дифференциального уравнения L[x] = f1(t) + f2(t). В самом деле, имеем, что L[x1 + x2] = L[x1] + L[x2] = f1(t) + f2(t).

33

Аналогичным образом доказываем, что если комплекснозначная функция вещественного переменного u(t)+i v(t) есть решение дифференциального уравнения L[x] = f1(t) + i f2(t), где f1(t) и f2(t) есть вещественные функции, то функции u(t) и v(t) являются решениями дифференциальных уравнений L[x] = f1(t) и L[x] = f2(t), соответственно.

Данные утверждения составляют основу принципа суперпозиции (наложения) решений неоднородных линейных дифференциальных уравнений. Он справедлив для любого конечного числа k частных решений.

Пусть известна фундаментальная система решений однородного линейного дифференциального уравнения n–го порядка L[x] = 0: – функции x1, . . . , xn. Тогда общее решение однородного линейного дифференциального уравнения есть

Метод вариации произвольных постоянных (метод Лагранжа) позволяет найти общее решение неоднородного линейного дифференциального уравнения L[x] = f(t), если известна фундаментальная система решений соответствующего однородного линейного дифференциального уравнения L[x] = 0. В соответствии с этим методом общее решение дифференциального уравнения L[x] = f(t) ищется в виде, сходном с функцией (6.3), считая, что коэффициенты C1, . . . , Cn являются уже не постоянными, а функциями от t, т.е. общее решение ищется в виде

где функции Ck(t) непрерывны на (a, b), k = 1, n. Нетрудно показать, что неизвестные функции Ck(t), k = 1, n, есть

34

Это есть неоднородная линейная система алгебраических уравнений относительно неизвестных функций Ck′ (t), k = 1, n, с определителем Вронского W [x1, . . . , xn], отличным от нуля, т.к. x1, . . . , xn есть фундаментальная система решений однородного линейного дифференциального уравнения L[x] = 0. Поэтому система (6.5) имеет единственное решение Ck′ (t) =

φk(t), k = 1, n, откуда

∫

Ck(t) = φk(t)dt + Ck, k = 1, n,

где Ck, k = 1, n, есть произвольные постоянные. При этом система (6.5) называется системой Лагранжа для неоднородного линейного дифференциального уравнения L[x] = f(t).

35

§ 7. Линейные неоднородные дифференциальные уравнения n–го порядка с постоянными коэффициентами.

Рассмотрим линейное неоднородное дифференциальное уравнение n–го порядка с постоянными коэффициентами ak

R, k = 0, n − 1:

где f(t) есть непрерывная на (a, b) функция. Его общее решение имеет вид

x = x + C1x1 + . . . + Cnxn,

где x есть частное решение дифференциального уравнения (7.1), а x1, . . . , xn, есть фундаментальная система решений однородного линейного дифференциального уравнения n–го порядка L[x] = 0 (ее мы научились находить в § 4). Поэтому для нахождения общего решения достаточно найти частное решение дифференциального уравнения (7.1). Для специального вида правых частей f(t) дифференциального уравнения (7.1) эта задача решается операциями дифференцирования и решения систем линейных алгебраических уравнений. Этот метод называется методом подбора частного решения или методом неопределенных коэффициентов. Правая часть дифференциального уравнения (7.1), для которой применим метод неопределенных коэффициентов, имеет вид

f(t) = eαt{Pm(t) cos βt + Ql(t) sin βt}, α R, β R, (7.2)

где Pm(t) и Ql(t) есть многочлены степеней m и l, соответственно.

Рассмотрим теперь частные случаи правых частей (7.2) и покажем, как к ним применяется метод неопределенных коэффициентов.

36

Случай 1. Правая часть дифференциального уравнения (7.1) имеет вид

где Am ≠ 0 и λ = 0 не является корнем характеристического уравнения (4.4). В этом случае будем искать частное решение x дифференциального уравнения (7.1) в виде многочлена той же m–й степени

с неопределенными пока коэффициентами Bk, k = 0, m. Для их отыскания подставляем функцию (7.4) в дифференциальное уравнение (7.1). После этого, сравнив коэффициенты при одинаковых степенях переменной t в правой и левой частях, получаем систему линейных алгебраических уравнений относительно коэффициентов Bk, k = 0, m.

Пример 7.1. Найдите общее решение дифференциального уравнения

Решение. Составляем характеристическое уравнение

λ2 − 8λ + 7 = 0,

находим его корни λ1 = 1, λ2 = 7, и получаем общее решение

x0 = C1et + C2e7t

соответствующего (дифференциальному уравнению (7.5)) однородного линейного дифференциального уравнения. Так как λ = 0 не является корнем характеристического уравнения, то частное решение x дифференциального уравнения (7.5)

ищем в виде

x = At2 + Bt + C.

37

Непосредственными вычислениями получаем, что x ′ = 2At + B, x ′′ = 2A.

Подставив x , x ′, x ′′, в дифференциальное уравнение (7.5), имеем, что

7At2 + (7B − 16A)t + (2A − 8B − 7C) = 3t2 + 7t + 8.

Приравнивая коэффициенты при одинаковых степенях t, по-

лучаем систему

7A = 3,

7B − 16A = 7,

2A − 8B + 7C = 8;

разрешая которую, имеем A = 3/7, B = 97/49, C = 1126/343. Поэтому общее решение дифференциального уравнения (7.5) имеет вид

Пусть теперь λ = 0 является корнем кратности k характеристического уравнения (4.4). Этот случай называется резонансным. В данном случае частное решение надо искать в

При этом множитель tk в (7.6) называется резонансным. Случай 2. Пусть теперь правая часть дифференциального

уравнения (7.1) имеет вид

где Am ≠ 0.

38

Если α не является корнем характеристического уравнения (4.4), то частное решение x дифференциального уравнения (7.1) с правой частью (7.7) ищется в виде

где Bk, k = 0, m, есть неизвестные пока коэффициенты. Если же α есть корень кратности k характеристического

уравнения (4.4) (резонансный случай), то частное решение x дифференциального уравнения (7.1) с правой частью (7.7) ищется в виде

Далее используется метод неопределенных коэффициентов. Пример 7.2. Найдите общее решение дифференциального

уравнения

Решение. В данном случае параметр α = 3. Характеристическое уравнение

λ2 − 2λ + 4 = 0

√

имеет пару комплексно сопряженных корней λ1,2 = 1 ± 3i. Поэтому общее решение соответствующего однородного линейного дифференциального уравнения имеет вид

Так как λ = 3 не является корнем характеристического уравнения, то частное решение x дифференциального уравнения (7.10) ищем в виде

x = (At + B)e3t.

Непосредственными вычислениями получаем, что

x ′ = e3t(3At + A + 3B), x ′′ = e3t(9At + 6A + 9B).

39

Подставив x , x′, x′′, в дифференциальное уравнение (7.10), после сокращения на e3t ≠ 0 имеем, что

Поэтому общее решение дифференциального уравнения (7.10) имеет вид

Случай 3. Правая часть дифференциального уравнения (7.1) имеет вид

Если α + iβ не является корнем характеристического уравнения (4.4), то частное решение x дифференциального уравнения (7.1) с правой частью (7.11) ищется в виде

x = eαt{Rs(t) cos βt + Ts(t) sin βt},

где Rs(t) и Ts(t) есть многочлены степени s = max{m, l} с неопределенными пока коэффициентами.

Если же α+iβ есть корень кратности k характеристического уравнения (4.4), то частное решение x дифференциального уравнения (7.1) с правой частью (7.11) ищется в виде

x = tkeαt{Rs(t) cos βt + Ts(t) sin βt},

где Rs(t) и Ts(t) есть многочлены степени s = max{m, l} с неопределенными коэффициентами.

Отметим, что если правая часть дифференциального уравнения (7.1) представляет собой сумму k функций вида (7.2), то частное решение дифференциального уравнения (7.1) находится с помощью принципа суперпозиции из § 6.

40