
- •А.В. Ряднов, в.В. Трубаев, т.В. Меренкова
- •Теория вероятностей
- •Учебное пособие
- •Москва - 2013
- •Оглавление
- •Глава I. Основные понятия и формулы теории вероятностей.
- •§1. Предмет теории вероятностей. Случайные события.
- •Задачи:
- •§4. Формула сложения вероятностей
- •§5. Аксиоматический подход к теории вероятностей
- •I. Аксиомы событий
- •II. Аксиомы вероятностей
- •§6. Классическая схема теории вероятностей
- •§7. Геометрические вероятности
- •§8. Условная вероятность. Независимость случайных событий.
- •§9. Формула полной вероятности. Формулы Байеса.
- •§10. Комбинаторика.
- •§11. Схема Бернулли
- •§12. Вероятности Pn(к) при больших значениях n. Приближённые формулы Лапласа и Пуассона.
- •Глава II. Случайные величины и их
- •Характеристики
- •§1. Случайная величина и её функция
- •Распределения
- •§2. Дискретные случайные величины
- •§3. Непрерывные случайные величины
- •§ 4. Функции от случайной величины.
- •§ 5. Системы случайных величин.
- •1. Двумерные дискретные случайные величины.
- •2. Непрерывные системы случайных величин.
- •§ 6. Независимые случайные величины.
- •§ 7. Математическое ожидание случайной величины.
- •1. Математическое ожидание дискретной случайной величины.
- •2. Математическое ожидание случайной величины, имеющей плотность вероятности.
- •§8. Дисперсия случайной величины.
- •§9. Корреляционный момент и корреляция случайных величин
- •Глава III. Закон больших чисел и центральная предельная теорема.
- •§ 1. Неравенство Чебышева.
- •§2. Закон больших чисел.
- •Полезное заключительное замечание о практическом значении изложенных выше теорем.
- •§ 3. Центральная предельная теорема Ляпунова и её следствия.
- •Задачи по теории вероятностей
- •Индивидуальные задания № 1 по Теории вероятностей
- •Задачи индивидуальных заданий № 1
- •Индивидуальные задания № 2 по Теории вероятностей
- •Задачи индивидуальных заданий № 2
- •Степени числа e
- •150048, Ярославль, Московский пр-т, д. 151,
§6. Классическая схема теории вероятностей
Рассмотрим частный случай, когда множество
Ω – пространство элементарных событий, является конечным множеством.
Пусть
элементы этого множества (элементарные
события) есть![]() .
Согласно схеме §5 любое событиеАесть подмножество в Ω, т.е.
.
Согласно схеме §5 любое событиеАесть подмножество в Ω, т.е.
![]()
Тогда,
поскольку
![]() - попарно несовместны, получаем
- попарно несовместны, получаем
![]() .
(1)
.
(1)
Значит,
чтобы знать вероятность события Анадо знать
![]() -
вероятности элементарных событий.
-
вероятности элементарных событий.
Рассмотрим
частный (классический) случай когда все
числа
![]() равны между собой:
равны между собой:
![]() .
Другими словами, все элементарные исходы
(события) опытаравновероятны.Тогда,
поскольку
.
Другими словами, все элементарные исходы
(события) опытаравновероятны.Тогда,
поскольку
![]() -достоверное
событие,
-достоверное
событие,
получаем
![]()
и
значит
![]() .
.
Значит из формулы (1) получаем: если событие Апредставляется в виде суммыкравновероятных элементарных событий, то его вероятность будет равна
![]() (к- слагаемых)
(к- слагаемых)
Или
![]() . (2)
. (2)
Формула (2) позволяет
решать многие задачи для нахождения
вероятностей. В соответствии со сказанным,
её применяют в тех случаях, когда для
данного опыта можно указать группу из
конечного числа событий
![]() со следующими свойствами:
со следующими свойствами:
1. В результате опыта каждый раз наступает одно и только одно из этих событий
2. Указанные события по условиям данного опыта равновероятны.
При выполнении этих условий вероятность события Авычисляется по формуле (2)
Обычно
события
![]() -
называют элементарными исходами
(случаями), а те элементарные исходы,
которые в сумме составляютА, называют
благоприятными исходами для событияА. В этой терминологии формула (2)
читается так: вероятность событияАравна отношению числа благоприятных
для событияАисходов к числу всех
(элементарных) исходов.
-
называют элементарными исходами
(случаями), а те элементарные исходы,
которые в сумме составляютА, называют
благоприятными исходами для событияА. В этой терминологии формула (2)
читается так: вероятность событияАравна отношению числа благоприятных
для событияАисходов к числу всех
(элементарных) исходов.
Пример 1. В урне находятся 10 шаров: 4 белых и 6 чёрных. Из урны наудачу извлекают шар. Какова вероятность, что он окажется чёрным ( событиеА)
Решение:
Представим себе, что шары снабжены
номерами 1,2,…,10. Обозначим через![]() следующее событие: извлечение шара с
номеромi . Тогда
события
следующее событие: извлечение шара с
номеромi . Тогда
события![]() будут элементарными исходами.
Действительно, при каждом осуществлении
опыта, наступает одно и только одно из
них, а слово « наудачу» в формулировке
задачи служит указанием на то, что все
события
будут элементарными исходами.
Действительно, при каждом осуществлении
опыта, наступает одно и только одно из
них, а слово « наудачу» в формулировке
задачи служит указанием на то, что все
события![]() равновероятны. Интересующему нас событиюАблагоприятны шесть исходов. Значит
в данном случаеn=10,k=6 и значит
равновероятны. Интересующему нас событиюАблагоприятны шесть исходов. Значит
в данном случаеn=10,k=6 и значит
![]() .
.
Замечание.При
решении этой задачи мы использовали
подробные (громоздкие) рассуждения. При
соответствующем навыке можно рассуждать
короче, например, так: из 10 возможных
случаев событиюА благоприятны 6,
следовательно,
![]() .
.
§7. Геометрические вероятности
В §5 была рассмотрена система аксиом теории вероятностей. Конкретные реализации этой системы, возникающих при решении практических задач, могут быть различными.
Так в классической схеме (§6) рассмотрена реализация, когда пространство Ω элементарных событий есть множество, состоящее из конечного числа nэлементов, причем вероятности этих элементов одинаковы. Рассмотрим ещё один наглядный пример реализации этой системы.
Пусть Ω есть некоторая область на прямой, плоскости или в пространстве. Условимся называть событиями всевозможные подмножества в Ω (которые можно измерить – т.е. найти их длину, площадь, объём). Каждому событию Апоставим в соответствии его вероятность по формуле
![]() , (1)
, (1)
где
![]() обозначает меру множестваА. Все
аксиомы – как для событий, так и для
вероятностей (см. §5) будут в этом
обозначает меру множестваА. Все
аксиомы – как для событий, так и для
вероятностей (см. §5) будут в этом
случае выполнены.
Особенностью этой
модели является её геометрический
характер: при этом существенно, что
вероятности Р(А) определяются не
конкретно формой множестваА и его
расположением в Ω , а единственно его
мерой
![]() .
.
К указанной выше геометрической схеме сводится довольно большой круг задач. В каждой из них элементарные события можно трактовать как случайный выбор точки в некоторой области Ω. При этом, условия задачи должны быть такими, чтобы все точки в Ω можно было считать «равноправными» (в смысле возможности их выбора).
Отметим одно следствие в этой (геометрической) схеме, не имеющего аналога в классической схеме.
Точка
ω в Ω является элементарным событием и
значит, исходя из формулы (1), получаем
![]() .
.
Итак, вероятности элементарных событий равны нулю. Тем не менее, эти события возможны: мы предполагаем, что можно попасть в любую точку ωобласти Ω.
Как можно истолковать такое явление?
В § 2 мы условились считать очень маловероятные события практически невозможными. Тем более следует считать практически невозможными события нулевой вероятности.
Итак, попадание в данную геометрическую точку ωнадо рассматривать, как событие практически невозможное, хотя теоретически оно и может произойти.
В качестве примера рассмотрим следующую «задачу о встрече».
Пример.Между 12-ью часами и часом дня должен произойти в случайный момент звонок квартирного телефона, причём вызывающий ждёт 10 минут. В течение этого же часа хозяин квартиры заходит домой в случайный момент и остается дома в течение 30 минут. Какова вероятность, что разговор состоится (событиеА).
Решение. Тот
факт, что звонок происходит в моменту,
а хозяин квартиры приходит в моментх,
можно изобразить точкой плоскости с
координатами (х;у); при этом будем
отсчитыватьх иув минутах от
12 часов. Тогда все возможные комбинации
вызова и прихода (элементарные исходы)
изобразятся точками квадрата Ω:![]()
![]() (см. рис.1). Поскольку, моменты звонка и
прихода случайны и не зависят друг от
друга, то все точки (элементарные исходы)
в квадрате можно считать равноправными
(в смысле возможности их выбора). Выясним
теперь, какие точки (х;у)
благоприятствуют событиюА(«разговор
состоялся»). Разговор может состояться
лишь в том случае, если момент звонка
не больше чем на тридцать минут раньше
момента прихода и не меньше чем на 10
минут позже прихода, т.е.
(см. рис.1). Поскольку, моменты звонка и
прихода случайны и не зависят друг от
друга, то все точки (элементарные исходы)
в квадрате можно считать равноправными
(в смысле возможности их выбора). Выясним
теперь, какие точки (х;у)
благоприятствуют событиюА(«разговор
состоялся»). Разговор может состояться
лишь в том случае, если момент звонка
не больше чем на тридцать минут раньше
момента прихода и не меньше чем на 10
минут позже прихода, т.е.![]() .
.
Итак, область G квадрата, благоприятствующая А, состоит из точек (х;у), координаты которых удовлетворяют
неравенствам
![]() ,
,![]() ,
то есть из точек, лежащих между прямыми
,
то есть из точек, лежащих между прямыми![]() (см. рис 1).
(см. рис 1).
П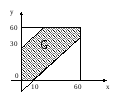 лощадь
квадрата равна 3600; вычитая площади двух
угловых треугольников, находим, что,
площадь области G равна
лощадь
квадрата равна 3600; вычитая площади двух
угловых треугольников, находим, что,
площадь области G равна![]()
Рис.1
Отсюда получаем искомую вероятность
![]() .
.
