§8. Дисперсия случайной величины.

Во многих случаях возникает необходимость ввести ещё одну числовую характеристику для измерения степени рассеивания, разброса значений, принимаемых случайной величинойξ, вокруг её математического ожидания.

Определение.Дисперсией случайной величиныξназывается число.

D ξ =M(ξ-M ξ)². (1)

Другими словами, дисперсия есть математическое ожидание квадрата отклонения значений случайной величины от её среднего значения.

Число

(2)

называется средним квадратичнымотклонением

величины ξ.

Если дисперсия характеризует средний размер квадрата отклонения ξoтMξ, то числоможно рассматривать как некоторую среднюю характеристику самого отклонения, точнее, величины |ξ-Mξ|.

Из определения (1) вытекают следующие два свойства дисперсии.

1. Дисперсия постоянной величины равна нулю. Это вполне соответствует наглядному смыслу дисперсии, как «меры разброса».

Действительно, если

ξ=С,тоMξ=Cи, значит Dξ=M(C-C)²=M0=0.

2. При умножении случайной величины ξна постоянное число С её дисперсия умножается наC²

D(Cξ)=C²Dξ. (3)

Действительно

D(Cξ)=M(C

=M(C.

3. Имеет место, следующая формула для вычисления дисперсии:

. (4)

Доказательствоэтой формулы следует из свойств математического ожидания. Мы имеем:

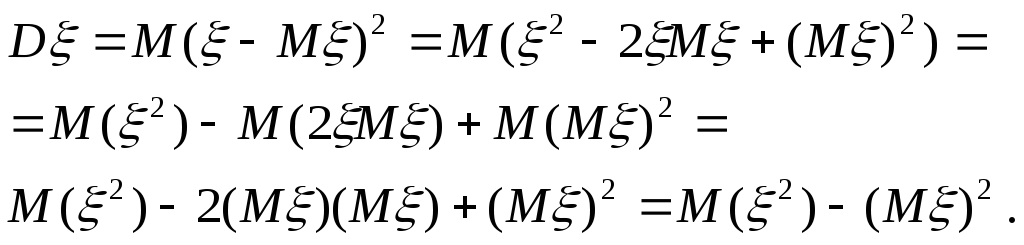
4. Если величины ξ₁иξ₂независимы, то дисперсия их суммы равна сумме их дисперсий:

. (5)

Доказательство.Для доказательства используем свойства математического ожидания. ПустьMξ₁=m₁,Mξ₂=m₂, тогда.

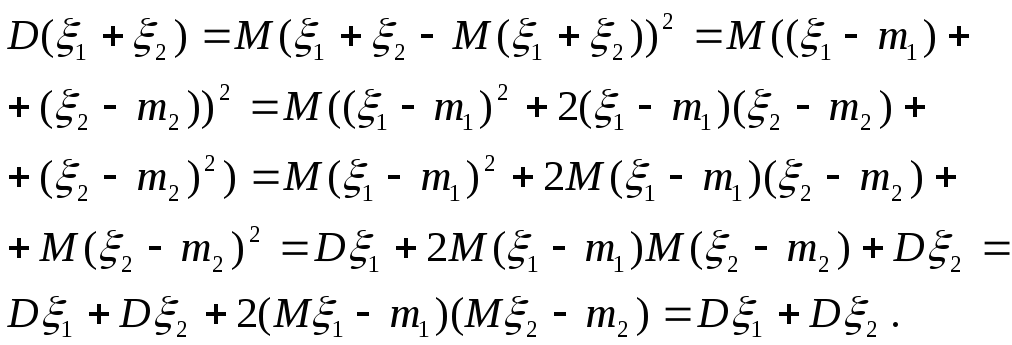
Формула (5) доказана.

Так как дисперсия случайной величины есть по определению математическое ожидание величины (ξ –m)², гдеm=Mξ ,то для вычисления дисперсии можно воспользоваться формулами, полученными в §7 гл.II.

Так, если ξесть ДСВ с законом распределения

x1	x2	...
p1	p2	...

то будем иметь:

. (7)

Если ξнепрерывна случайная величина с плотностью распределенияp(x), тогда получим:

Dξ=. (8)

Если использовать формулу (4) для вычисления дисперсии, то можно получить другие формулы, а именно:

, (9)

если величина ξдискретна, и

Dξ=, (10)

если ξраспределена с плотностьюp(x).

Пример 1.Пусть величинаξравномерно распределена на отрезке [a,b]. Воспользовавшись формулой (10) получим:

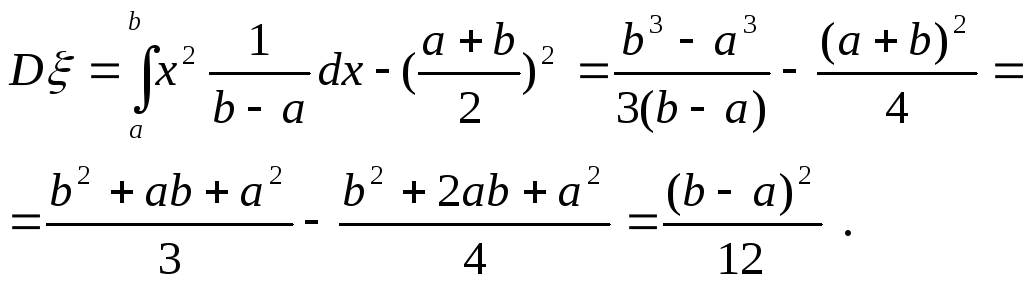
Можно показать, что дисперсия случайной величины , распределенной по нормальному закону с плотностью

p(x) =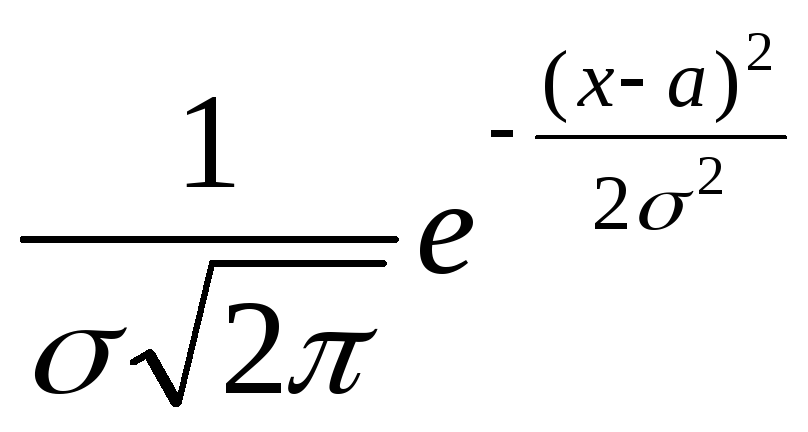, (11)

равна σ².

Тем самым выясняется смысл параметра σ, входящего в выражение плотности (11) для нормального закона; σ ecть среднее квадратичное отклонение величиныξ.

Пример 2.Найти дисперсию случайной величиныξ, распределенной по биномиальному закону.

Решение.Воспользовавшись представлениемξв виде

ξ=ξ₁+ξ₂+…+ξ_n(см. пример 2 §7 гл.II) и применяя формулу сложения дисперсий для независимых величин, получим

Dξ=Dξ₁+Dξ₂+…+ Dξ_n.

Дисперсия любой из величин ξ_i (i=1,2,…,n) подсчитывается непосредственно:

Dξ_i=M(ξ_i)²- (Mξ_i)²=0²·q+1²p-p²=p(1-p)=pq.

Окончательно получаем

Dξ=npq, гдеq=1– p.