
- •А.В. Ряднов, в.В. Трубаев, т.В. Меренкова
- •Теория вероятностей
- •Учебное пособие
- •Москва - 2013
- •Оглавление
- •Глава I. Основные понятия и формулы теории вероятностей.
- •§1. Предмет теории вероятностей. Случайные события.
- •Задачи:
- •§4. Формула сложения вероятностей
- •§5. Аксиоматический подход к теории вероятностей
- •I. Аксиомы событий
- •II. Аксиомы вероятностей
- •§6. Классическая схема теории вероятностей
- •§7. Геометрические вероятности
- •§8. Условная вероятность. Независимость случайных событий.
- •§9. Формула полной вероятности. Формулы Байеса.
- •§10. Комбинаторика.
- •§11. Схема Бернулли
- •§12. Вероятности Pn(к) при больших значениях n. Приближённые формулы Лапласа и Пуассона.
- •Глава II. Случайные величины и их
- •Характеристики
- •§1. Случайная величина и её функция
- •Распределения
- •§2. Дискретные случайные величины
- •§3. Непрерывные случайные величины
- •§ 4. Функции от случайной величины.
- •§ 5. Системы случайных величин.
- •1. Двумерные дискретные случайные величины.
- •2. Непрерывные системы случайных величин.
- •§ 6. Независимые случайные величины.
- •§ 7. Математическое ожидание случайной величины.
- •1. Математическое ожидание дискретной случайной величины.
- •2. Математическое ожидание случайной величины, имеющей плотность вероятности.
- •§8. Дисперсия случайной величины.
- •§9. Корреляционный момент и корреляция случайных величин
- •Глава III. Закон больших чисел и центральная предельная теорема.
- •§ 1. Неравенство Чебышева.
- •§2. Закон больших чисел.
- •Полезное заключительное замечание о практическом значении изложенных выше теорем.
- •§ 3. Центральная предельная теорема Ляпунова и её следствия.
- •Задачи по теории вероятностей
- •Индивидуальные задания № 1 по Теории вероятностей
- •Задачи индивидуальных заданий № 1
- •Индивидуальные задания № 2 по Теории вероятностей
- •Задачи индивидуальных заданий № 2
- •Степени числа e
- •150048, Ярославль, Московский пр-т, д. 151,
1. Двумерные дискретные случайные величины.
Пусть
на вероятностном пространстве (Ω,S,P)
заданы дискретные случайные величины![]() ,
тогда двумерную случайную величину
,
тогда двумерную случайную величину![]() будем называть дискретной.
будем называть дискретной.
Пусть
![]() - все возможные значения
- все возможные значения![]() ,
,![]() -
все возможные значения
-
все возможные значения![]() .
Как мы уже знаем, с помощью вероятностей
.
Как мы уже знаем, с помощью вероятностей![]() и
и![]() определяются законы распределения
случайных величинξиη. Ясно,
что возможные значения двумерной
случайной величины
определяются законы распределения
случайных величинξиη. Ясно,
что возможные значения двумерной
случайной величины![]() содержатся
среди пар
содержатся
среди пар![]() точек на плоскости. Рассмотрим вероятности
точек на плоскости. Рассмотрим вероятности
![]() Тогда с помощью
этих вероятностей
Тогда с помощью
этих вероятностей
![]() можно найти вероятность
можно найти вероятность![]() ,
гдеВ- произвольное множество точек
плоскости, а именно:
,
гдеВ- произвольное множество точек
плоскости, а именно:
![]() . (3)
. (3)
Отсюда вытекает, что исчерпывающей характеристикой (законом распределения) двумерной дискретной системы может служить таблица
|
|
|
|
… |
|
… |
|
|
|
|
… |
|
… |
|
|
|
|
… |
|
… |
|
… |
… |
… |
… |
… |
… |
|
|
|
|
… |
|
… |
|
… |
… |
… |
… |
… |
… |
Эта таблица называется совместным законом распределения случайных величин ξиη.
Из
определения
![]() следует, что
следует, что
![]() и
и
![]() .
(4)
.
(4)
Любая таблица такого вида задает некоторый закон совместного распределения пары случайных величин, который и называется двумерным законом распределения.
Из двумерного закона распределения можно получить одномерные законы распределения для ξ и для η:
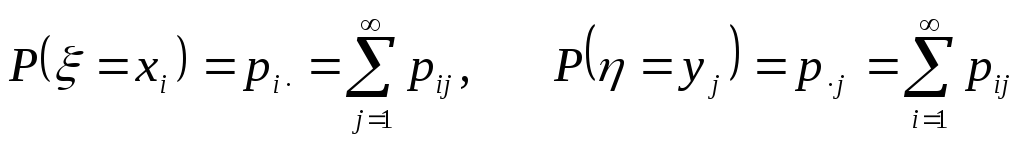 ,
(5)
,
(5)
поскольку
событие
![]() является суммой несовместных событий
является суммой несовместных событий![]() ,
а событие
,
а событие![]() суммой несовместных событий
суммой несовместных событий![]() .
.
Законы распределения (5) иногда называются маргинальными законами первоначального двумерного распределения.
Пример.В урне
лежат четыре шара , 2 белых, 1 чёрный и 1
синий. Из урны наугад извлекают два шара
(без возвращения) Пустьξ- число
чёрных, аη- число синих шаров в
выборке. Составить для системы![]() закон
распределения.
закон
распределения.
Решение.В
данном случае возможные значения для![]() иηесть 0 и 1 . Имеем:
иηесть 0 и 1 . Имеем:
![]() (событие (
(событие (![]() )
наступает только при одном из
)
наступает только при одном из![]() исходов опыта),
исходов опыта),![]() (событие (
(событие (![]() )
наступает только при двух исходах),
)
наступает только при двух исходах),
![]()
Искомый закон распределения задаётся следующей таблицей:
|
|
0 |
1 |
|
0 |
|
|
|
1 |
|
|
2. Непрерывные системы случайных величин.
Так
же как и раньше мы определим двумерную
непрерывную случайную величину
![]() как такую случайную величину, функция
распределения которой
как такую случайную величину, функция
распределения которой![]() непрерывна.
непрерывна.
С
помощью функции
![]() можно найти вероятность любого события
вида
можно найти вероятность любого события
вида
![]() ,
(6)
,
(6)
т.е.
вероятность попадания точки с координатами
![]() в прямоугольникQвида
в прямоугольникQвида
![]() (Рис.1)
(Рис.1)

Для
этого применим к событиям
![]() и
и![]() формулу сложения вероятностей:
формулу сложения вероятностей:
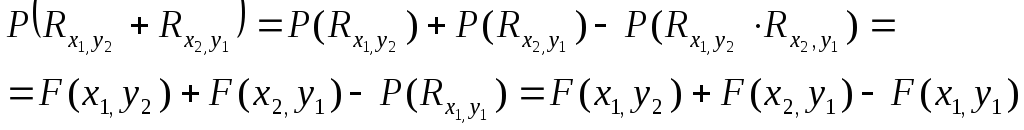 Если
теперь учесть, что события
Если
теперь учесть, что события
![]() и (6) несовместны и в сумме составляют
событие
и (6) несовместны и в сумме составляют
событие![]() ,
то будем иметь:
,
то будем иметь:
![]() что и решает
поставленную задачу.
что и решает
поставленную задачу.
Перечислим ряд
свойств функции
![]() .
Их доказательство проводится так же,
как и в случае одной случайной величины
.
.
Их доказательство проводится так же,
как и в случае одной случайной величины
.
1. F(x2,y2)+F(x1,y1)-F(x1,y2)-F(x2,y1)≥0, еслих1≤х2, у1≤у2это следует из (7)
2. F(x, y)является неубывающей функцией по каждому из аргументов.
3. F(x, y)непрерывна слева по каждому из аргументов.
4. F(x, y)удовлетворяет соотношениям:
F (+∞,
+∞ ) =![]() F(х, y
)=1,
F(х, y
)=1,
![]()
Свойства 1-4, как можно показать, являются характеристическимисвойствами функции распределения. Это значит, что любая функцияF(х, у), удовлетворяющая свойствам 1-4, является двумерной функцией распределения для некоторой системы случайных величин (ξ ,η).
Рассмотрим наиболее важный класс систем (ξ,η) с непрерывным распределением, для которых существует плотность вероятности.
Определение. Двумерная случайная величина (ξ,η) с функцией распределенияF(x,y)имеет плотность вероятности, если существует неотрицательная функция
p(x, y) такая, что
F(x,
y)=![]() .
(8)
.
(8)
Функция p(х,у)называется двумерной плотностью распределения (или плотностью вероятности) системы (ξ, η).
Из определения плотности p(x, y) следуют её свойства.
p(х,y)≥0,![]() .
(9)
.
(9)
Функция p(х,у), удовлетворяющая (9), может быть плотностью некоторого распределения с функцией распределения, заданной формулой (8).
Из формулы (8) следует, что
p(х,у)=![]() .
(10)
.
(10)
Заметим, что в
случае непрерывного распределения,
вероятность события ( (ξ,η)
![]() Г), где Г-кривая на плоскости, равна нулю.
Г), где Г-кривая на плоскости, равна нулю.
Из
определения
![]() также следует, что
также следует, что
Fξ(x)=![]() .
.
В случае существования плотности формула (7) преобретает наглядный вид:
P(x1≤ξ≤x2,
y1≤η≤y2)=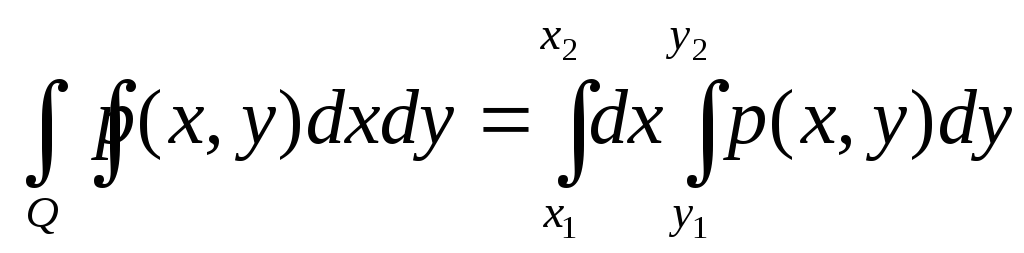 ,
(11)
,
(11)
где Q- прямоугольник (см. рис.1).
Из формулы сложения вероятностей и определения двойного интеграла, отсюда следует, что вероятность попадания точки с координатами (ξ,η) в заданную (измеримую) область произвольной формы Gбудет равна
P((![]() )
)![]() G)=
G)=![]() . (12)
. (12)
Примером многомерной плотности служит плотность p(x,y)равномерного распределения на областиGконечной площадиμ(G) в плоскости, задаваемая равенством
p(x,y)=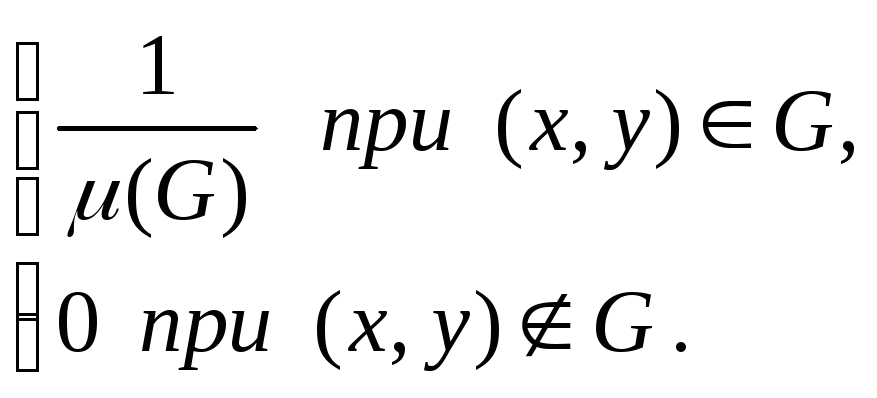
Если Вкакая то область на плоскости, то вероятность
P((ξ,η)![]() B)) в этом случае
определяется отношением площадейB∩GиG:
B)) в этом случае
определяется отношением площадейB∩GиG:
. (13)
По этой формуле вычисляются, так называемые, геометрические вероятности(см. §7 гл.1).
