§ 6. Независимые случайные величины.

При рассмотрении системы двух случайных величин (ξ,η) надо иметь в виду, что свойства системы не всегда исчерпываются свойствами самих величинξ,η. Дело в том, что между величинамиξ,η, может существовать зависимость и без учёта этой зависимости нельзя построить закон распределения системы (ξ,η). В этом параграфе мы рассмотрим случай независимости случайных величин.

Определение.Случайные величиныξ₁,ξ₂,…ξ_nназываютсянезависимыми, если для любых борелевских множествB_i выполняется равенство:(1)

Другими словами события:

независимы (см.§8 гл.1 определение 4). Если взять B_i = ),то из (1), в случае независимостиξ₁,…ξ_n, будет следовать равенство для многомерной функции распределения:

=(2)

Если распределение имеет плотность , то равенство (2) эквивалентно равенству (см (10) §5 гл.II)

=. (3)

Если случайные величины ξ₁,…ξ_n дискретны, то за определение независимости в этом случае можно принять равенство (см (1):

, (4)

где ,…, – возможные значения случайных величинξ₁,…,ξ_n, соответственно.

Можно показать, что если есть непрерывные (или кусочно непрерывные) функции, то случайные величинытакже будут независимы.

Формула композиции.Пусть дана система двух случайных величин (ξ,η) с плотностью=p(x,y).Найдем закон распределения суммыξ+η.

Функция распределения суммы ξ+ηравна следующему интегралу:

, где G=((x,y):x+y<z) есть полуплоскость с граничной прямойx+y=z(см рис.1 областьGзаштрихована).

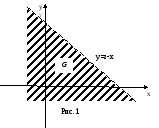
Вычислим этот интеграл как повторный

Сделав замену переменных , получим

.

Итак, мы получили

.

Поскольку , то значит плотность распределенияξ+ηвыражается через плотностьP(x,y)двумерного распределения (ξ,η)формулой

Рассмотрим случай, когда величины ξиηнезависимы. Тогда в этом случаеP_ξ,η(x,y)=P_ξ(x)P_η(y) и формула (5) принимает вид

В этом случае из формулы (6) следует, что

Формулы (6), (7) носят название формул композицииисвёртки. С помощью их мы выражаем плотностьP_ξ+η(z)и функцию распределенияF_ξ+η(z)суммы независимых случайных величин через плотности и функции распределения слагаемых.

Пример 1.Пустьξиηнезависимы,F_ξ(х)функция распределенияξ, аηимеет плотность (равномерно распределена на [a,b])

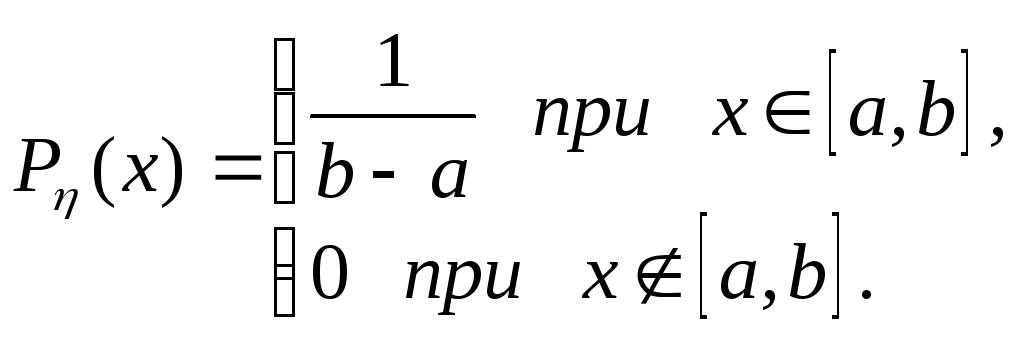
Применяя формулу композиции имеем.

,

делая замену в интеграле , получаем

.

Поскольку , то мы получаем формулу для плотности:

Пример 2.Рассмотрим частный случай примера 1, когда величиныξиηравномерно распределены на отрезке [0,1]

,

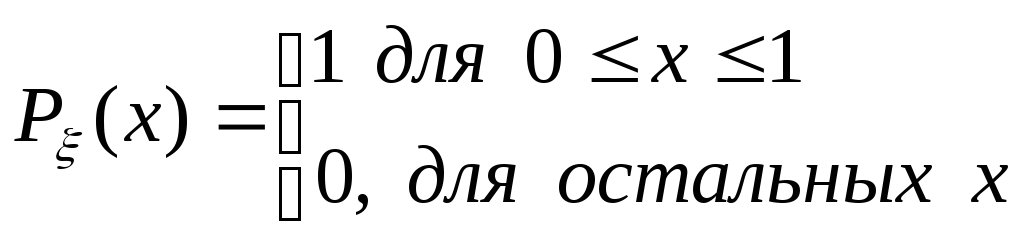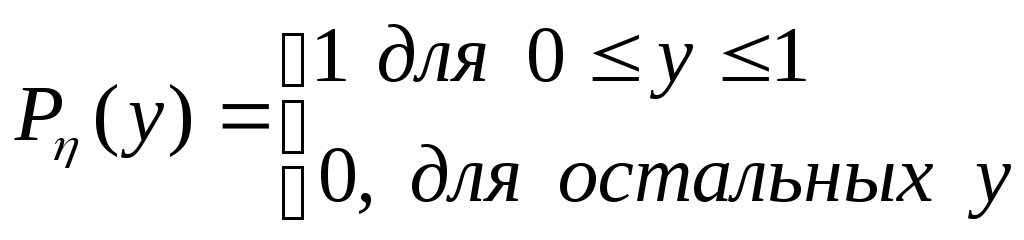
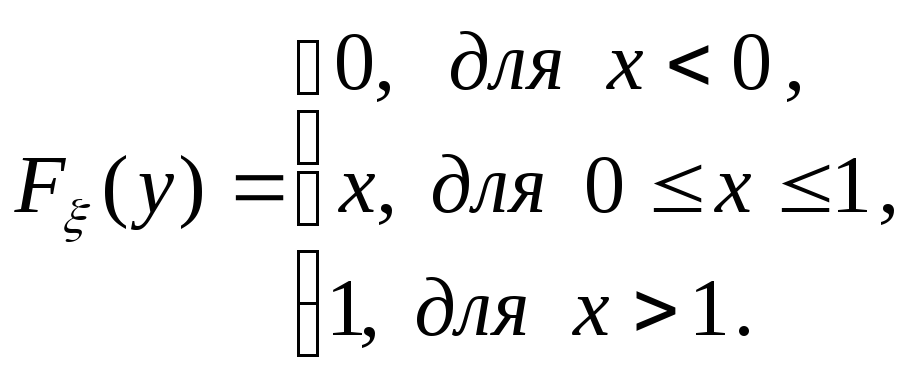
Тогда из формулы (8) получаем

График функции P_ξ+η(z) показан на рисунке 2.

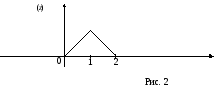
z

Замечание. Из формулы (5) можно также установить, что сумма независимых случайных величин, распределенных по нормальному закону, сама имеет нормальное распределение.

§ 7. Математическое ожидание случайной величины.

Согласно изложенному выше, исчерпывающей характеристикой случайной величины является её закон распределения (функция распределения). Но далеко не в каждой задаче нужно знать весь закон распределения. В ряде случаев можно обойтись одним или несколькими числами, отражающими наиболее важные особенности закона распределения, например числом, имеющим смысл среднего значенияслучайной величины, или же числом, характеризующим средний размер отклонения случайной величины от своего среднего значения и т.д. Такого рода числа называютчисловыми характеристикамислучайной величины (или соответствующего закона распределения). Их роль в теории вероятностей очень велика; многие задачи удаётся решить до конца, оставляя в стороне законы распределения и оперируя только числовыми характеристиками. Наиболее важные числовые характеристики:математическое ожиданиеидисперсиюслучайной величины, мы рассмотрим в этом и следующем параграфах.