§12. Вероятности Pn(к) при больших значениях n. Приближённые формулы Лапласа и Пуассона.

В приложениях часто возникает необходимость в вычислении вероятностей Р_n(к)для весьма больших значенийnиk. Рассмотрим, например, такую задачу.

Задача.На некотором предприятии вероятность брака, равна 0,02. Обследуются 500 изделий готовой продукции. Найти вероятность того, что среди них окажется ровно 10 бракованных.

Рассматривая обследование каждого изделия как отдельный опыт, можно сказать, что производиться 500 независимых опытов, причем в каждом их них событие А(изделие оказалось бракованным) наступает с вероятностью 0,02, тогда по формуле Бернулли получаем

.

Непосредственный подсчет этого выражения представляется сложным. Ещё большую трудность пришлось бы испытать, если бы мы искали вероятность того, что число бракованных изделий среди 500 окажется в пределах, скажем, от 10 до 20. В этом случае потребовалось бы вычислить сумму , что является более сложным делом.

Задачи подобного рода встречаются в приложениях весьма часто. Поэтому возникает необходимость в отыскании приближённых формул для вероятностей Р_n(к), а также для сумм вида

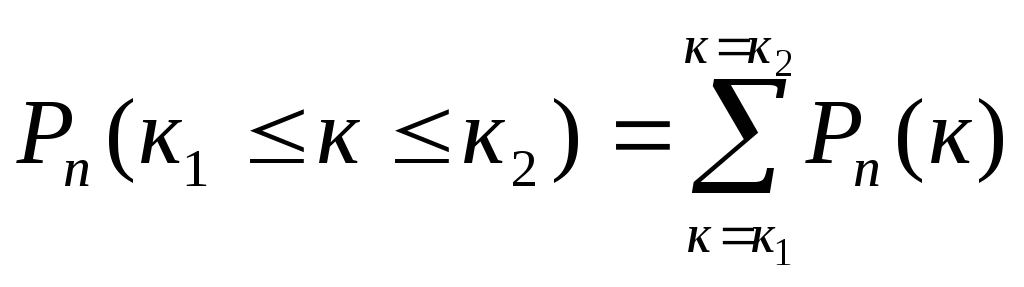(1)

при больших n.

1. Приближённые формулы Лапласа.Их используют при большихn(порядка сотен или тысяч), вероятностейpилиqне слишком близким к 0 или 1 (порядка сотых долей). Обычно условием применения этих приближений является условиеnpq>9.

а) Локальная приближённая формула Лапласа. При большихnсправедливо равенство.

, (2)

где , аφ(х) обозначает следующую функцию:.

Заметим, что функция φ(х)табулирована, т.е. для нее составлена таблица её значений.

Вторая приближённая формула Лапласа даёт приближённые значения для величины -вероятности того, что число наступлений событияАвnопытах (число «успехов») окажется заключенным между заданными границамик₁ ик₂.

б) Интегральная приближённая формула Лапласа. При большихnсправедливо приближённое равенство

, (3)

где Φ(х)обозначает следующую функцию

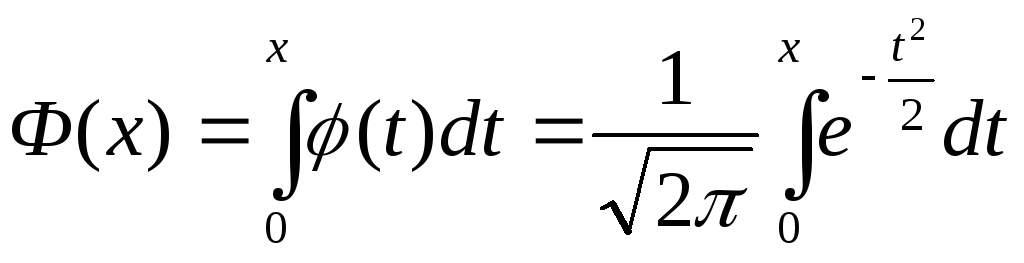. (4)

Функция Φ(х)обладает следующими полезными для вычисления свойствами:

1. Φ(х)– нечётная функция: ,

2. при возрастании хот 0 до ∞ функцияΦ(х)растет от 0

до 0,5, причем уже при х= 5 значение функцииΦ(х)

отличается от 0,5 меньше чем на (т.е. прифункцияФ(x) практически равна 0,5 ).

Пример 1.Монету бросают 100 раз. Какова вероятность того, что герб выпадет ровно 50 раз?

Решение. Имеем:npq= 100··= 25>9. Воспользовавшись приближённой формулой (2), получим.. Из таблицы для функцииφ(x)найдем, что φ(0) = 0,3989…. Отсюда получаем.

Пример 2. Доведём до конца решение задачи, приведённой в начале этого параграфа. В ней требовалось найти, а также вероятностьP₅₀₀(10≤к ≤20).

Решение. В данном случаеnpq= 500·0,02·0,98=9,8. Воспользовавшись приближёнными формулами (2) и (3), получим:,

Замечание.Если мы осуществляем опытnраз иk- число наступлений событияАпри этом, то, вообще говоря, дробь-относительная частота наступления события

А– будет близка кр(вероятности событияА). Однако сколь тесной окажется эта близость, предугадать невозможно.

Интегральная теорема Лапласа позволяет оценить вероятность неравенства при достаточно большихnи значенияхрне слишком близких к 0 или 1, т.е. определить вероятностьтого, что отклонение частотыслучайного события от его вероятностирпо абсолютной величине не превосходит некоторого. Имеем

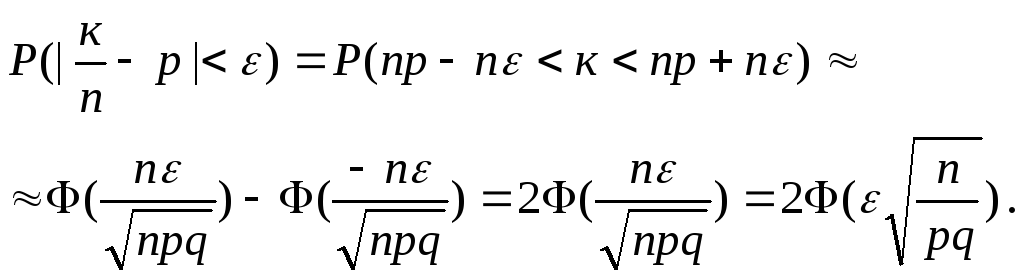
Таким образом, получаем

(5)

Вероятность в этом случае называютнадёжностью оценки, а сама оценкадоверительной оценкойчастотыс надёжностью .

На практике надёжность оценки задаётся заранее. Тогда по заданной надёжностиможно найти соответствующее значениеиз уравненияс помощью таблиц функции Лапласа. В этом случае доверительная оценка с заданной надёжностью примет вид

, где (6)

(найдено из уравнениясмотри (5)).

Это неравенство означает, что частота с заданной надёжностьюдолжна лежать в интервале (p-ε, p+ε). Этот интервал называетсядоверительным интервалом.

Пример 3. Какова вероятностьтого, что в 10 000 независимых испытаниях частота наступления события будет иметь отклонение от его вероятностиp=0,36 не более чем на 0,01?

Решение. Искомая вероятность вычисляется по формуле (5). Здесьn=10000, р=0,36,q=0,64,ε=0,01, тогда

.

Отсюда получаем:

.

Пример 4. Вероятность приёма некоторого сигнала равнар= 0,72. Определить, какое должно быть общее количество принятых сигналов, чтобы частота приёма этого сигнала отличалась от вероятности его приёма не более чем наε=0,1 с надежностью= 0,95.

Решение: Воспользуемся формулой(5).

У нас р=0,72,q=0,28,По таблице для

находим, что Значитt=1,96. Тогда из выражения находимn: ,

откуда n≈76,8. Так какnдолжно быть целым, то общее количество принятых сигналов равно 77.

2. Приближённые формулы Пуассона. Точность приближённых формул Лапласа понижается по мере приближения одного из чиселрилиqк нулю, поэтому, в этом случае используют приближённые формулы Пуассона. При большихn(порядка тысяч, десятков тысяч и больше) и малыхр(порядка тысячных долей и меньше) справедливы приближённые равенства. Обычно условием применения этих приближений является условиеnpq<9.

, (7).

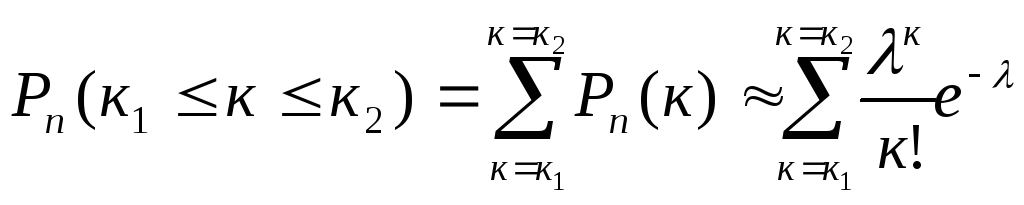, (8)

где λ =np.

Особенностью формул (7) и (8) является то, что для того, чтобы найти вероятность того или иного числа успехов, вовсе не требуется знать nир. Всё определяется числом λ=np, которое является (см. §11)средним числом успехов.

Для выражения , рассматриваемого как функция двух переменных киλ, составлены таблицы значений.

Пример 5. Прядильщица обслуживает 1000 веретён. Вероятность обрыва нити на одном веретене в течение одной минуты равна 0,004. Найти вероятность того, что в течение одной минуты обрыв произойдет в пяти веретенах.

Решение.Формула Бернулли приведёт к громоздким вычислениям, поэтому воспользуемся формулой Пуассона (7). Здеськ = 5,р=0.004,n= 1000, тогда λ =np= 4.

Отсюда: .

Пример 6. Книга в 1000 страниц имеет 100 опечаток. Какова вероятность того, что на случайно выбранной странице будет не менее четырёх опечаток (событиеВ).

Решение:Среднее количество опечаток на одну страницу есть. В данном случае следует применить формулу Пуассона. Тогда вероятностьp_к иметькопечаток на одной странице будет равна.

Сумма р =p₀+p₁+p₂+p₃есть вероятность того, что на странице окажется не более трёх опечаток. Пользуясь таблицами (или калькулятором) получаемр= 0,999996 (в данном случае мы пользовались калькулятором, таблицы дадутр=0,9048+0,0905+0,0045+0,0002=1). Вероятность того, что на случайно выбранной странице будет не менее четырёх опечаток, равна 1-р=1-0,999996=0,0000004 (таблицы дадут 1-р=1-1=0). Отсюда можно сделать вывод, что событиеВпрактически невозможно.