§2. Дискретные случайные величины

Определение 1. Если случайная величина принимает конечное или счётное число значений, то случайная величина называется дискретной (обозначение ДСВ).

Закон распределениядискретной случайной величиныξопределяется значениямикоторые принимаетξи вероятностямиэтих значений. Закон распределения можно определить с помощью таблицы, верхний ряд которой состоит из различных чиселх_i , а числа нижнего ряда из чисел p_i

		…		…
		…		…

Таблица (а значит закон распределения) служит исчерпывающей характеристикой ДСВ, поскольку по этой таблице однозначно восстанавливается функция распределения F(x)ДСВξ.

Остается ещё добавить, что

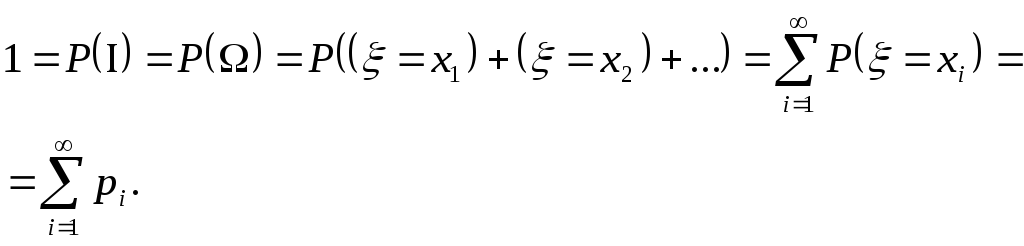
Итак

(1)

Выясним, какой вид имеет функция распределения ДСВ.

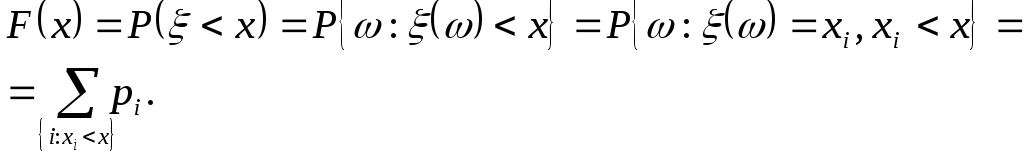Итак

. (2)

На рисунке 1 изображен график этой функции для частного случая, когда ξпринимает только три значения

Если .

Если .

Если .

График представляет собой ступенчатую ломаную со скачками в точках . Величины скачков равны соответственно. Аналогичная ступенчатая ломаная будет получаться для любой ДСВξ.

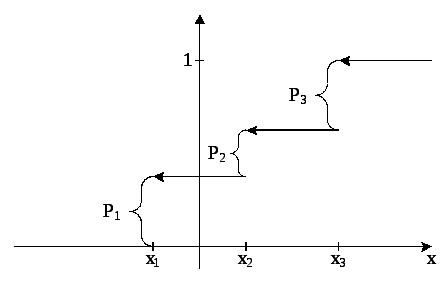Рис. 1

Примеры законов распределения ДСВ:

1. Биномиальный закондля числа успеховξприnнезависимых испытаниях в схеме Бернулли:

.

2. Гипергеометрическое распределение числа белых шаровξв выборке без возвращения объемаnиз урны, содержащейmбелых иN- mчерных шаров (см.§1)

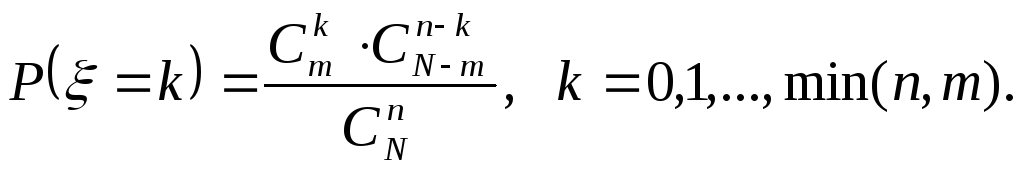
3. Равномерное распределениена множестве

4. Пуассоновское распределениечисла вызововξна телефонную станцию, поступающих за единицу времени, если λ есть среднее число вызовов, поступающих за единицу времени

.

5. Геометрическое распределение.Производится ряд независимых опытов, в каждом из которых с одной и той же вероятностьюpнаступает событиеА. Опыты продолжаются до первого появления событияА, после чего прекращаются. Случайная величинаξ– число произведённых опытов, распределена по геометрическому закону

.

§3. Непрерывные случайные величины

Определение 1. Случайная величинаξназывается непрерывной случайной величиной (обозначение НСВ), если её функция распределенияF(x)непрерывна при всех значенияхx.

Принимая во внимание формулу (4) из §1 получаем, что для НСВ вероятность каждого её отдельного значения равна нулю.

Значение НСВ уже могут заполнять конечный или бесконечный промежуток (α,β) числовой оси.

Один из способов построения НСВ заключается в следующем. Рассмотрим неотрицательную интегрируемую функцию P(x), определённую на всей числовой оси и удовлетворяющую условию:

. (1)

Положим

. (2)

Определённая таким образом функция F(x)обладает всеми характеристическими свойствами функции распределения (см.§1), к тому же она будет непрерывной. Значит (см.теорема 3.§1) функцияF(x)является функцией распределения некоторой случайной величиныξ.

Чаще всего рассматривают НСВ, обладающие плотностью.

Определение 2. Мы будим говорить, что случайная величинаξраспределена с некоторой плотностью, если существует неотрицательная функцияP_ξ(x),Такая, что для всехх справедливо равенство

, (3)

где F_ξ(x) – функция распределения случайной величины ξ.

Функция P_ξ(x)называетсяплотностью распределенияилиплотностью вероятностислучайной величины ξ.

В виду выше сказанного ясно, что случайная величина, имеющая плотность вероятности, непрерывна.

Обратное верно не всегда: существуют НСВ, для которых не существует плотности.

Ясно так же, что плотность вероятности должна удовлетворять условию (1), т.е.

. (4)

Это следует из соотношения .

Из определения плотности распределения следует:

1. в точках непрерывности,

2.

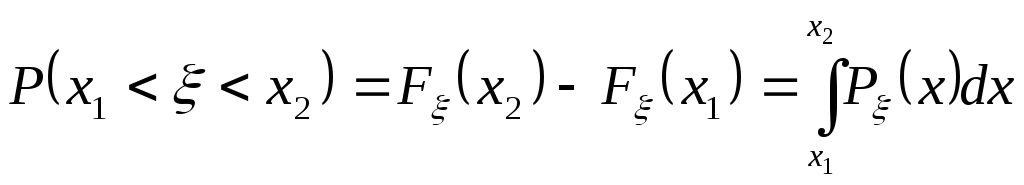
для любых .

Поясним смысл названия «плотность вероятности».

Согласно выше сказанному

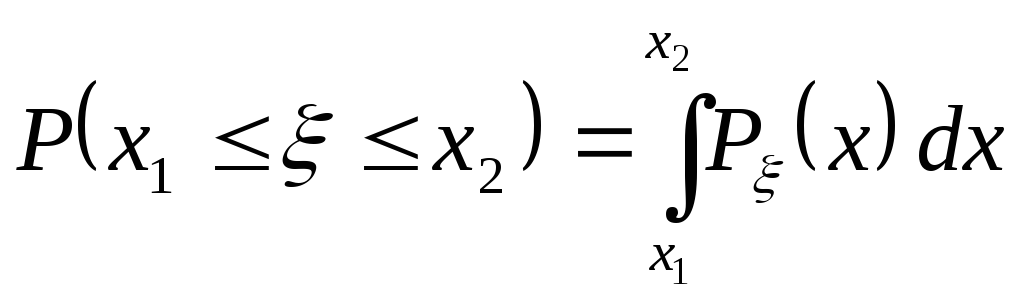. (5)

По теореме о среднем интеграл, стоящей в правой части (5) равен , где, и значит

. (6)

Левая часть формулы (6) представляет собой среднюю вероятность попадания значений случайной величины ξ на отрезке .

Теперь если мы будем стягивать отрезокк некоторой точкеи предположим, чтонепрерывна в этой точке, то мы получим:

.

Поскольку отношение, стоящее под знаком предела, есть своего рода «вероятность на единицу длины отрезка », то предел этого отношенияестественно рассматривать какплотность вероятностив самой точке_. Значит во всякой точке, гденепрерывна, числосовпадает с естественно понимаемой плотностью вероятности в точке. Отсюда и название для функции- «плотность вероятности».

Непрерывные функции распределения, не имеющие плотностей, называются сингулярными.

Примеры непрерывных случайных величин:

1. Равномерное распределение на отрезке.

Случайная величина ξ имеет равномерное распределение на отрезке, если её плотность вероятности имеет вид

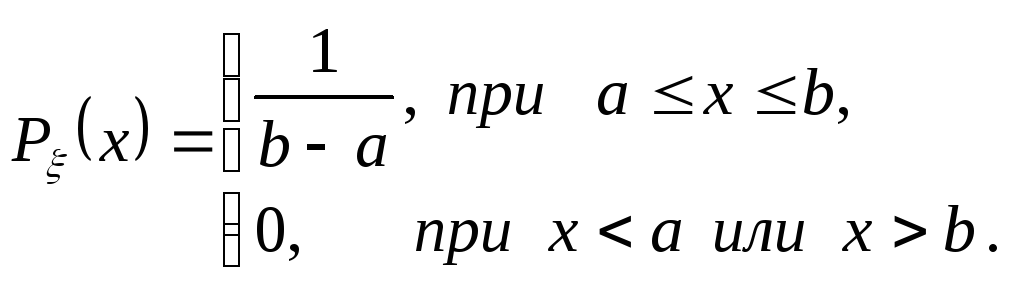(7)

Если какой-либо отрезок содержится в, то вероятность попадания в него случайной величины ξ равна:

. (8)

Таким образом, вероятность попадания в любую часть отрезкапропорциональна длине этой части.

Записав формулу (8) в виде

,

мы получим формулу геометрических вероятностей.

Следовательно, можно сказать, что геометрические вероятности порождаются равномерным распределением.

С равномерным распределением мы сталкивается всякий раз, когда по условиям опыта величина ξпринимает значение в конечном промежутке, причём все значения извозможны водинаковой степени (ни одно из них не имеет преимуществ перед другими). Например:

а) ξ– время ожидания на стоянке автобуса (величинаξраспределена равномерно на отрезке, гдеТ – интервал движения между автобусами.

б) ξ– ошибка при взвешивании случайно выбранного предмета, получающаяся от округления результата взвешивания до ближайшего целого числа (величинаξимеет равномерное распределение на отрезке, где за единицу принята цена деления шкалы).

Найдём функцию распределения равномерно распределенной случайной величины.

Связь между функцией распределения и плотностью вероятности даётся формулой (3)

.

Подставляя сюда функцию из (7) получим:

для ,,

для ,,

для .

Графики ипоказаны на рисунке 1.

Рис. 1

2. Нормальное (или гауссовское) распределение на прямой.

Случайная величина ξ имеет нормальное распределение с параметрами , если она имеет плотность:

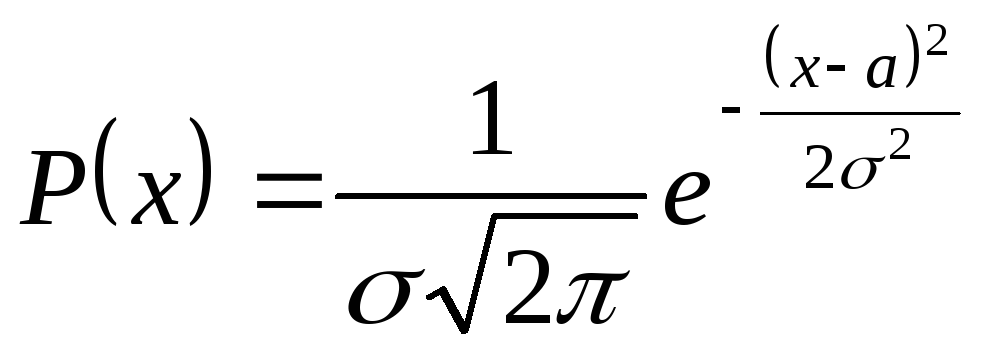. (9)

Нормальное распределение с параметрами (0,1) называется стандартным.

На рисунке 2 показаны графики функции P(x) для различных значений параметра σ.

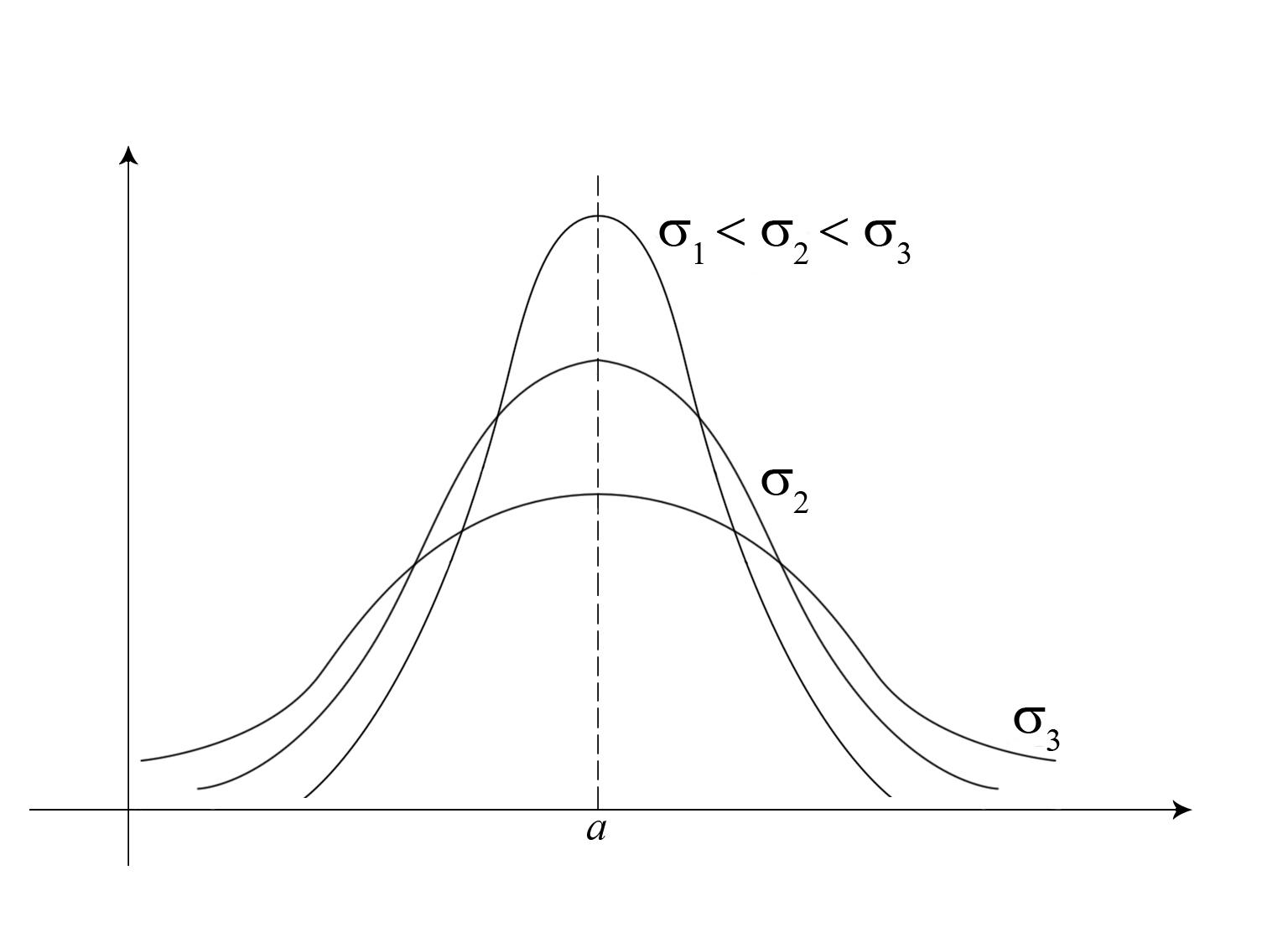Рис. 2.

Нетрудно проверить, что график P(x) имеет две точки перегиба: и .

В теории вероятностей и её приложениях нормальное распределение играет особо важную роль.

Решим теперь важную задачу. Пусть случайная величина ξ распределена по нормальному закону с параметрами .

Найдём вероятность попадания величины ξ в произвольный отрезок .

Имеем:

.

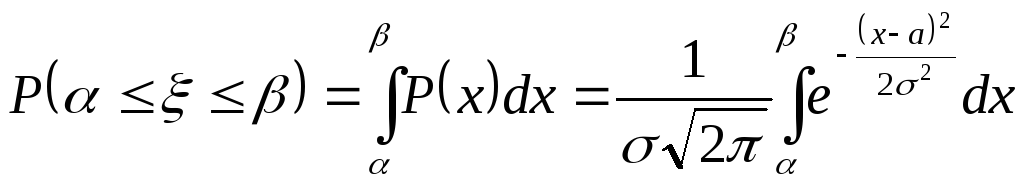Если в последнем интеграле произвести замену, то получим:

,

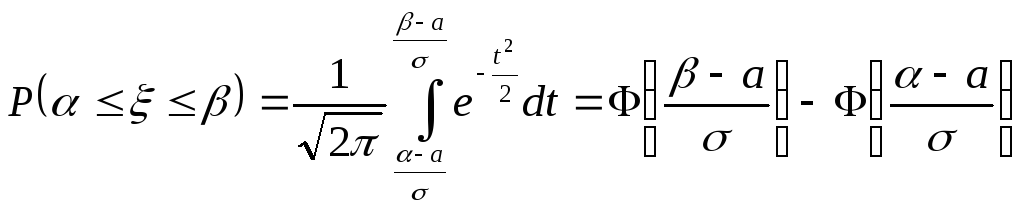где Ф(х) есть функция Лапласа, введенная в §12 гл.1

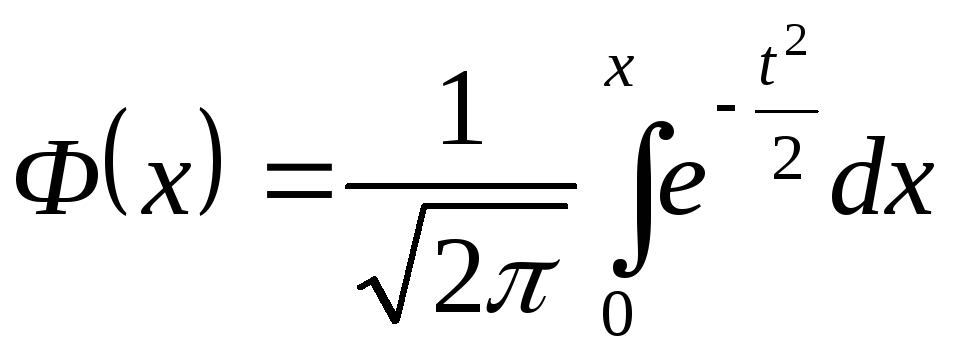. (10)

Таким образом, имеет место формула:

, (11),

которая и решает поставленную задачу.

В частности, вероятность попадания в отрезок будет равна:.

Эта вероятность отличается от 1 на весьма малую величину. Отсюда следует, что событие является практически достоверным, т.е., что практически возможные значения величины ξ расположены на отрезке .

Этот факт носит название: правило трёх сигм.

Из формулы (11) нетрудно видеть, что справедлива формула:

. (12)

С помощью этой формулы можно находить вероятность попадания величины ξ на участок, симметричный относительно точки а.

3. Показательное распределение.

Распределение с плотностью 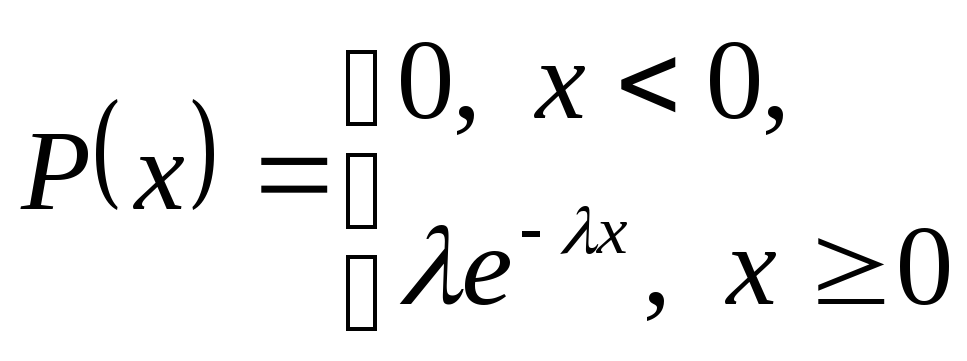называется показательным распределением.

Пользуясь формулой (3) получим, что функция распределения показательного закона имеет вид:

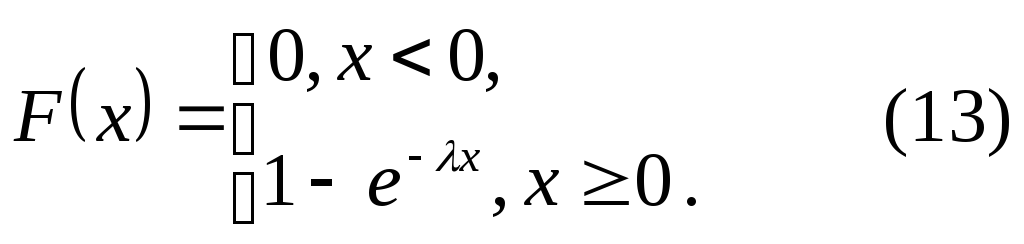
Вероятность попадания в интервал случайной величины , распределённой по показательному закону, будет равна:

. (14)

Пример. Пусть устройство начинает работать в момент времени , а в момент t происходит отказ.

Часто случайная величина Т-длительность безотказной работы устройства имеет показательное распределение, функция распределения которого:

(15)

определяет вероятность отказа устройства за время длительности t.

Функцией надёжности называют функцию, определяющую вероятность безотказной работы устройства за время длительности t:

. (16)

Параметр λ в формулах (15) и (16) равен интенсивности отказов (среднее число отказов в единицу времени).