2. Математическое ожидание случайной величины, имеющей плотность вероятности.

Пусть плотность распределения случайной величины есть. Разобьем числовую ось на малые отрезки точкамих_к , где, и положим

(рис. 2).

Определим новую дискретную случайную величину принимающую значениях_кпо одному в каждом отрезкепричем вероятность значениях_кравна вероятности попадания величины ξ в отрезок [х_к,х_к+1]

=.

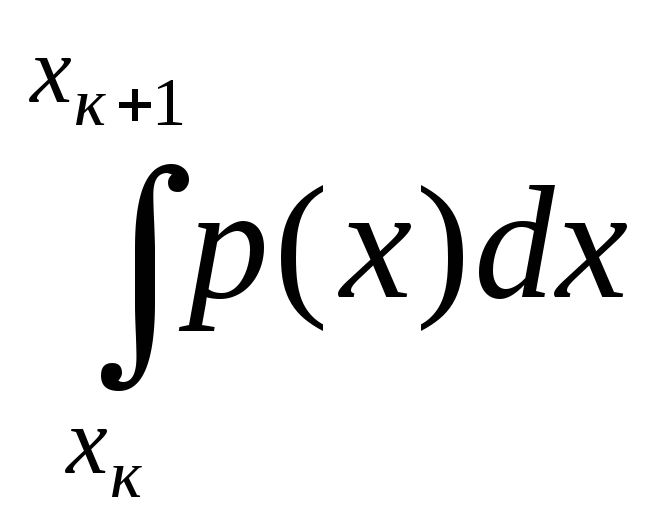Условие , обязательное для дискретного распределения, выполняется, поскольку

.

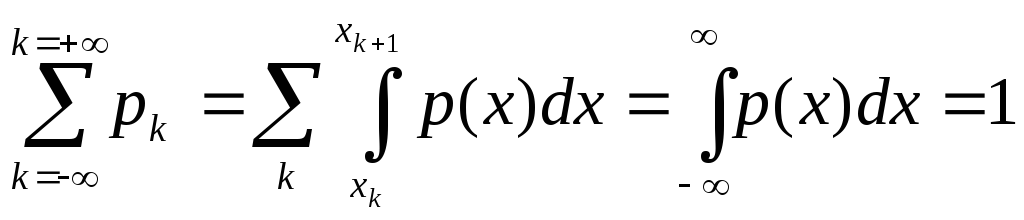Случайную величину будем называть-приближением к случайной величинеξ .

Замечание.Если величинаξсвязана с некоторым опытом, то взаимоотношения междуξиможно истолковать следующим образом. Пусть произведен опыт, и в результате его величинаξприняла значение, принадлежащее некоторому промежутку [х_к,х_к+1] (x[х_к,х_к+1]). Тогда величинапо определению принимает в том же опыте значения. При таком определении события (=x_к) и (ξ[х_к,х_к+1]) будут равны, и следовательно будут совпадать и вероятности этих событий. Это как раз и соответствует данному выше определению величины. Итак величинаполучается путем округления значений, принимаемых величинойξ, до ближайшей слева точких_котрезка [х_к,х_к+1], куда попадает это значение.

Отсюда, между прочим, видно, что переход от случайной величины ξк дискретной случайной величинеимеет вполне реальный смысл. Например, такой переход совершается всякий раз, когда значения величиныξ считываются с измерительного прибора, причём показания прибора округляются до ближайшего слева деления шкалы.

Наши рассуждения показывают, что по мере приближения к нулю различие междуиξ становятся все менее существенными. Поэтому естественно принять такое определение.

Определение.Математическим ожиданием случайной величины ξназывается число

.

Если указанный предел не существует, то математическое ожидание величины ξтакже считается несуществующим.

Итак мы получаем.

Mξ=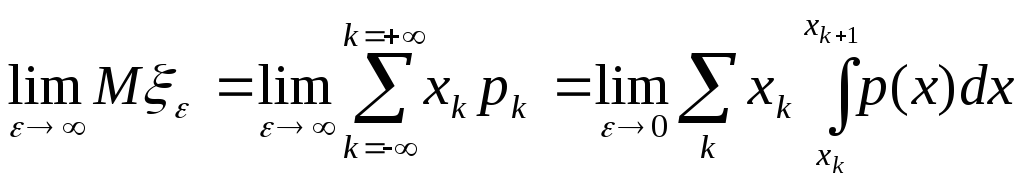. (1*)

Покажем, что предел в (1*) равен

. (2*)

Сравним по модулю к-ые члены рядов (1*) и (2*)

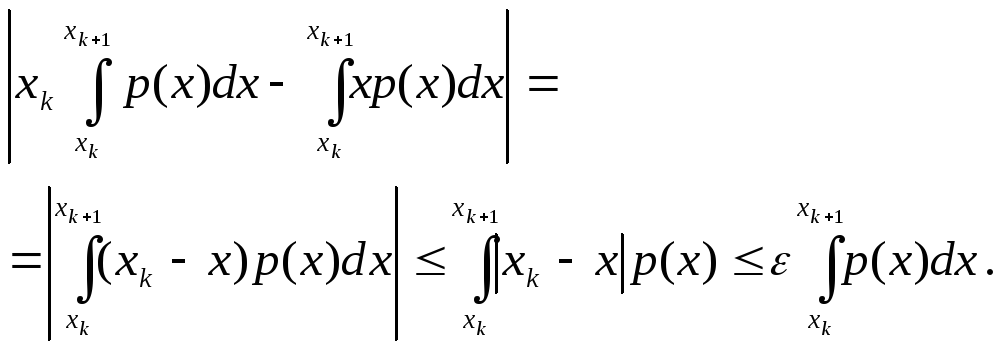
Следовательно

Итак, мы получили следующую формулу для математического ожидания величины

Мξ =(7)

Заметим, что мы использовали формулу математического ожидания для ДСВ

, (2*)

а она будет верна (см. определение 1) если ряд (2*) будет абсолютно сходится. Далее, для сходимости ряда достаточно требовать сходимости интеграла

.

Таким образом мы получили.

Теорема 1.Пустьξ– непрерывная случайная величина распределённая с плотностьюp(x). Если сходится интеграл, то существуетMξи справедлива формула

Mξ=. (8)

Аналогично теореме 1, доказывается теорема 2.

Теорема 2. Пустьξ- непрерывная случайная величина, распределённая с плотностьюp(x).Если сходится интеграл, то существует математическое ожиданиеMφ(ξ)случайной величиныφ(ξ)и имеет место формула.

M=. (9)

Пример 1.Найти математическое ожидание случайной величиныξ, равномерно распределённой на отрезке [a, b] .

Решение.Имеем.

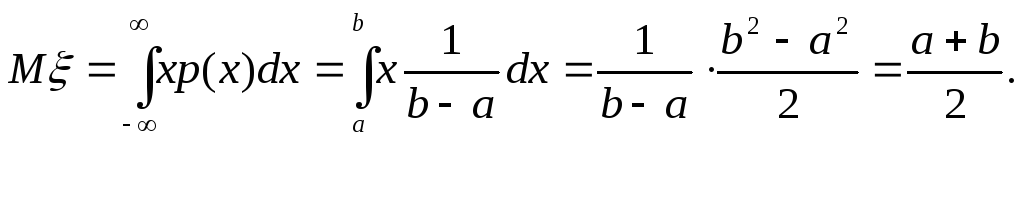
Мы получили, таким образом, что числу Mξсоответствует середина отрезка [a,b]. Ввиду равномерности распределенияξна отрезке [a, b] такой ответ ожидаем.

Можно показать, что математическое ожидание случайной величины , распределенной по нормальному закону с плотностью

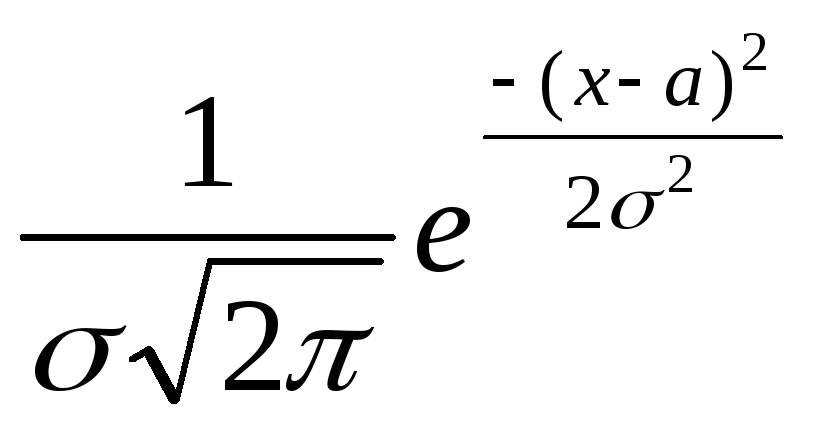=, (10)

равно параметру а, входящего в выражение (10) для нормального закона.

Пример 2.Распределение Коши. Плотность распределения Коши имеет вид

=.

Значит

M

Этот интеграл не является абсолютно сходящимся, и, значит, среднее значение для распределения Коши не существует.

Чтобы сделать аппарат числовых характеристик более эффективным, необходимо изучить их свойства. Приведём свойства математического ожидания.

Основные свойства математического ожидания.

1. Если случайная величина может принимать только одно значение С, то

M ξ =МС=С .(11)

Действительно, постоянную величину ξ=Сможно рассматривать, как дискретную величину, принимающую только одно постоянное значение х₁=Сс вероятностью 1. Но тогдаM ξ =С·1=С.

2. Постоянный множитель C можно выносить за знак математического ожидания:

M(C)=СM

Для ДСВ равенство (12) очевидно. Справедливость формулы для произвольной случайной величины (имеющей математическое ожидание) теперь легко вытекает из общего определения математического ожидания.

3. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий.

M(ξ₁+ξ₂)=. (13)

Докажем свойство (13) для ДСВ . Пусть- возможные значения величиныξ₁и…- возможные значенияξ₂. Возможные значения величиныξ=ξ₁+ξ₂будут содержаться среди чиселzвидаx_i+y_jпричем

,

где есть вероятность события (ξ₁=x_i, ξ₂=y_j) (см. §5). Значит

M.

Здесь суммирование сначала производится по тем парам (i,j), для которыхx_i+y_j=z_k; поэтому можно заменить во внутренней суммеz_kнаx_i+y_j, т.е.

M.

Затем суммирование производится по всем k, так что в итоге суммирование распределяется уже на все пары индексов (i,j), какова бы ни была суммаx_i+y_j, т.е.

В правой части (15) две суммы: в первой из них будем суммировать сначала по j, а затем поi, во второй – наоборот:

В силу формул (5) §5 гл.II

и значит

M.

Если ξ₁ иξ₂ непрерывные случайные величины, имеющие плотности, то это свойство также доказывается, если использовать формулы композиции (5) из §6 гл.II.

Формула (13) переносится на любое конечное число слагаемых

M(ξ₁+…+ξ_n) =Mξ₁+…+M ξ_n .

4. Если случайные величины ξ₁ иξ₂ независимы. То математическое ожидание их произведения равно произведению их математических ожиданий, т.е.

M(ξ₁ξ₂)=(Mξ₁)(Mξ₂). (16)

При доказательстве ограничимся случаем, когда система (ξ_1,ξ₂ ) дискретного типа.

Если ξ₁ иξ₂ – дискретны, то тогда дляξ=ξ₁·ξ₂применив такие же рассуждения, как и при выводе формулы (15), получим равенство

M(ξ₁·ξ₂)=.

Ввиду независимости величин ξ₁ иξ₂ имеем:

Обозначив,

,

получим

В правой части полученного равенства члены суммируются, в конечном счете, по всем возможным парам (i,j), суммируя сначала поj, а затем поiимеем:

что и требовалось доказать.

Найдем математическое ожидание биномиального распределения (см. пример 1.), используя свойство 3.

Рассмотрим схему Бернулли: Производится nнезависимых опытов. В каждом из них с одной и той же вероятностьюpможет появиться некоторое событиеА. Требуется найти математическое ожидание случайной величиныξ- числа наступлений событияАвnопытах .

Решение. Обозначим через ξ_iчисло наступлений событияАвi- м опыте (i=1,2,...,n). Очевидно,

ξ=ξ₁+ξ₂+…+ ξ_n.

Закон распределения каждой из величин ξ₁,ξ_2,…,ξ_nодин и тот же.

Значение ξi	0	1
Вероятности	q	p

где q=. СледовательноMξ_i=0q+1·p=p.По формуле сложения математических ожиданий имеем:

Mξ=Mξ₁+ Mξ₂+…+ Mξ_n=np. (17)

Пример 3.Случайное отклонение размера детали от стандарта подчиняется нормальному закону с параметрамиa=0, σ=5мк. Годными считаются детали, для которых отклонение не превышает 10мк. Определить среднее число годных деталей из ста выбираемых наудачу.

Решение.Обозначим черезАсобытие, состоящее в том, что деталь оказалась годной. Тогда (см. (12) §3 гл.II)

,

где ξобозначает отклонение размера детали от стандарта. По условию выбирается 100 деталей. Если рассматривать выбор каждой детали как отдельный опыт, то можно сказать, что производится 100 опытов. Нас интересует среднее число (математическое ожидание) наступлений событияАв этих опытах. Применив формулу (17), найдём, что это число равно