Глава II. Случайные величины и их

Характеристики

§1. Случайная величина и её функция

Распределения

В главе I мы встречались со случайными событиями, состоящими в появлении в результате опыта некоторого числа. Так в серии из nвыстрелов событие состоит вкпопаданиях в мишень, при бросании игральной кости выпадало то или иное число очков и т.д.В подавляющем большинстве случаев важные для приложений случайные события могут быть описаны числом ξ. При этом случайный характер исхода опыта влечет за собой случайность числаξ; это означает, что при повторении опыта оно меняется непредвиденным образом. Например:

1. Бросается игральная кость; ξ– выпавшее число очков.

2. Пусть в урне имеется Nшаров, из нихmбелых, остальные чёрные. По схеме выборки без возвращения из урны извлекаетсяnшаров. Тогдаξ– число белых шаров в выборке.

3. Электрическая лампочка испытывается на длительность горения; ξ- время горения лампочки.

4. Некто приходит на платформу станции метро, чтобы сесть в поезд; ξ– время ожидания ближайшего поезда.

5. Результат любого измерения выражается случайным числом ξ(ввиду невозможности исключить различные случайные воздействия).

Введём понятие случайной величины.

Определение 1. Случайной величиной, связанной с данным опытом, называемая величина, которая принимает то или иное числовое значение в зависимости от исхода опыта, заранее неизвестно, какое именно (это зависит от случая).

Замечание. Поскольку результатом опыта является одно и только одно элементарное событиеωиз пространства элементарных событий Ω ( см.§5), то случайная величина ξ представляет собой функцию от элементарного события. Поэтому мы можем дать следующее определение случайной величины.

Определение 2.Числовая функция от элементарного события называетсяслучайной величиной.

Различные случайные величины могут иметь одно и тоже множество возможных значений, но этого недостаточно для полного описания случайной величины. Необходимо знать, как часто случайная величина принимает то или другое из своих значений. Любое правило, устанавливающее связь между возможными значениями случайной величины и их вероятностями, называетсязаконом распределения случайной величины.

Пусть дана случайная величина ,. Зададим действительное числои рассмотрим событие -).

Замечание. В случае задания вероятностной схемы(см.§5), в определении случайной величинымы требуем чтобыбыло событиемдля любого.

Наиважнейшей (определяющей) характеристикой случайной величины является её функция распределения.

Определение 3.Функция

(1)

определенная при всех , называетсяфункцией распределения случайной величины.

С помощью функции распределения F(x)можно выразить вероятности попадания величины ξ в различные промежутки вида:

. (2)

Пусть . Тогда из разложения событияна сумму несовместных событийследуети значит

. (3)

Формула (3) в дальнейших рассуждения играет важную роль.

Теорема 1. Функция распределенияF(x)обладает следующими свойствами:

1. F(x) не убывает,

2. F(x)непрерывна слева, т.е.,

3. .

Доказательство.

Свойство 1 следует из формулы (3) (если учесть, что ).

Событие можно представить как счётную сумму несовместных событий

и т.д., где возрастающая последовательность, сходящаяся кх₀(например). Тогда получаем

Данный ряд сходиться (см.§5) и значит его сумма есть предел последовательности частичных сумм

.

Таким образом получаем, что

Это доказывает свойство 2.

Свойство3. Доказывается аналогично свойству 2.

Теорема доказана.

Представляет интерес вопрос о разрывах функции F(x). Точки разрыва соответствуют таким значениемх, для которых разностьотлична от нуля. Имеет место

Теорема 2. При любом значениихимеет место формула

. (4)

Доказательство. Рассмотрим убывающую последовательность, сходящуюся к точкех₀. Тогда событиеможно представить в виде счётной суммы несовместных событийт.е.

и значит (в виду счётной аддитивности вероятности см.§2)

.

Поскольку ряд сходится, то значит его сумма есть предел частичных сумм, т.е.

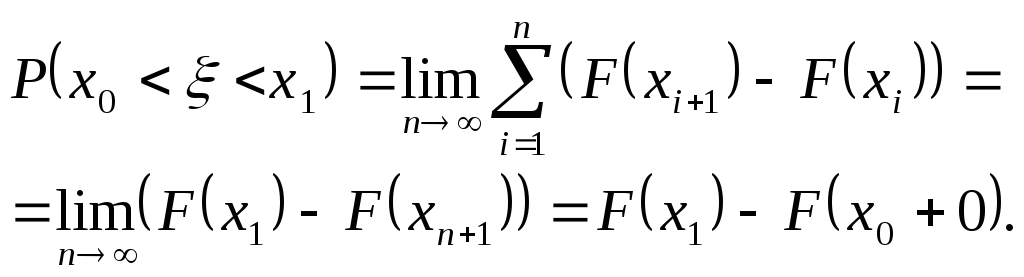
Отсюда получаем

и значит (в виду теоремы 1) получаем

.

Теорема доказана.

Итак скачок функции распределения в точке хсовпадает с вероятностью события(Рис.1)

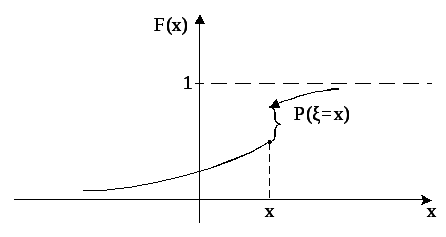
Рис. 1

Следствие.Еслих₀, точка непрерывности функцииF(x), то вероятность событияравна нулю (поскольку в этой точке).

Оказывается свойства 1-3 из теоремы 1 функции распределения F(x)являютсяхарактеристическими.

А именно, справедлива следующая важная теорема.

Теорема 3.Пусть дана функцияF(x),определённая для всех значенийхи обладающая свойствами:

1. F(x)не убывает,

2. F(x)непрерывна слева при любомх,

3. .

Тогда существует, и притом лишь одна, случайная величина , функция распределения которойсовпадает сF(x).