Глава I. Основные понятия и формулы теории вероятностей.

§1. Предмет теории вероятностей. Случайные события.

Предметом теории вероятностей являются модели опытов (экспериментов, наблюдений, испытаний), которые осуществляются, как только создаются определённые совокупности условий.

Примеры опытов:

1. бросание монеты 20 раз,

2. покупка лотерейного билета,

3. приход утром (между 8 и 9 часами) на станцию метро «Новогиреево»,

4. день 1 января,

5. день 1 января 2010 года.

На практике часто встречаются такие ситуации, когда исход проводимого нами опыта нельзя предсказать заранее с полной уверенностью. Например (смотри примеры опытов выше)

1. невозможно предсказать, что герб выпадет ровно 9 раз, или герб выпадет от 7 до 15 раз

2. выпадет ли выигрыш на лотерейный билет с таким-то номером

3. мы будем ждать электропоезд от 20 до 80 секунд

4. невозможно предсказать, что 1 января в Москве пойдёт снег.

Во всех подобных ситуациях мы вынуждены считать результат опыта зависящего от случая, рассматривать его как случайное событие.

Определение.Некоторое событие называется случайным по отношению к данному опыту, если при осуществлении этого опыта оно может наступить, а может и не наступить.

Примером случайного события может служить выпадение герба ровно 9 раз в опыте с бросанием монеты 20 раз, выигрыш проданному лотерейному билету, будем ждать поезд от 20 до 80 секунд, совпадение даты рождения (в опыте) у двух наугад выбранных студентов на лекции по теории вероятностей и в данной аудитории.

Случайные события обозначаются в дальнейшем А,В,Си т.д.

Замечание.Согласно данному выше определению, событие считают случайным, если его наступление в результате опыта представляет собой лишь одну из двух возможностей – оно либо наступит, либо не наступит.

События, которые в результате данного опыта всегда наступают, называется достоверными(обозначениеI), которые никогда не наступают –невозможнымисобытиями (обозначение Ø).

Теория вероятностей рассматривает модели таких опытов, которые могут быть повторены в одних и тех же условиях (достаточно) неограниченное число раз, т.е. мы будем предполагать, что в принципе возможно создать много раз одни и те же условия, осуществляющие данный опыт.

Случайные события, наступление которых возможно в такого рода опытах, называются массовыми случайными событиями.

Массовые случайные события следует отличать от единичных, обладающих той особенностью, что опыт, с которым связаны эти события, принципиально невоспроизводим. Например, событие «1 января 2010 г. в Москве шел снег» является в этом смысле единичным (исключительным), так как воспроизвести наступление указанного дня много раз невозможно. В то же время событие « 1 января в Москве шёл снег» (без упоминания о годе) является несомненно, массовым: ведь наблюдать погоду в Москве 1 января можно много раз (в течение многих лет).

В самых общих словах предмет теории вероятностей может быть определён следующим образом:

Теория вероятностей занимается изучением закономерностей, присущих массовым случайным событиям.

Оказывается, и случайные события подчиняются некоторым (вероятностным) закономерностям. Исход каждого опыта по отношению к данному событию является случайным, неопределённым. Однако средний результатбольшого числа опытов утрачивает случайный характер, становится закономерным.

Например, рассмотрим опыт с бросанием данной монеты. Предположим, что бросание производится много раз подряд. Оказывается «доля» (средний результат) тех бросаний, при которых выпадает герб (т.е. отношение числа таких бросаний к числу всех бросаний) с увеличением числа бросаний приближается к (или другому числу – это зависит от состояния монеты).

Приведём другой пример. В сосуде заключён газ. Находясь в беспрерывном движении, молекулы газа ударяются друг о друга и вследствие этого постоянно меняют величину и направление своей скорости. Казалось бы, отсюда следует, что давление газа на стенки сосуда, обусловленное ударами отдельных молекул о стенки, должно меняться случайным, неконтролируемым образом. Однако это не так: давление газа подчиняется строгой закономерности (закону Бойля-Мариотта). Причина этой закономерности кроется в том, что давление газа на стенки сосуда есть средний результат воздействия большого числа молекул. Случайные особенности, свойственные движению отдельных молекул, в массе (поскольку молекул много) взаимно погашаются, нивелируются и возникает некоторая средняя закономерность.

Именно эта устойчивость среднего результата, его независимость от колебаний отдельных слагаемых (отдельных исходов опыта) и обуславливает широту применения теории вероятностей. Физика, биология, медицина, лингвистика и т.д.- все эти области науки используют (одни в большей степени, другие в меньшей) понятия и выводы теории вероятностей и родственных ей дисциплин - математической статистики, теории информации и т.д.

Перейдём теперь к простейшей, самой главной закономерности в случайных событиях, в конечном счёте, составляющей основу всех приложений теории вероятностей к практике.

§ 2. Вероятность случайного события.

Сравнивая между собой случайные события, мы часто говорим, что одно из них более вероятно (имеет больше шансов наступить, в большей степени возможно), чем другое. Например: при игре в карты при сдаче каждому игроку 6 карт событие получить 2 туза более вероятно, чем получить 4 туза.

Чтобы придать подобным сравнениям количественный смысл, необходимо с каждым событием связать число, выражающую степень возможности данного события.

Пусть А есть случайное событие по отношению к данному опыту. Пусть данный опыт произведен N раз и при этом случайное событие А наступило N(А) раз.

Число N(А) называется частотой события А в рассматриваемой серии опытов.

Составим отношение:

. (1)

Оно называется относительной частотой наступления события А в N опытах.

Оказывается, для весьма многих (практически для всех) случайных массовых событий А относительная частота обладает свойством устойчивости, которое состоит в том, что в нескольких сериях из достаточно больших наблюдений событияА (в одних и тех же условиях) мы обычно имеем приближённые равенства

.

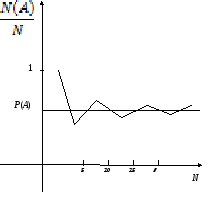
Это означает, что с увеличением числа опытов N, относительная частота стабилизируется (колеблется около одного и того же числа), приближаясь к некоторой постоянной P(A), которая характеризует данное случайное событие А. Естественно считать, что эта постоянная и измеряет степень возможности наступления события А. Она называется вероятностью события А. Итак мы получили следующее:

Определение. Вероятность случайного события А - это связанное с данным событием постоянное число, обозначаемое через P(А), около которого колеблется относительная частота наступления этого события в длинных сериях опытов.

Это определение можно выразить в виде формулы:

. (2)

Замечание. Необходимо предостеречь от неправильного понимания формулы (2). В этой формуле отнюдь не утверждается , что предел равенP(A). Что для сколь угодно малого , начиная с некоторого номера N₀, будет выполнятся неравенство . Эту формулу мы должны понимать следующим образом: если выполнить большое число серий опытов, состоящих из достаточно большого количества опытов, то для подавляющего большинства серий относительная частота будет отличатся отP(A) меньше чем на . Однако могут существовать и такие «исключительные» серии для которых сильно отличается отP(A). «Исключительные» серии составляют незначительную часть от общего числа серий. Поэтому можно считать практически достоверным, что наша серия (при большом N) не окажется «исключительной» и что в ней будет близко кP(A).

Здесь мы использовали важное в приложениях теории вероятностей правило, по которому события с очень малой вероятностью считаются практически невозможными.

Замечание. Устойчивость относительной частоты представляет собой одну из простейших и в то же время основных закономерностей, проявляющихся в сфере «случайного». В дальнейшем все основные (их всего 3) формулы теории вероятностей (из которых следует все формулы этой теории, включая самые сложные) мы получим исходя из этой закономерности.

Устойчивость частот – это объективное свойство массовых случайных явлений окружающего нас реального мира. Отсутствие устойчивости частот в сериях испытаний свидетельствует о том, что условия, при которых производятся испытания, претерпевают значительные изменения (другими словами мы проводим разные опыты).

Таким образом, теория вероятностей является математической моделью окружающего нас (реального) мира в сфере «случайного».

Замечание. Приведённое выше определение вероятности наилучшим образом соответствует потребностям приложений и отражает объективный характер вероятности. Другими словами, если найденная путем некоторого расчёта (по формулам теории вероятностей) вероятность события А равна числу p, то реальная ценность этого результата состоит прежде всего в возможности такого предсказания: при большом числе опытов относительная частота наступления события А будет близка к p.

§ 3. Алгебра событий

При нахождении вероятностей приходится учитывать связи между событиями. Наиболее простые из них заключаются в том, что одни события являются комбинациями других. Рассмотрим три вида основных комбинаций: сумма событий, произведение событий, переход к противоположному событию.

Пусть с некоторым опытом связаны события А и В.

1. Сумма событий. Суммой (или объединение) событийА иВназовём событие, обозначаемоеА+В(илиА В), которое наступает тогда и только тогда, когда наступает или событиеАили событиеВ(или оба вместе).

2. Произведение событий. Произведением (или пересечением) событийАиВназовём событие, обозначаемоеAB(или), которое считается наступившим тогда и только тогда, когда наступают оба событияАиВ. Другими словами,АВесть совместное наступление событийАиВ.

3. Противоположное событие. Событие назовём событием, противоположным к событиюА, если оно наступает тогда и только тогда, когда событие А не наступает.

4. Равенство событий. События А и В считаются равными, если всякий раз, когда наступает одно из них наступает и другое.

Замечание. Чаще всего равные события имеют отличающиеся по форме словесные описания. Например, событие «не все студенты данного курса успешно сдали экзамен по теории вероятностей» и событие «по крайней мере один из студентов данного курса не сдал теорию вероятностей» равны, хотя и выражены различными оборотами речи.

Пример 1. Опыт заключается в бросании игральной кости. При бросании может выпасть число очков, равное какому либо числу из множества чисел {1,2,3,4,5,6}. Рассмотрим в этом случае следующие события:

А = {выпадение чётного числа очков}

В = {выпадение нечётного числа очков}

С = {выпадение числа очков больше трех}

Тогда.

А+В ={выпадение числа очков равное или 1, или 2, ..., или 6}= - достоверное событие

А+С = {выпадение числа очков, равное или 2 или 4 или 5 или 6}

АВ = Ø - невозможное событие

АС = {выпадение числа очков равное или 4 или 6}

= {выпадение нечётного числа очков}= В.

Пример 2. Этот пример важен для наглядного истолкования соотношений между событиями. В некоторую область D на плоскости (например квадрат) случайно бросается точка. В этом случае каждое событие рассматривается как попадание случайно брошенной точки в некоторую область D ₁ области D. Иначе говоря, каждое событие задаётся некоторой фигурой в области D. При таком истолковании событие А+В будет, не что иное, как попадание точки в область, являющуюся объединением фигур А и В (рис.1), событие АВ - попадание в область, являющуюся пересечением фигур А и В, а событие – попадание в областьдополнительную к фигуре А (на рис. 1, соответствующие области заштрихованы)

Событие А = {попадание точки в круг А}

СобытиеВ = {точка попадает в треугольник В}

Беря несколько событий А,В,С,D, … и применяя к ним в любом порядке операции сложения, умножения, переход к противоположным событиям, можно строить различные комбинации, например: .

Укажем наиболее важные свойства операций над событиями.

Первые две формулы (формулы де Моргана) являются основными, они связывают сразу все три операции.

1. - дополнение до суммы есть произведение дополнений

2. - дополнение до произведения есть сумма дополнений

3.- коммутативность

4. - ассоциативность

5. - дистрибутивность

6.

7.