§ 4. Функции от случайной величины.

Определение.Множество точек на числовой прямойRназываетсяборелевскимесли оно может быть получено из множеств видаприменением конечного или счётного числа операций объединения, пересечения и дополнения.

Класс борелевских множеств достаточно широк. В нём содержатся множества вида:

Практически все встречающиеся в приложениях числовые множества являются борелевскими.

Пусть (Ω, S,P) произвольная вероятностная схема (связанная с некоторым опытом) и- случайная величина. Рассмотрим числовую функцию. Подставляя вместохслучайную величину ξ, мы получим новую случайную величину.

На функцию наложим ограничение: для любого борелевского множестваВмножествоявляется событием, т.е. принадлежитS.

К множеству таких функций принадлежат, в частности, непрерывные и кусочно непрерывные функции (непрерывные функции на числовой прямой за исключением конечного числа точек разрыва 1-го рода). В дальнейшем мы такие функции и будем рассматривать.

Рассмотрим пример, когда случайная величина есть ДСВ или НСВ.

Пример 1.Пустьξесть ДСВ и- возможные значенияξ, а- их вероятности. Тогда множество значений случайной величиныбудет состоять из множества чисел. Среди этих чисел могут быть совпадающие. Подсчитаем теперь вероятности различных значений величиныη.

Пусть, тогда событиеесть сумма несовместных событий видаи, значит:

(1)

Итак, чтобы найти вероятность события , нужно из всех возможных значенийвеличиныξвыбрать те, для которыхи просуммировать их вероятности.

Пример 1.Пусть закон распределения величиныξимеет вид:

Значение	-2	-1	0	1	2	3
Вероятности	0,1	0,2	0,3	0,05	0,15	0,2

Найдём закон распределения случайной величины .

Возможные значения η будут: т.е. 0,1,4,9. Их вероятности будут равны:

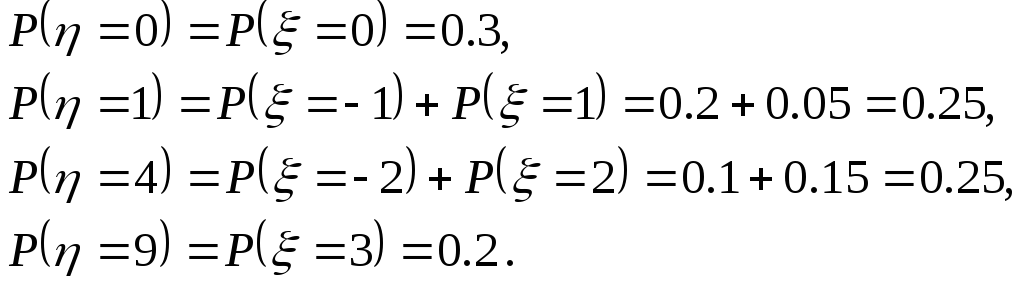
Следовательно, закон распределения для ηбудет:

Значение η	0	1	4	9
Вероятности	0,3	0,25	0,25	0,2

Рассмотрим ещё два примера вычисления функции распределения и плотностислучайной величиныпо функции распределенияи плотности.

Пример 2.Пусть функциямонотонно возрастает. Тогда у неё существует обратная функция, такая, что. Тогда, если, имеем:

(2)

Дифференцируя (2) по х, имеем (в предположении, чтодифференцируема и имеется плотность), используя производную для сложной функции:

=,

откуда получаем (используя производную для обратной функции) соотношение между плотностями

. (3)

В частности, при имееми значит плотность распределения случайной величиныимеет вид

.

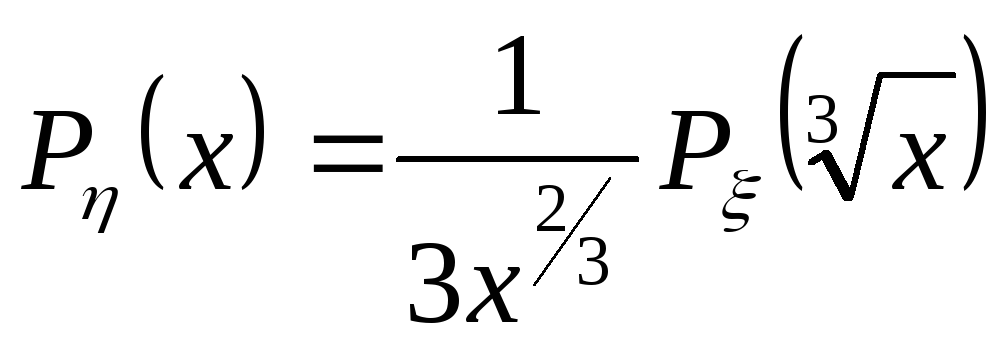Пример 3.Пусть–непрерывная функция распределения с плотностью.

В данном случае функция не является монотонной и, поэтому, нельзя применить формулу (3).

Вычислим непосредственно, исходя из её определения.

При имеем

При получаем

Беря производную от левой и правой частей, получаем, используя формулу для производной сложной функции:

при ,

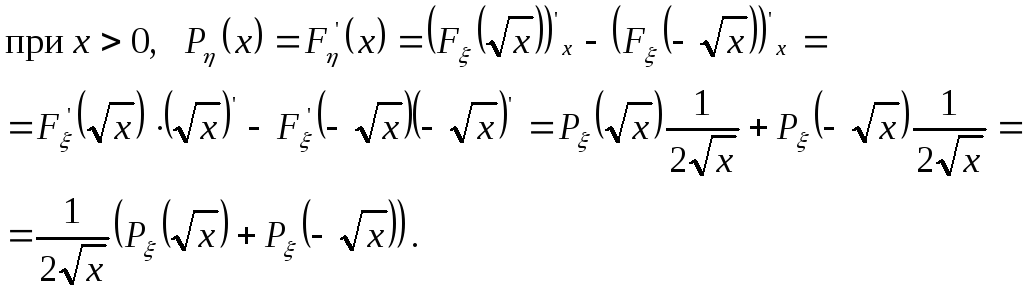
§ 5. Системы случайных величин.

В практических задачах часто встречается ситуации, при которых те или иные случайные величины приходится изучать совместно.

Систему из двух случайных величин можно истолковать как случайную точку на плоскости, систему трёх случайных величин– как случайную точку в трехмерном пространстве и т.д.

Ограничимся двумерным случаем; обобщение на любое число случайных величин не представляет особых затруднений.

Понятие системы двух случайных величин связано с представлением об опыте, результатом которого является пара чисел . Поскольку исход опыта есть случайное событие, то предсказать значения чиселиневозможно (при повторении опыта они меняются непредвиденным образом). Приведём примеры.

Пример 1.Дважды бросается игральная кость. Обозначим через, число очков при первом бросании, через– число очков при втором. Парабудет системой двух случайных величин или двумерной случайной величиной.

Пример 2.Из некоторой аудитории наугад выбирается один человек;-его рост (пусть в сантиметрах),- вес (в килограммах).

Пример 3.Сравниваются письменные работы по математике и физике:- оценка за работу по математике,- оценка за работу по физике.

Пример 4.Рассмотрим квартиры в многоэтажном доме, в которых есть семья (муж и жена). Выберем наудачу некоторую семью и обозначим через- возраст мужа,

–возраст жены, выраженные в целых числах лет. Возможные значения ,здесь можно считать целыми числами от 16 до 100.

Поскольку с каждым опытом связано некоторое вероятностное пространство (вероятностная схема см. § 5. гл.1) (Ω, S,P) , то рассмотрим на нём две случайные величины, где(в общем случае рассматриваетсяnслучайных величин). Так как множестваипринадлежатS, т.е. являются событиями, то и их пересечение (или, что

то же самое, произведение) . Поэтому существует вероятность этого события, которая называетсядвумерной функцией распределения.

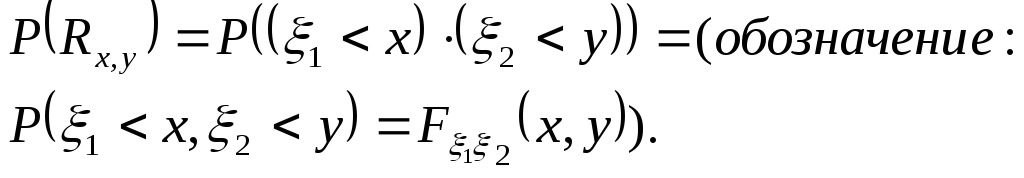(1)

В дальнейшем эту двумерную функцию распределения мы будем иногда записывать просто не указывая индексы,.

Системы случайных величин, чаще всего встречающиеся в приложениях, подразделяются на два типа: дискретные и непрерывные.