
Digital design with CPLD applications and VHDL (R. Dueck, 2000)
.pdf
80 C H A P T E R 3 • Boolean Algebra and Combinational Logic
DeMorgan’s Theorems
We have already seen DeMorgan’s theorems. We will list them again, but will not comment further on them at this time.
Theorem 20: xy x y
Theorem 21: x y x y
Other Multivariable Theorems
Theorem 22: x xy x
Proof:
x xy x (1 y) (Distributive property)
x 1 (1 y 1; Theorem)
x
FIGURE 3.29
Theorem 22
Figure 3.29 illustrates the circuit in this theorem. Note that the equivalent is not a circuit at all, but a single, unmodified variable. Thus, the circuit shown need never be built.
x |
x xy x |
|
|
y |
xy |
|
EXAMPLE 3.11 |
Simplify the following Boolean expressions, using Theorem 22 and other rules of Boolean |
|
|
algebra. Draw the logic circuits of the unsimplified and simplified expressions. |
|
|
a. |
H KL K |
|
b. Y (A B)CD (A B) |
|
|
c. |
W (PQR P Q)(S T) (P Q)(S T) (S T) |
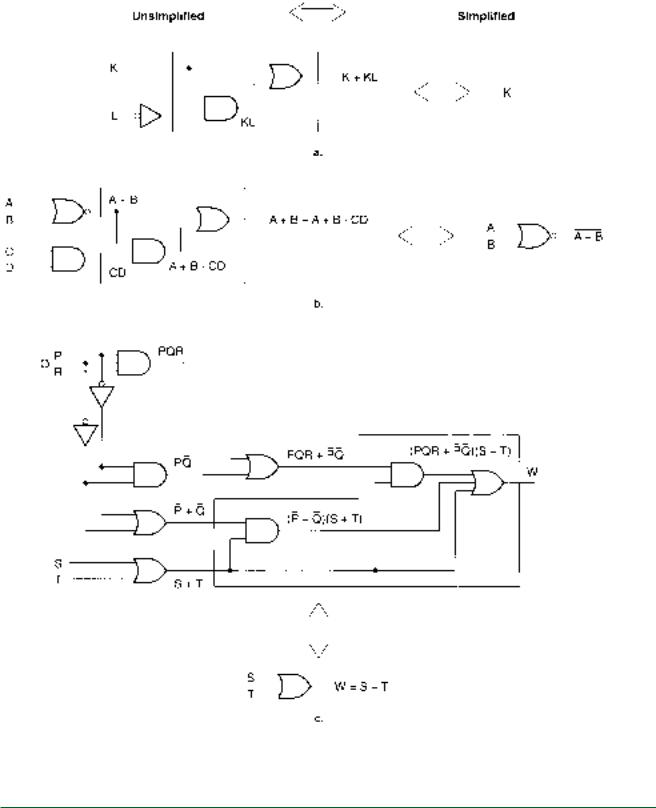
Solution Figure 3.30 shows the logic circuits for the unsimplified and simplified versions of the above expressions.
a. Let x K, let y L:
H x xy K KL
Theorem 22 states x xy x. Therefore K KL K. b. Let x (A B), let y CD:
Y x xy x A B
c.Let x S T, let y (P Q):
Since x xy x, (P Q)(S T) (S T) (S T).
W (PQR P Q)(S T) (S T)
Let x S T, let y (PQR P Q)
W x xy x S T
Alternate method:
W (PQR P Q)(S T) (P Q)(S T) (S T)
By the distributive property:
W ((PQR P Q) (P Q))(S T) (S T)
Let x S T, let y ((PQR P Q) (P Q)):
W x xy x S T
3.3 • Theorems of Boolean Algebra |
81 |
FIGURE 3.30
Example 3.11
Logic Circuits for Unsimplified and Simplified Expressions
82 C H A P T E R 3 • Boolean Algebra and Combinational Logic
Theorem 23: (x y)(x z) x yz
Proof: (x y)(x z) xx xz xy yz (Distributive property)
(x xy) xz yz (xx x; Associative property)
x xz yz (x xy x (Theorem 22))
(x xz) yz (Associative property)
x yz |
(Theorem 22) |
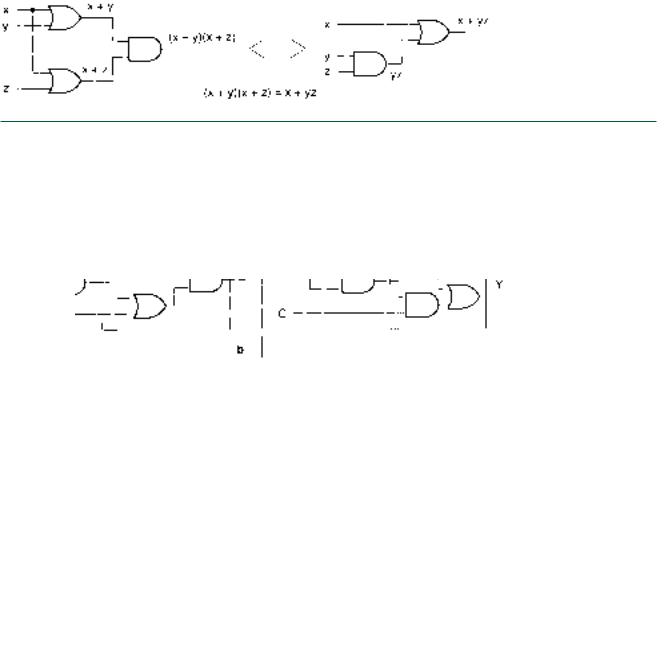
Figure 3.31 shows the logic circuits for the left and right sides of the equation for Theorem 23. This theorem is a special case of one of the distributive properties, Theorem 6, where w x.
FIGURE 3.31
Theorem 23
EXAMPLE 3.12 |
Simplify the following Boolean expressions, using Theorem 23 and other rules of Boolean |
|
algebra. Draw the logic circuits of the unsimplified and simplified expressions. |
|
a. L (M N)(M P) |
|
b. Y (A B AB)(A B C) |
|
Solution Figure 3.32 shows the logic circuits for the unsimplified and simplified ver- |
|
sions of the above expressions. |
FIGURE 3.32
Example 3.12
Logic Circuits for Unsimplified and Simplified Expressions
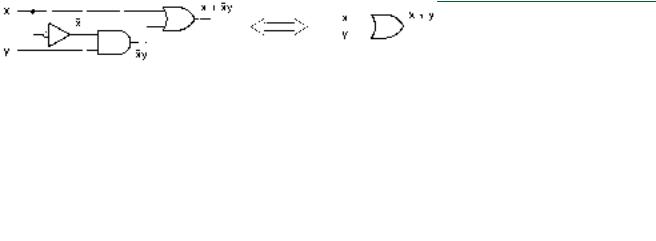
3.3 • Theorems of Boolean Algebra |
83 |
Theorem 23: (x y)(x z) x yz a. Let x M, let y N, let z P:
L (x y)(x z) x yz M N P
b. Let x A B, let y AB, let z C:
Y (x y)(x z) x yz A B ABC A B ABC
Theorem 24: x xy x y
Proof: Since (x y)(x z) x yz, then for y x:
|
|
|
x xy (x x)(x y) |
|
|
|
|
1) |
|
1 (x y) (x x |
|
x y
Figure 3.33 illustrates Theorem 24 with a logic circuit.
FIGURE 3.33
Theorem 24
|
|
|
N O T E |
|
|
|
|
|
|
|
Here is another way to remember Theorem 24: |
||||
|
|
|
If a variable (x) is ORed with a term consisting of a different variable (y) AND the |
||||
|
|
|
|
|
|
||
|
|
|
first variable’s complement (x), the complement disappears. |
||||
|
|
|
|
|
|||
|
|
|
|
|
x xy x y |
||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
EXAMPLE 3.13 |
Simplify the following Boolean expressions, using Theorem 24 and other rules of Boolean |
||||||
|
algebra. Draw the logic circuits of the unsimplified and simplified forms of the expres- |
||||||
|
sions. |
|
|||||
|
a. |
W U UV |
|
||||
|
b. P QRS (Q R S) T |
|
|||||
|
|
|
J KM (K L M) KM |
|
|||
|
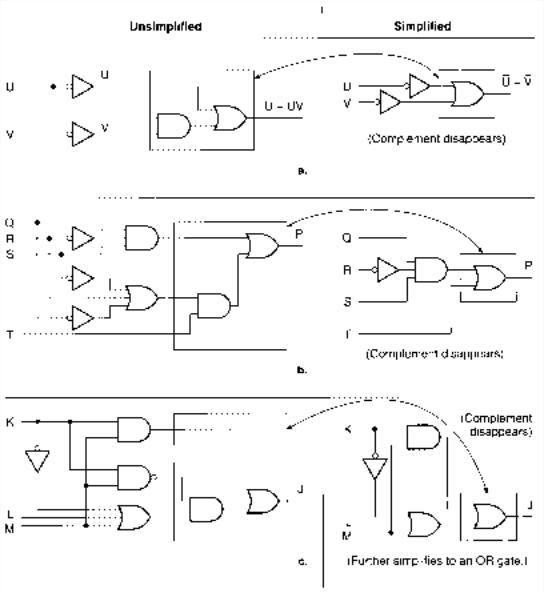
Solution Figure 3.34 shows the circuits for the unsimplified and simplified expressions. |
||||||
|
|
|
|
Theorem 24: x xy x y |
|||
|
|
|
|
|
|
|
|
|
a. Let x U, let y V: |
|
|||||
|
|
|
|
W x xy x y U V |
|||
|
|
|
|
|
|||
|
b. |
|
P QRS (Q R S) T |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
QRS Q RS T |
(DeMorgan’s theorem) |
||
|
|
|
Let x QRS, let y T: |
|
|||
P x xy x y QRS T
84 C H A P T E R 3 • Boolean Algebra and Combinational Logic
FIGURE 3.34
Example 3.13
Logic Circuits for Unsimplified and Simplified Expressions
c. Let x KM, let y (K L M): |
|
|
J x xy x y KM K L M |
|
|
|
|
|
K L (M KM) |
(Associative property) |
|
K L M |
(Theorem 22) |
|
|
|
The rules of Boolean algebra are summarized in Table 3.8. Don’t try to memorize all these rules. The commutative, associative, and distributive properties are the same

3.3 • Theorems of Boolean Algebra |
85 |
as their counterparts in ordinary algebra. The single-variable theorems can be reasoned out by your knowledge of logic gate operation. That leaves only five multivariable theorems.
Table 3.8 Theorems of Boolean Algebra
Commutative Properties
1.x y y x
2.x y y x
Associative Properties
3.x (y z) (x y) z
4.x(yz) (xy)z
Distributive Properties
5.x(y z) xy xz
6.(x y)(w z) xw xz yw yz
xAND/OR/XOR 0/1
7.x 0 0
8.x 0 x
9.x 0 x
10.x 1 x
11.x 1 1
12.x 1 x
xAND/OR/XOR x/ x
13.x x x
14.x x x
15.x x 0
16.x x 0
17.x x 1
18.x x 1
Double Inversion
19. x x
DeMorgan’s Theorems
20.xy x y
21.x y x y
Other Multivariable Theorems
22.x xy x
23.(x y)(x z) x yz
24.x xy x y
SECTION 3.3 REVIEW PROBLEMS
3.4Use theorems of Boolean algebra to simplify the following Boolean expressions.
a.Y AC (A C)D
b.Y A C ACD
c.Y (AB BC)(AB C)
86 C H A P T E R 3 • Boolean Algebra and Combinational Logic
Table 3.9 Truth Table for the SOP and POS Networks in Figure 3.35
A |
B |
C |
Y |
|
|
|
|
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
|
|
|
|
3.4 Simplifying SOP and POS Expressions
K E Y T E R M S
Maximum SOP simplification The form of an SOP Boolean expression that cannot be further simplified by canceling variables in the product terms. It may be possible to get a POS form of the expression with fewer terms or variables.
Maximum POS simplification The form of a POS Boolean expression that cannot be further simplified by canceling variables in the sum terms. It may be possible to get an SOP form of the expression with fewer terms or variables.
Earlier in this chapter, we discovered that we can generate a Boolean equation from a truth table and express it in sum-of-products (SOP) or product-of-sums (POS) form. From this equation, we can develop a logic circuit diagram. The next step in the design or analysis of a circuit is to simplify its Boolean expression as much as possible, with the ultimate aim of producing a circuit that has fewer physical components than the unsimplified circuit.
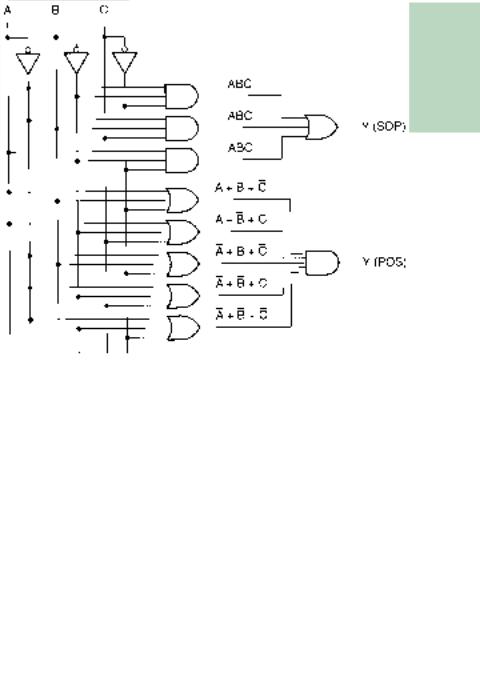
In Section 3.2, we found the SOP and POS forms of the Boolean expression represented by Table 3.9. These forms yield the logic diagrams shown in Figures 3.17 and 3.20. For convenience, the circuits are illustrated again in Figure 3.35. The corresponding algebraic expressions can be simplified by the rules of Boolean algebra to give us a simpler circuit in each case.
FIGURE 3.35
Unsimplified SOP and POS Networks
The sum-of-products and product-of-sums expressions represented by Table 3.9 are:
Y A B C A B C A B C (SOP)
and
Y (A B C)(A B C)(A B C)(A B C)(A B C) (POS)
3.4 • Simplifying SOP and POS Expressions 87 |
|
The SOP form is fairly easy to simplify: |
|
Y A B C A B C A B C |
|
(A A) B C A B C |
(Distributive property) |
1 B C A B C |
(x x 1) |
B C A B C |
|
(x 1 x) |
|
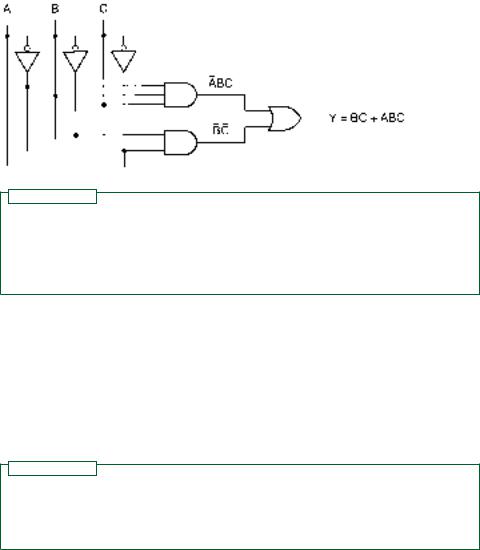
Since we cannot cancel any more SOP terms, we can call this final form the maximum SOP simplification. The logic diagram for the simplified expression is shown in Figure 3.36.
FIGURE 3.36
Simplified SOP Circuit
N O T E
Two terms in an SOP expression can be reduced to one if they are identical except for one variable that is in true form in one term and complement form in the other. Such a grouping of a variable and its complement always cancels.
xyz xyz xy(z z) xy
There is a similar procedure for the POS form. Examine the following expression:
Y (A B C)(A B C)
Recall Theorem 23: (x y)(x z) x yz.
Let x A B, let y C, let z C.
Y (A B) CC |
(Theorem 23) |
(A B) 0 |
|
(xx 0) |
|
(A B) |
(x 0 x) |
N O T E
A POS expression can be simplified by grouping two terms that are identical except for one variable that is in true form in one term and complement form in the other.
(x y z)(x y z) (x y) zz x y
Let us use this procedure to simplify the POS form of the previous Boolean expression, shown again below with the terms numbered for our reference. The numbered value of each term corresponds to the binary value of the line in the truth table from which it is derived.
(1) |
(2) |
(5) |
(6) |
(7) |
Y (A B C ) (A B C) (A B C ) (A B C) (A B C )
There can be more than one way to simplify an expression. The following grouping of the numbered POS terms is one possibility.

88 C H A P T E R 3 • Boolean Algebra and Combinational Logic
FIGURE 3.37
Simplified POS Circuit
(1)(5): (A B C) (A B C) B C
(2)(6): (A B C) (A B C) B C
(6)(7): (A B C) (A B C) A B
Combining the above terms, we get the expression:
Y (B C)(B C)(A B)
Figure 3.37 shows the logic diagram for this expression. Compare this logic diagram and that of Figure 3.36 with the unsimplified circuits of Figure 3.35. Since there are no more cancellations of POS terms possible, we can call this the maximum POS simplification. We can, however, apply other rules of Boolean algebra and simplify further.
Y (B C)(B C)(A B) |
|
(B AC)(B C) |
(Theorem 23) |
B B B C A B C A C C |
(Distributive property) |
B C A B C |
(x x 0) |
|
|
This is the same result we got when we simplified the SOP form of the expression. To be sure you are getting the maximum SOP or POS simplification, you should be
aware of the following guidelines:
1.Each term must be grouped with another, if possible.
2.When attempting to group all terms, it is permissible to group a term more than once, such as term (6) above. The theorems x x x (POS forms) and x x x (SOP forms) imply that using a term more than once does not change the Boolean expression.
3.Each pair of terms should have at least one term that appears only in that pair. Otherwise, you will have redundant terms that will need to be canceled later. For example, another possible group in the POS simplification above is terms (5) and (7). But since both these terms are in other groups, this pair is unnecessary and would yield a term you would have to cancel.
EXAMPLE 3.14 |
Find the maximum SOP simplification for the Boolean function represented by Table 3.10. |
|||||
|
Draw the logic diagram for the simplified expression. |
|
|
|||
|
Solution SOP form: |
|
|
|
|
|
|
(8) |
(9) |
(10) |
(11) |
(12) |
(14) |
Y A B C D A B C D A B C D A B C D A B C D A B C D
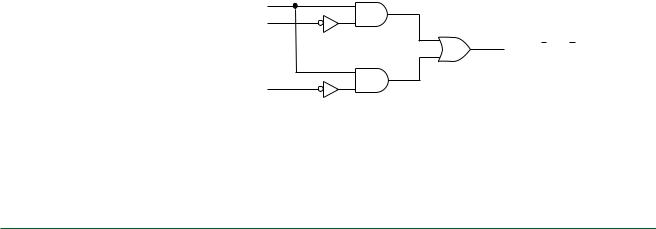
Table 3.11 Truth Table for Section Review Problem
A |
B |
C |
Y |
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
|
|
|
|
3.4 • Simplifying SOP and POS Expressions |
89 |
Table 3.10 Truth Table for
Example 3.14
A |
B |
C |
D |
Y |
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
|
|
|
|
|
Group the terms as follows:
(8)(9): A B C D A B C D A B C
(10)(11): A B C D A B C D A B C
(12) (14): A B C D A B C D A B D
Combine the simplified groups and apply techniques of Boolean algebra to simplify further:
Y A B C A B C A B D
A B(C C) A B D
A B A B D
A(B B D)A(B D)A B A D
Figure 3.38 Shows the logic diagram of the simplified expression.
A
B
Y AB AD
D
FIGURE 3.38
Example 3.14
Simplified SOP Circuit
SECTION 3.4 REVIEW PROBLEM
3.5 Find the maximum SOP and POS simplifications for the function represented by
Table 3.11. |
|
|
