
Digital design with CPLD applications and VHDL (R. Dueck, 2000)
.pdf
70 C H A P T E R 3 • Boolean Algebra and Combinational Logic
Let’s reexamine Table 3.4. To find the sum-of-products expression for Y, we wrote a minterm for each line where Y 1. To find the SOP expression for Y, we must write a minterm for each line where Y 0. Variables A, B, and C must appear in each minterm, in true or complement form. A variable is in complement form (with a bar over the top) if its value is 0 in that minterm, and it is in true form (no bar) if its value is 1.
We get the following minterms for Y:
A B CA B C
A B C A B C
A B C
Thus, the SOP form of Y is
Y A B C A B C A B C A B C A B C
To get Y in POS form, we must invert both sides of the above expression and apply De-
Morgan’s theorems to the righthand side.
Y Y A B C A B C A B C A B C A B C
(A B C)(A B C)(A B C)(A B C)(A B C)
(A B C)(A B C)(A B C)(A B C)(A B C)
This Boolean expression can be implemented by the logic circuit in Figure 3.20.
We don’t have to go through the whole process outlined above every time we want to find the POS form of a function. We can find it directly from the truth table, following the
FIGURE 3.20
Logic Circuit for Y (A B C) (A B C)(A B C) (A B C)(A B C)
procedure summarized below. Use this procedure to find the POS form of the expression given by Table 3.4. The terms in this expression are the same as those derived by DeMorgan’s theorem.

3.2 • Sum-of-Products and Product-of-Sums Forms |
71 |
N O T E
Deriving a POS expression from a truth table:
1.Every line on the truth table that has a LOW output corresponds to a maxterm in the truth table’s Boolean expression.
2.Write all truth table variables for every maxterm in true or complement form. If a variable is 1, write it in complement form (with a bar over it); if it is 0, write it in true form (no bar).
3.Combine all maxterms in an AND function.
Note that these steps are all opposite to those used to find the SOP form of the Boolean expression.
EXAMPLE 3.8 |
Find the Boolean expression, in both SOP and POS forms, for the logic function repre- |
||||||||
|
sented by Table 3.7. Draw the logic circuit for each form. |
||||||||
|
|
Table 3.7 Truth Table for Example 3.8 (with minterms |
|||||||
|
|
and maxterms) |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
A |
B |
C |
D |
Y |
Minterms |
Maxterms |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
1 |
A B C D |
|
|
|
|
0 |
0 |
0 |
1 |
1 |
A B C D |
A B C D |
||
|
0 |
0 |
1 |
0 |
0 |
A B C D |
|||
|
0 |
0 |
1 |
1 |
1 |
A B C D |
|||
|
0 |
1 |
0 |
0 |
0 |
|
|||
|
0 |
1 |
0 |
1 |
0 |
|
A B C D |
||
|
0 |
1 |
1 |
0 |
0 |
|
A B C D |
||
|
0 |
1 |
1 |
1 |
0 |
A B C D |
A B C D |
||
|
1 |
0 |
0 |
0 |
1 |
A B C D |
|||
|
1 |
0 |
0 |
1 |
0 |
A B C D |
|||
|
1 |
0 |
1 |
0 |
1 |
A B C D |
|||
|
1 0 |
1 |
1 |
0 |
A B C D |
||||
|
1 1 |
0 |
0 |
1 |
|
|
|||
|
1 |
1 |
0 |
1 |
1 |
A B C D |
|
|
|
|
1 |
1 |
1 |
0 |
1 |
A B C D |
A B C D |
||
|
1 1 |
1 |
1 |
0 |
|
||||
|
|
|
|
|
|
|
|
|
|
Solution All minterms (for SOP form) and maxterms (for POS form) are shown in the last two columns of Table 3.5.
Boolean Expressions:
SOP form:
Y A B C D A B C D A B C D A B C D A B C D A B C DA B C D A B C D
POS form:
Y (A B C D)(A B C D)(A B C D)(A B C D) (A B C D)(A B C D)(A B C D)
(A B C D)
The logic circuits are shown in Figures 3.21 and 3.22.
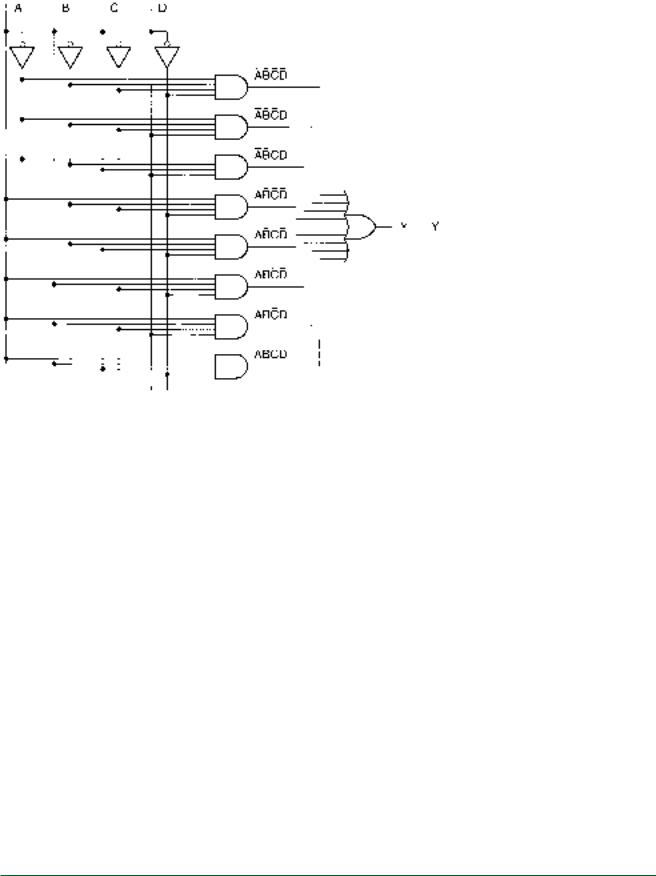
72 C H A P T E R 3 • Boolean Algebra and Combinational Logic
FIGURE 3.21
Example 3.8
SOP Form
FIGURE 3.22
Example 3.8
POS Form

3.3 • Theorems of Boolean Algebra |
73 |
SECTION 3.2 REVIEW PROBLEM
3.3Find the SOP and POS forms of the Boolean functions represented by the following truth tables.
a. A |
B |
C |
|
Y |
b. A |
B |
C |
Y |
||
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
1 |
||
0 |
0 |
1 |
|
0 |
0 |
0 |
1 |
0 |
||
0 |
1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
||
0 |
1 |
1 |
|
0 |
0 |
1 |
1 |
0 |
||
1 |
0 |
0 |
|
1 |
1 |
0 |
0 |
1 |
||
1 |
0 |
1 |
|
1 |
1 |
0 |
1 |
1 |
||
1 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
||
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
0 |
||
3.3 Theorems of Boolean Algebra
The main reason to learn Boolean algebra is to learn how to minimize the number of logic gates in a network. Boolean expressions with many terms, such as those represented by the logic diagrams in Figures 3.21 and 3.22, are seldom in their simplest form. It is often possible to apply some techniques of Boolean algebra to derive a simpler form of expression that requires fewer gates to implement.
For example, the logic circuit in Figure 3.21 requires eight 4-input AND gates and an 8-input OR gate. Using Boolean algebra, we can reduce its Boolean expression to Y AD A B C A B D A B C. This form can be implemented with 4 AND gates and a 4-input OR. You will use a simplification technique for this example in an end-of- chapter problem. In the meantime, let us examine some basic rules of Boolean algebra.
Commutative, Associative, and Distributive Properties
K E Y T E R M S
Commutative property A mathematical operation is commutative if it can be applied to its operands in any order without affecting the result. For example, addition is commutative (a b b a), but subtraction is not (a b b a).
Associative property A mathematical function is associative if its operands can be grouped in any order without affecting the result. For example, addition is associative ((a b) c a (b c)), but subtraction is not ((a b) c a (b c)).
Distributive property Full name: distributive property of multiplication over addition. The property that allows us to distribute (“multiply through”) an AND across several OR functions. For example, a(b c) ab ac.
AND and OR functions are both commutative and associative. The commutative property states that AND and OR operations are independent of input order. For inputs x and y,
Theorem 1: xy yx
and
Theorem 2: x y y x
The associative property allows us to perform several two-input AND or OR functions in any order. In other words,
Theorem 3: (xy)z x(yz) (xz)y
and
Theorem 4: (x y) z x (y z) (x z) y
74 C H A P T E R 3 • Boolean Algebra and Combinational Logic
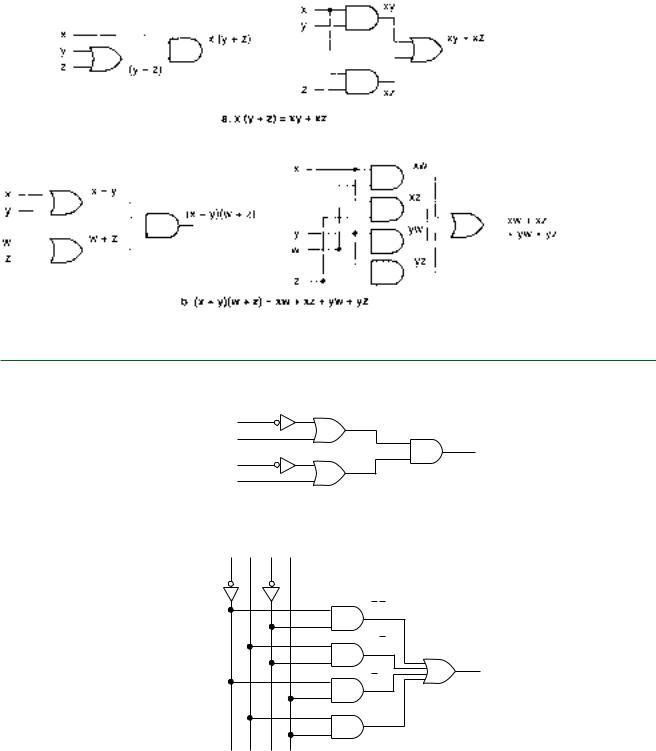
The distributive property allows us to “multiply through” an AND function across several OR functions. For example,
Theorem 5: x(y z) xy xz
and
Theorem 6: (x y)(w z) xw xz yw yz
Figure 3.23 shows the logic gate equivalents of these theorems.
FIGURE 3.23
Distributive Properties
EXAMPLE 3.9
FIGURE 3.24
Example 3.9
Distributive Property
Find the Boolean expression of the POS circuit in Figure 3.24a. Apply the distributive property to transform the circuit to an SOP form.
A
B
Y
C
D
|
|
|
a. POS form |
A |
B |
C |
D |
|
|
|
AC |
|
|
|
BC |
|
|
|
Y |
|
|
|
AD |
|
|
|
BD |
b. SOP form

3.3 • Theorems of Boolean Algebra |
75 |
Solution The Boolean expression for Figure 3.24a is Y (A B)(C D). Using the distributive property, we get the expression Y A C BC AD BD. The logic diagram for this expression is shown in Figure 3.24b.
In Example 3.9, we see that the distributive property can be used to convert a POS circuit to SOP or vice versa. In this case, the circuit was not simplified, just transformed.
EXAMPLE 3.10
FIGURE 3.25
Example 3.10
Distributive Property
Write the Boolean expression for the circuit in Figure 3.25a. Use the distributive property to convert this to an SOP circuit.
A
B
C |
|
D |
Y |
|
E
F
a. POS form
A B C D E F
ABCE
ABCF
Y
ABDE
ABDF
b. SOP form
Solution The Boolean expression for Figure 3.25a is AB(C D)(E F). The distributive property can be applied in two stages:
Y (ABC ABD)(E F)
ABCE ABCF ABDE ABDF
The logic diagram for this equation is shown in Figure 3.25b. This results in a network that is “wider” (more gates on one level), but also “flatter” (fewer levels). The advantage of the second circuit is that signals would pass through the network faster, since it has fewer
levels of gating. |
|
|
Single-Variable Theorems
There are thirteen theorems that can be used to manipulate a single variable in a Boolean expression. An easy way to remember these theorems is to divide them into three groups:
1.Six theorems: x AND/OR/XOR 0/1
2.Six theorems: x AND/OR/XOR x/ x
3.One theorem: Double Inversion
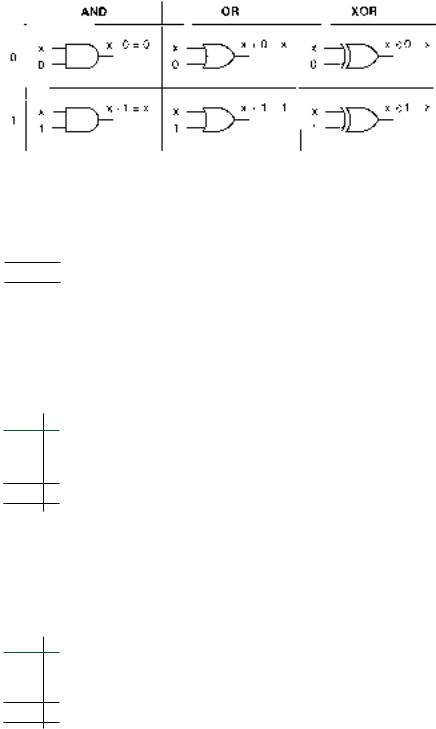
76 C H A P T E R 3 • Boolean Algebra and Combinational Logic
x AND/OR/XOR 0/1
The theorems in the first group can be generated by asking what happens when x, a Boolean variable or expression, is at one input of an AND, an OR, or an XOR gate and a 0 or a 1 is at the other.
Examine the truth table of the gate in question. Hold one input of the gate constant and find the effect of the other on the output. This is the same procedure we used in Chapter 2 to examine the enable/inhibit properties of logic gates.
Each of these six theorems can be represented by a logic gate, as shown in Figure 3.26.
FIGURE 3.26
X AND/OR/XOR 0/1
x 0:
A |
x |
Y |
|
|
|
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
If x 0, Y 0
If x 1, Y 0
(Can never have both inputs HIGH, therefore output is always LOW.)
Theorem 7: x 0 0
x 0:
A x Y
0 0 0
0 1 1
1 0 1
1 1 1
If x 0, Y 0
If x 1, Y 1
(LOW input enables OR gate.)
Theorem 8: x 0 x
x 0:
A x Y
0 0 0
0 1 1
1 0 1
1 1 0

3.3 • Theorems of Boolean Algebra |
77 |
If x 0, Y 0
If x 1, Y 1
(XOR acts as a noninverting buffer.)
Theorem 9: x 0 x
x 1:
A x Y
0 0 0
0 1 0
1 0 0
1 1 1
If x 0, Y 0
If x 1, Y 1
(HIGH input enables AND gate.)
Theorem 10: x 1 x
x 1:
A x Y
0 0 0
0 1 1
1 0 1
1 1 1
If x 0, Y 1
If x 1, Y 1
(One input always HIGH, therefore output is always HIGH.)
Theorem 11: x 1 1
x 1:
A x Y
0 0 0
0 1 1
1 0 1
1 1 0
If x 0, Y 1
If x 1, Y 0
(XOR acts as an inverting buffer.)
Theorem 12 x 1 x
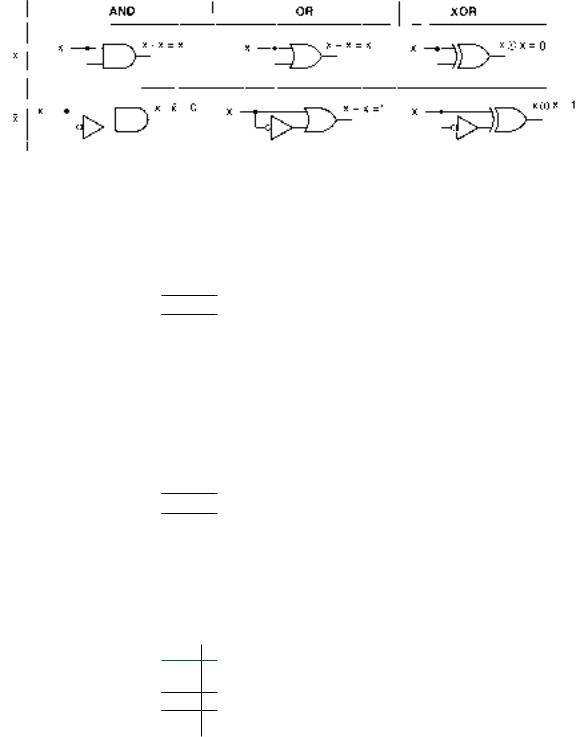
x AND/OR/XOR x/ x
Six theorems are generated by combining a Boolean variable or expression, x, with itself or its complement in an AND, an OR, or an XOR function.
Again, we can use the AND, OR, and XOR truth tables. For the first three theorems, we look only at the lines where both inputs are the same. For the other three, we use the lines where the inputs are different.
78 C H A P T E R 3 • Boolean Algebra and Combinational Logic
Figure 3.27 shows the logic gates that represent these theorems.
FIGURE 3.27
X AND/OR/XOR X/X
x x:
A |
x |
Y |
|
|
|
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
If x 0, Y 0
If x 1, Y 1
Theorem 13: x x x
x x:
A |
x |
Y |
|
|
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
If x 0, Y 0
If x 1, Y 1
Theorem 14: x x x
x x:
A x Y
0 0 0
0 1 1
1 0 1
1 1 0
If x 0, Y 0
If x 1, Y 0
(Output is LOW if neither input is HIGH or if both are.)
Theorem 15: x x 0

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.3 • Theorems of Boolean Algebra |
79 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x x: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
x |
|
|
|
Y |
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
If x 0, Y 0 |
|
||||||||||
|
|
|
|
|
|
|
If x 1, Y 0 |
|
||||||||||
|
|
|
|
|
|
|
(Since inputs are opposite, can never have both HIGH. Output always LOW.) |
|
||||||||||
|
|
|
|
|
|
|
Theorem 16: |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
x x 0 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x x: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
x |
|
|
Y |
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
If x 0, Y 1 |
|
||||||||||
|
|
|
|
|
|
|
If x 1, Y 1 |
|
||||||||||
|
|
|
|
|
|
|
(Since inputs are opposite, one input always HIGH. Therefore, output is always HIGH.) |
|||||||||||
|
|
|
|
|
|
|
Theorem 17: |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
x x 1 |
|
||||||||
|
|
|
|
|
|
|
x x: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
x |
|
|
Y |
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
If x 0, Y 1 |
|
||||||||||
|
|
|
|
|
|
|
If x 1, Y 1 |
|
||||||||||
|
|
|
|
|
|
|
(One input HIGH, but not both.) |
|
||||||||||
|
|
|
|
|
|
|
Theorem 18: |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
x x 1 |
|
||||||||
|
|
|
|
|
|
|
Double Inversion |
|
||||||||||
|
|
|
|
|
|
|
The final single-variable theorem is just common sense. It states that a variable or expres- |
|||||||||||
|
x |
|
|
|
x |
sion inverted twice is the same as the original variable or expression. It is given by: |
|
|||||||||||
|
|
|
|
|
||||||||||||||
|
x |
x |
|
|||||||||||||||
|
|
|
|
|
|
|
Theorem 19: |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
x x |
|
||||||||
FIGURE 3.28 |
|
|
|
|
|
This theorem is illustrated by the two inverters in Figure 3.28. |
|
|||||||||||
Double Inversion |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Multivariable Theorems
There are numerous multivariable theorems we could learn, but we will look only at five of the most useful.
