Текст

Для определения усилий рассмотрим произвольное сечение k с координата-

ми xk и yk и углом наклона к горизонту φk (рис. 2.28, б), образованному каса-

тельной t к оси арки в сечении k.

На основании общих правил определения усилий в произвольном сечении

Эти выражения представляют собой соответственно изгибающий момент и

поперечную силу в сечении k простой балки.

Подставляя (2.16) в (2.13)… (2.15), получим выражения для усилий в произ-

Выражения (2.17 … 2.19) свидетельствуют о том, что эпюры усилий в трёх-

шарнирных арках криволинейны.

Применение записанных формул для расчёта арки рассмотрим на конкрет-

ном примере.

Пример 2.7. Требуется построить эпюры усилий для трёхшарнирной арки,

изображённой на рис. 2.29, а. Ось арки очерчена по квадратной параболе

с началом координат в левой опорной точке арки.

Решение. 1. Определим геометрические характеристики расчётных сечений ар-

ки.

71

Примем шаг расчётных сечений арки x = 3 м.

Координаты расчётных сечений при принятом шаге определяются по выше-

приведённому уравнению параболы.

Углы наклона касательных в расчётных сечениях определяем по их тангенсу

Тогда необходимые для применения формул (2.18) и (2.19) значения триго-

нометрических функций могут быть вычислены по зависимостям

cos jk =1/(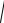1+ tg2jk ; sin jk = tgjk ×cos jk .

Необходимые для расчёта значения координат и тригонометрических функ-

ций для рассматриваемой арки представлены в табл. 2.2.

Таблица 2.2

Геометрические характеристики сечений трёхшарнирной арки из примера 2.7

72

73

2. Определим вертикальные опорные реакции

∑MA = 0; 20·12·6 + 60·12 + 60·18 – VB·24 = 0, VB = 135 кН.

∑MB = 0; VA·24 – 20 ·12·18 – 60 ·12 – 60 ·9 = 0, VA = 225 кН.

3.Построим эпюры Qб и Mб (рис. 2.29, а) и определим балочные усилия для каждого расчётного сечения.

4.Определим распор в арке по формуле (2.12)

H = 1260/4 = 315 кН.

5. Определяем усилия в сечениях арки по формулам (2.17) … (2.19).

При ручном счёте процесс вычисления усилий удобно проводить в таб-

личной форме. Для рассматриваемой арки данные расчёта приведены в табл. 2.2. По данным таблицы построены эпюры M, Q и N для арки (рис. 2.29, б).

2.5.4. Сравнительный анализ работы трехшарнирной арки и балки

Как видно из формул определения усилий в сечениях арки (2.17) … (2.19)

по сравнению с простой балкой арка обладает определёнными преимущест-

вами. При одинаковых пролётах и нагрузках в сечениях арки изгибающие моменты меньше, чем в простой балке. Следовательно, при прочих равных условиях поперечные сечения арки будут меньшими, и конструкция в целом может более экономичной по расходу материалов. В трёхшарнирных арках существенное уменьшение изгибающих моментов имеет место в средней части пролёта, где в балках, как правило, изгибающие моменты достигают наибольших значений. Поперечные силы в сечениях арки также меньше, чем в простой балке. Меньшие изгибающие моменты и поперечные силы в арках обусловлены наличием распора. В то же время наличие распора приводит к появлению в сечениях арки продольных сжимающих сил. Как показала прак-

тика большинство строительных конструкционных материалов, арка лучше работает на сжатие, нежели на изгиб.

74

2.5.5. Понятие о рациональном очертании оси трехшарнирной системы

Так как большинство строительных конструкционных материалов лучше работает на сжатие, чем на изгиб, очевидно, что наиболее экономичными с точки зрения работы материала будут трехшарнирные системы, где изги-

бающие моменты малы или равны нулю. В этом случае говорят о рациональ-

ном очертании оси трехшарнирной системы.

Выражение (2.17) позволяет представить пределы правомерности поста-

новки такой задачи при действии на трехшарнирную систему вертикальной нагрузки и установить аналогию для ее решения. Если потребовать равенства нулю изгибающего момента в произвольном сечении трехшарнирной систе-

мы, представив последний в форме (2.17), получим уравнение:

M kб – H· yk = 0.

Решая это уравнение относительно, получим зависимость

уk = M kб ,

H

которая устанавливает для произвольного сечения трехшарнирной системы взаимно однозначное соответствие между ординатой M kб балочной эпюры моментов и ординатой сечения yk. Поскольку никаких ограничений (см. под-

разд. 2.5.3) на положение произвольного сечения при выводе (2.17) установ-

лено не было, полученная зависимость представляет всю совокупность сече-

ний трехшарнирной системы. Следовательно, можно записать:

На основании (2.20) можно утверждать, что очертание оси трехшарнирной системы, в сечениях которой отсутствуют изгибающие моменты, подобно очертанию балочной эпюры моментов.

В качестве примера рассмотрим трёхшарнирную арку, загруженную рав-

номерно распределённой нагрузкой (рис.2.30).

75

В этом случае опорные реакции арки будут равны

Для произвольного сечения арки с координатами (x, y) запишем выраже-

Приравняв полученное выражение нулю, после несложных преобразова-

ний получим уравнение квадратной параболы

Следовательно, в параболической арке при действии равномерно распре-

делённой нагрузки во всех сечениях арки изгибающие моменты равны нулю,

т.е. для данного вида нагрузки параболическое очертание оси арки является рациональным. При вертикальной нагрузке все сечения такой арки работают только на сжатие.

Аналогично можно показать, что при действии радиальной равномерно распределённой нагрузки, рациональным будет круговое очертание арки.

В общем случае, рациональное очертание трехшарнирной системы, как зависящее от вида действующей нагрузки, может быть и более сложным и содержать как криволинейные участки оси, так и ломаные.

Таким образом, чтобы получить рациональное очертание трехшарнирной системы или трёхшарнирной системы для заданного вида нагрузки, доста-

точно построить эпюру изгибающих моментов Mб, все её ординаты разделить на величину распора H, и «перевернуть» полученную кривую или ломаную линию (рис.2. 31).

76

2.6. Статически определимые плоские и пространственные фермы

2.6.1. Общие положения. Классификация ферм

Фермой называется стержневая система, остающаяся геометрически не-

изменяемой, если в ней все жёсткие узлы заменить шарнирными.

Хотя узлы в действительных конструкциях жёсткие, возможность их за-

мены в расчётных схемах на шарнирные объясняется тем, что в фермах, осо-

бенно металлических, размеры поперечных сечений стержней существенно меньше их длины. Поэтому напряжения в элементах конструкции, вызванные изгибом, значительно меньше напряжений от растяжения (сжатия), и ими можно пренебречь.

Для того чтобы шарнирно – стержневая расчётная схема фермы достаточ-

но точно отражала действительную работу её элементов, кроме допущения о замене жёстких узлов шарнирными, вводится допущение об узловой переда-

че нагрузки на фермы.

Таким образом, фермы являются наиболее обширным классом расчётных схем, элементы которых работают в условиях одноосного напряжённого со-

стояния (растяжения – сжатия).

В зависимости от характера структуры и направления действия нагрузок фермы, как и все расчётные схемы, разделяются на плоские (см. рис.1.12, к – п) и пространственные (см. рис.1.13, а – в).

В плоской ферме (рис. 2.32) стержни, ограничивающие контур фермы сверху, образуют в совокупности верхний пояс, снизу – нижний пояс. Эле-

менты, связывающие между собой пояса фермы, образуют решётку фермы,

которая содержит вертикальные стержни – стойки и наклонные - раскосы.

В зависимости от наклона раскосов от опоры к центру фермы их разделяют на восходящие и нисходящие.

77

Расстояние d между узлами фермы в пределах поясов принято называть

панелью, наибольшее расстояние между поясами h – высотой, расстояние между центрами опорных узлов l– пролётом фермы.

Плоские фермы классифицируются по следующим признакам:

1. По типу опорных закреплений и направлению опорных реакций, вы-

зываемых вертикальной нагрузкой фермы разделяют на балочные (см.

рис.1.12, к – м и рис. 2.32) и распорные (см. рис. 1.12, н, о). Балочные фермы могут быть бесконсольные (см. рис. 1.12, к – м), консольно – балочные (рис. 2.33, а) и консольные (рис. 2.33, б).

2. По очертанию поясов фермы могут быть с параллельными поясами

(см. рис.1.12, к и рис. 2.32), треугольные (см. рис. 1.12, д), трапецеидальные

(см. рис.1.12, м), с полигональными поясами. Полигональным может быть как один из поясов фермы (рис. 2.33, в и г), так и оба (рис. 2.33, д). В зависимости от очертания полигонального пояса фермы могут быть параболическими, эл-

липтическими, круговыми.

3.По типу решётки фермы называются раскосными (см. рис. 1.12, к – м

ирис. 2.32, 2.33, в)), с треугольной решёткой (рис. 2.33, а и г), полураскос-

ными (рис. 2.33, д), многораскосными (рис. 2.33, е) и многорешётчатыми

(рис. 2.33, ж).

Необходимое условие геометрической неизменяемости ферм проверяется по условию (1.6), которое для статически определимых ферм при W = 0 при-

нимает вид

2У – Сф – Соп = 0 .

Обозначая общее число стержней С = Сф + Соп, можем записать

Условие (2.21) помимо кинематического смысла (см. подразд. 1.5.2), име-

ет чётко выраженный статический смысл. При вырезании какого – либо узла фермы, получают систему сходящихся сил, состоящую из внешних сил, при-

ложенных к узлу фермы, и продольных внутренних сил (усилий) каждого подходящего к узлу стержня. Для плоской системы сходящихся сил можно

78

составить два уравнения равновесия (см. табл. 2.1, п. 2). Таким образом, ве-

личина 2У в (2.21) – это количество уравнений равновесия, которое можно составить для всех узлов фермы, а С – число реакций и усилий, подлежащих определению. При равенстве этих величин ферма является статически опре-

делимой.

Анализ геометрической структуры ферм в целях доказательства достаточ-

ности условия (1.6) был показан в подразд. 1.5.2. Следует отметить, что, если ферма имеет решётку, образованную по способу “ триады” ( раскосную или треугольную), условие (2.21) является необходимым и достаточным, и они в таких случая называются простейшими.

Пространственные фермы в основном различаются по структуре образо-

вания. Это могут быть двойные фермы (би – фермы, см. рис. 1.13, а), купола

(см. рис.1.13, в) и башни (см. рис.1.13, б). По очертанию поясов и типу ре-

шётки используется та же система классификации, что и в плоских фермах.

Необходимое условие геометрической неизменяемости ферм проверяется по условию (1.12), которое для статически определимых ферм при W = 0

принимает вид

Условие (2.22) помимо кинематического смысла (подразд. 1.5.3) имеет чётко выраженный статический смысл. При вырезании какого – либо узла фермы, получают систему сходящихся сил, состоящую из внешних сил, при-

ложенных к узлу фермы, и продольных внутренних сил (усилий) каждого подходящего к узлу стержня. Для пространственной системы сходящихся сил можно составить три уравнения равновесия (см. табл. 2.1, п.6).Таким об-

разом, величина 3У в (2.22) выражает количество уравнений равновесия, ко-

торое можно составить для всех узлов фермы, а С – число реакций и усилий,

подлежащих определению. При равенстве этих величин ферма является ста-

тически определимой.

79

Анализ геометрической структуры ферм для доказательства достаточно-

сти условия (1.12) был показан в подразд. 1.5.3.

2.6.2. Способы определения усилий в стержнях плоских ферм

Основной трудностью при расчёте ферм любой структуры и при любых опорных закреплениях является определение реакций в связях. Прежде чем рассчитывать ферму, необходимо проанализировать, как она образована, и

определить к какому типу она относится: к балочной, консольной или рас-

порной. Затем определить реакции во внешних связях и только после этого приступать к определению усилий.

Для определения усилий в стержнях ферм применяются как аналитиче-

ские способы расчета, так и графический. При аналитическом способе расче-

та ферм используются два способа: способ вырезания узлов и способ сече-

ний.

1. Способ вырезания узлов. Как уже отмечалось, при вырезании любого узла фермы мы получаем плоскую систему сходящихся сил, которая должна удовлетворять двум уравнениям равновесия (см. табл. 2.1, п. 2).

При использовании данного способа неизвестные усилия в стержнях фер-

мы, сходящихся в узле, направляют от узла, задаваясь их положительным значением (растяжением). Если в результате расчёта получается отрицатель-

ное значение, значит рассматриваемый стержень сжат.

Последовательность рассмотрения узлов фермы должен быть таков, чтобы каждый последующий узел содержал не более двух неизвестных усилий.

При этом может оказаться, что в некоторых стержнях фермы усилия рав-

ны нулю (нулевые стержни) или их достаточно просто определить, не выре-

зая узел. Для этого рассмотрим некоторые частные случаи равновесия узлов

ферм.

1. Двухстержневой незагруженный узел (рис. 2.34, а). Проектируем все силы на оси n1 и n2, перпендикулярные осям стержней.

80