Текст

и вычисление интеграла можно выполнить, применив способ «перемноже-

ния» эпюр, обычно называемый способом Верещагина.

Для использования этого способа необходимо, чтобы одна из эпюр выра-

жения (4.30) была прямолинейной. Это условие в данном случае выполняется всегда, так как эпюра Mk вспомогательного состояния состоит только из пря-

молинейных участков.

Рассмотрим существо способа Верещагина. На рис. 4.9 показаны участки двух эпюр изгибающих моментов Mk и MF. Приняв за начало координат точ-

ку пересечения прямой, ограничивающей эпюру Mk, с осью абсцисс, выразим ординату этой эпюры через произвольную координату x:

Mk = x tg α.

Тогда интеграл, входящий в (12.26) можно записать в виде:

∫ Mk MF dx = ∫ xtgαMF dx = tgα∫ xMF dx .

Из рис.4.9 видно, что MF dx – элементарная площадка dP эпюры MF, а

произведение x·MF dx = xdP – элементарный статический момент этой пло-

щадки относительно вертикальной оси.

Следовательно,

∫ xMF dx = S = Ωx0 ,

l

где S – статический момент площади P эпюры MF, относительно вертикаль-

ной оси; x0 – координата центра тяжести этой площади.

Тогда

Итак, если одна из перемножаемых эпюр ограничена прямой, а другая

имеет произвольное очертание, то ∫ M k M F dx можно вычислить как произ-

l

ведение площади эпюры произвольного очертания P на ординату под её центром тяжести y0 , взятую из прямолинейной эпюры.

Основные особенности применения способа Верещагина (см. 4.33):

171

1. Произведение P· y0 считается положительным, если площадь P и ор-

дината y0 расположены по одну сторону оси стержня, т.е. имеют одинаковые знаки, и отрицательным, если они расположены по разные стороны оси.

2. Эпюра, по которой определяется площадь P, может быть любого очер-

тания, но эпюра, по которой берётся ордината y0, может быть только прямо-

линейной.

3. Если обе эпюры прямолинейные, то безразлично, по какой из них оп-

ределяется площадь P, а по какой – ордината y0.

4. Когда одна из эпюр имеет сложное очертание, её представляют как геометрическую сумму простых фигур, для которых известны их площади и координаты центра тяжести (табл. 4.1). Тогда формула (4.30) для рассматри-

ваемого участка стержня запишется как

∫ Mk MF dx = W1 × y01 + W2 × y02 + W3 × y03 +..... + Wn × y0n .

l

Недостатком способа Верещагина, при всей его наглядности и простоте,

является громоздкость вычислений при сложных очертаниях эпюр усилий.

Потому в инженерной практике часто используют готовые формулы «пере-

множения» эпюр, которые выведены на основе способа Верещагина.

Наиболее распространёнными из таких формул являются следующие: 1. Формула «перемножения» трапеций (рис.4.10).

где: h = 0,5(a + b); f = 0,5(c + d) ± ql2/8 (знак ± зависит от того, в какую сто-

рону направлена выпуклость кривой на эпюре MF).

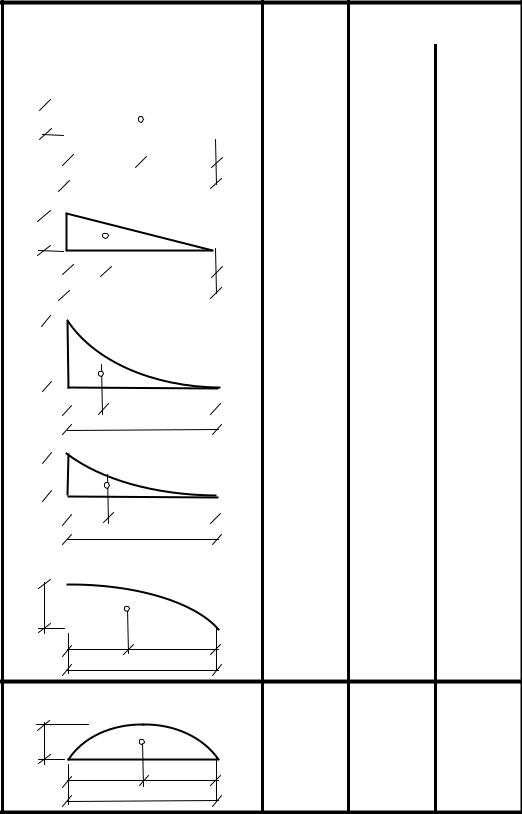
Таблица 4.1

Пощади и центры тяжести простейших геометрических фигур

172

a b

l

Квадратная

парабола

a b

l

Формулы (4.34) и (4.35) справедливы при любых значениях показанных на рис. 4.10 и 4.11 ординат. Формула (4.35) применима в случае, если эпюра

MF очерчена по квадратной параболе, а при очертании по кубической пара-

боле она является приближённой.

173

Правило знаков для формул (4.34) и (4.35): произведение ординат, входя-

щих в формулы положительное, если ординаты в обеих эпюрах отложены

по одну сторону от оси стержня, и отрицательное – если по разные сторо-

ны.

Для сравнения покажем на простом примере применение способа Вереща-

гина и формулы Симпсона.

Пример 4.1. Требуется определить прогиб средней точки пролёта простой балки с консолью (рис.4.12, а), загруженной равномерно распределённой на-

грузкой q = 8 кН/м в пролёте и силой F = 16 кН на консоли.

В силу простоты рассматриваемого примера опустим определение опор-

ных реакций в балке при действии внешней нагрузки (грузовое состояние) и

при действии единичной силы, приложенной по направлению искомого пе-

ремещения (вспомогательное состояние) Эпюры изгибающих моментов для

этих состояний приведены на рис.4.12, б.

Решение. 1. Используем способ Верещагина, для этого эпюру MF пред-

ставим как сумму пяти простейших геометрических фигур, расположенных

на двух участках (рис.4.12, в), и напротив центров тяжести каждой из этих фигур подсчитать ординаты y0 на эпюре M1.

Согласно табл.4.1 эти площади и ординаты будут следующими:

174

2. Выполним вычисление по формуле Симпсона (4.35), для чего в середи-

не каждого участка подсчитаем ординаты эпюр MF и M1(рис.4.12, г):

Как видно из приведённого примера, объём вычислений при использова-

нии формулы (4.35) значительно меньше, чем при использовании способа Верещагина.

Пример 4.2. Требуется для балки, приведенной на рис.4.13, а, определить угол поворота сечения, примыкающего к опоре K, линейные перемещения узлов расчётной схемы и построить её деформированную схему.

Решение. Целью данного примера является изучение техники определения перемещений, поэтому при рассмотрении расчётных схем всех ниже приве-

дённых состояний опущены части расчёта, содержащие определение опор-

ных реакций и построение эпюр усилий изгибающих моментов. На рис.4.13

приведены расчётные схемы всех состояний, величины опорных реакций и необходимые эпюры изгибающих моментов.

Перемножение эпюр производится по участкам между узлами A, B, C, D и K (см. рис.4.13, а).

1. Определим угол поворота сечения, примыкающего к опоре K (рис.4.13,

б). В рассматриваемом вспомогательном состоянии для определения угла поворота в сечении K прикладываем единичный момент.

В соответствии с (4.32)

175

498

+ 0,5·72·3·1} = EI рад.

Участок DK

В данном выражении для участка AB «перемножение» эпюр выполнено по (4.34); для участка BC – по (4.33); для участка CD – по (4.35); для участка

DK – по (4.33);

Поскольку общий множитель для всего интеграла – 1/ EI, а на участках AB

и CD заданная жёсткость равна 2EI, то записи перемножений эпюр по этим

участкам разделены на число 2 (учёт соотношения жёсткостей).

2. Определим горизонтальное перемещение узлов A и B ( рис.4.13, в).

В рассматриваемом вспомогательном состоянии для определения пере-

мещения прикладываем горизонтальную единичную силу. Поскольку при из-

гибе мы пренебрегаем продольными деформациями и считаем, что вдоль оси стержня между его концами отсутствуют смещения, то безразлично, где при-

Участок DK

В данном выражении для участка AB «перемножение» эпюр отсутствует,

так как в эпюре M2 на этом участке нет изгибающих моментов; для участка

BC «перемножение» эпюр выполнено по (4.33); для участка CD – по (4.35);

для участка DK – по (4.34). Для участков AB и CD учтено соотношение жё-

сткостей.

Искомое перемещение получили со знаком минус, т.е. перемещение на-

правлено в сторону, противоположную направлению приложенной единич-

ной силы.

176

3. Аналогичным образом определяем ещё два перемещения, используя

вспомогательные состояния, показанные на рис.4.13 г и д:

4. На основании определённых перемещений узлов и эпюры изгибающих моментов грузового соcтояния MF (см. рис.4.13, а) строим деформирован-

ную схему (рис. 4.13, е).

Данная схема является условной, так как построить в одном масштабе са-

му расчётную схему и её перемещения невозможно из-за малости последних по сравнению с размерами конструкции.

При построении деформированной схемы кроме учета ранее сформули-

рованных допущений о нерастяжимости и несжимаемости изгибаемых стержней, необходимо принять еще одно допущение: жёсткие узлы расчёт-

ной схемы не деформируются.

Таким образом, отложив в выбранном масштабе определённые нами пе-

ремещения узлов и представив изгиб стержней по эпюре изгибающих момен-

тов MF, получим изображение условной деформированной схемы заданной конструкции.

Пример 4.3. Требуется определить прогиб консоли рамы, показанной на рис.4.14, а, стойка и ригель которой изготовлены из двутавра № 24 (Iz = 3460

см4), подкос AB – из трубы d = 102 мм и толщиной стенки t = 3 мм (A = 9,3 см2).

177

Грузовое состояние рамы, соответствующая ему эпюра MF и значение продольной силы NF в подкосе показаны на рис. 4.14, а, а вспомогательное состояние, соответствующая ему эпюра M1 и продольная сила N1 – на рис.4.14, б.

Решение. 1. Определим жесткости стержней рамы:

∙на изгиб (стойка и ригель) EI = 2,06·108·3460·10-8 = 7 127,6 кН·м2;

∙продольная жесткость (подкос AB) EA=2,06·108·9,3·10-4=19,16·104 кН.

2.Определим прогиб консоли по формуле (4.30).

Пример 4.4. Требуется определить изменение угла между левой стойкой и центральным раскосом фермы, изображённой на рис. 4.15, а. Пояса фермы изготовлены из двух неравнополочных ∟80 х 50 х 6 (A1 = = 2·7,55 = 15,1 см2),

а решётка – из двух равнополочных уголков ∟50 х 5 (A2 = 2·4,8 = 9,6 см2).

Грузовое состояние фермы и соответствующая ему эпюра NF показаны на рис. 4.15, а, а вспомогательное состояние и соответствующая ему эпюра N1

– на рис.4.15, б.

Во вспомогательном состоянии для определения изменения угла между двумя сечениями приложены противоположно направленные единичные мо-

менты. Так как в стержнях фермы при действии внешней нагрузки действуют только продольные силы, действия единичных моментов во вспомогатель-

ном состоянии заменяется действиями пар с плечами, равными длинам стержней, углы поворота которых подлежат определению. Силы пар прило-

жены в узлах фермы по концам этих стержней.

178

Решение. 1. Определим жёсткости стержней фермы:

∙пояса EA1 = 2,06·108·15,1·10-4 = 31,106·104 кН = EA;

∙решётки EA1 = 2,06·108·9,6·10-4 = 19,776·104 кН = 0,636EA.

2.Определим искомое перемещение по формуле (4.28):

откуда, подставив численное значение жёсткости EA, получим

4.5.2. Перемещения от теплового воздействия

При тепловом воздействии любой материал изменяет свою форму. Поэто-

му необходимо различать деформации от силового и теплового воздействий.

При силовом воздействии на плоские расчётные схемы имеют место изгиб и растяжение (сжатие) (рис.4.16. а). При тепловом воздействии имеют место искривление и удлинение (укорочение) (рис.4.16, б). Причем последние виды деформаций изменяют только форму элемента, но не вызывают никаких на-

пряжений в расчётных сечениях статически определимых систем.

При расчёте на тепловое воздействие учитывается не температура окру-

жающей среды, а её ожидаемое изменение в процессе эксплуатации соору-

жения.

В целях упрощения инженерных расчётов вводится допущение о линей-

ном характере изменения температуры по высоте сечения элемента. Зная расположение нейтральной оси стержня, можно заданное изменение темпе-

ратуры разложить на два воздействия – на равномерный и неравномерный нагрев (рис. 4.17).

Равномерный нагрев характеризуется температурой t0,ºС на уровне ней-

тральной оси n – n и вызывает только удлинение или укорочение стержня.

При этом температура на уровне нейтральной оси в общем случае равна

179

Неравномерный нагрев характеризуется перепадом температур t, вызы-

вающей искривление стержня из-за различия в удлинении волокон по высоте его сечения.

Рассмотрим деформации бесконечно малого элемента стержня dx

(рис.4.18) при тепловом воздействии отдельно для равномерного и неравно-

мерного нагрева.

При действии равномерного нагрева удлинение (укорочение) бесконечно малого элемента стержня будет равно (рис.4.18, а)

Чтобы получить формулу для определения перемещений от теплового воздействия рассмотрим линейно деформируемую расчётную схему в со-

стоянии теплового воздействия (рис.4.19, а) и вспомогательное состояние k

180