4 .5. Учет временного запаздывания в нелинейной системе

Е

W_л(s)

сли в системе есть нелинейный элемент с запаздыванием, то его структурно представляют в виде собственно нелинейного элемента и звена чистого запаздывания:

x y

Н.Э.

З.Ч.З.

Л.Ч.

Рис. 4.5.1

З.Ч.З. – звено чистого запаздывания.

(4.5.1)

(4.5.2)

(4.5.3)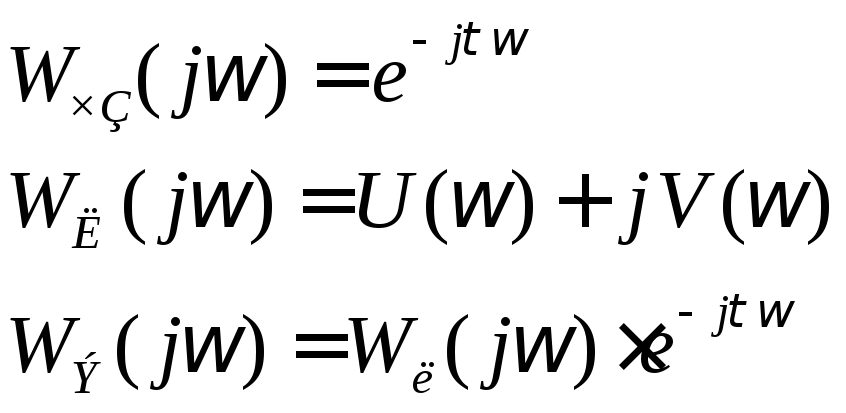

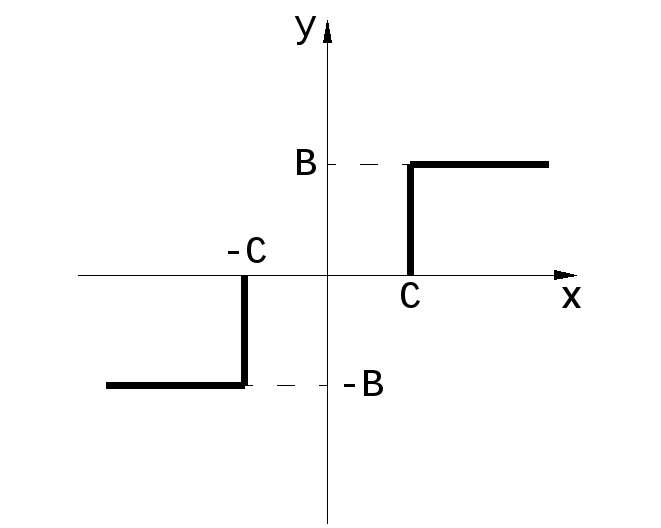
Выражение 4.5.3. представляет собой АФХ линейной части с запаздыванием.

Н.Э. возьмём в виде в виде идеального трёхпозиционного реле ( рис. 4.5.2), с эквивалентной ПФ

Рис. 4.5.2

(4.5.4)

П



(_k)

-z(A)

ω_кр

Рис. 4.5.3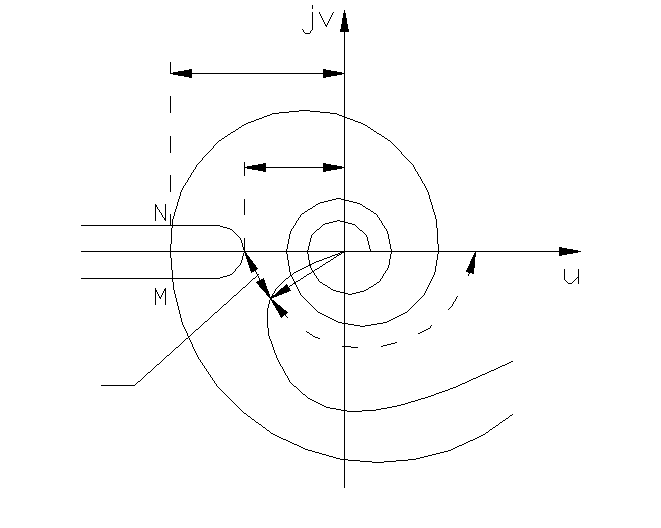

остроим кривые :W_л(jω), W_э(jω), -z(A)= -1/J(A).

W_э(j)

W_л(j)



K

_k_k

Для исследования автоколебаний характеристические уравнения систем с запаздыванием и без него представим в виде

; (4.5.5)

Если годографы W_э(jω) и -z(A) пересекаются, то имеются автоколебания. При достаточно малом запаздывании кривые не пересекутся и автоколебаний не будет. Критическое время τ_к запаздывания можно найти без построения годографа W_э(jω), а только по кривым W_л(jω) и

-z(A), что гораздо проще. Поскольку в критическом случае кривая W_э(jω) проходит через крайнюю правую точку кривой -z(A), то можно записать равенство . Из этого выражения можно найти критическую частоту ω_к. Учитывая, что в этой точке фазовый сдвиг равен –π, то из выражения ,найдем τ_к

.

• е

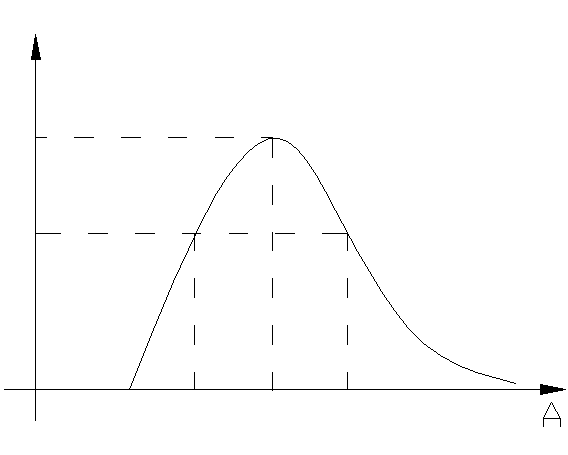
  J(A)

  сли<_k – автоколебаний нет

• е

  

  

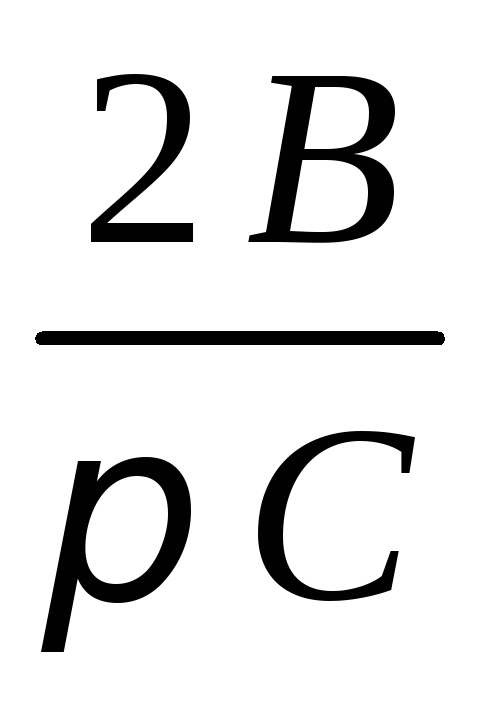
  сли>_k – возможны два периодических режима с одной частотой и разными амплитудами.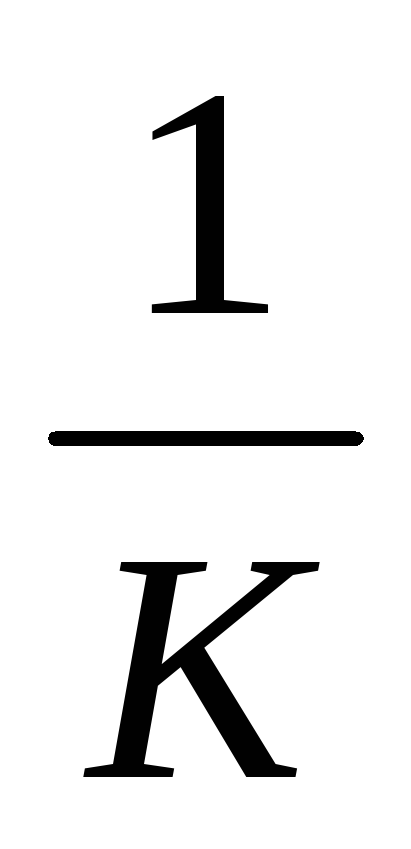

Д

С А_M А_N

Рис.4. 5.4

ля определения амплитуд колебаний на графике кривойJ(A) отложим отрезок 1/К из (рис.4.5.3). Из этого же рисунка , согласно критерия устойчивости автоолебаний следует, что колебания с амплитудой А_M неустойчивы, а с большей амплитудой A_N- устойчивы. Общий вывод: нелинейная система устойчива в «малом» и автоколебательна в «большом». Для исключения автоколебаний временное запаздывание по возможности нужно уменьшать, а зону нечувствительности увеличивать до величины допустимой статической точностью системы.

0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000

6. Л

   

   огарифмический критерий устойчивости систем. Определение

Автоколебательных режимов.

J(A)

W(j)

g x y

После гармонической линеаризации характеристическое уравнение имеет вид:

. (4.6.1)

Преобразуем его к виду

. (4.6.2)

АФХ линейной части и НЭ имеют вид:

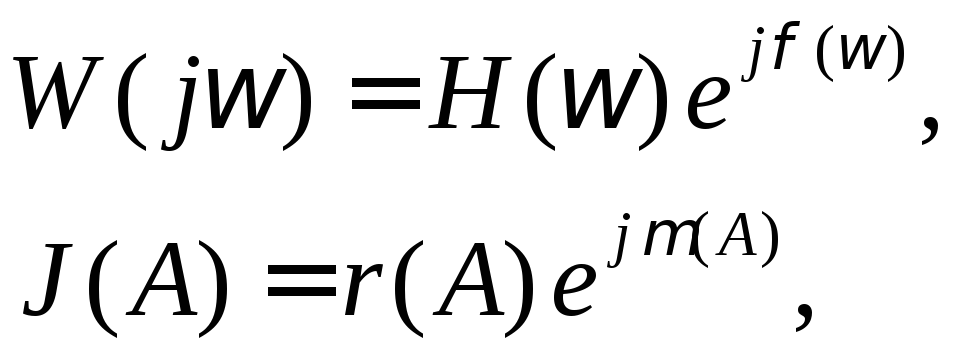(4.6.3)

Учитывая, что в соответствии с формулой Эйлера

,

выражение (4.6.2) можно записать в виде

(4.6.4)

Приравнивая в правой и левой частях значения модулей и аргументов, получим

уравнение гармонического баланса фаз и амплитуд:

(4.6.5)

Для перехода к логарифмической форме запишем:

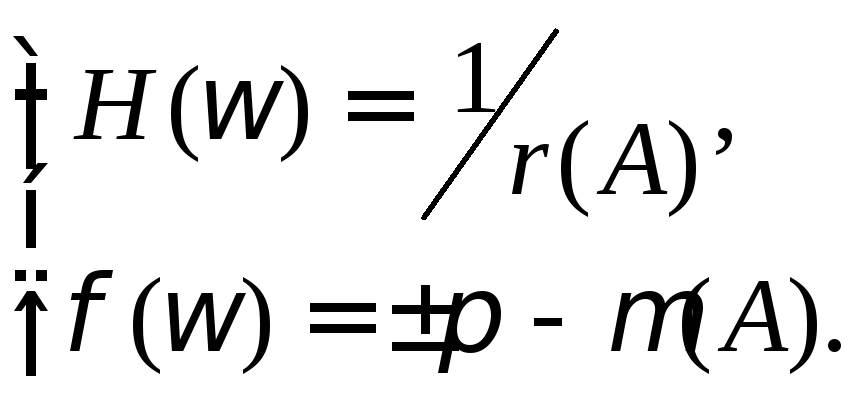(4.6.6)

В логарифмическом виде

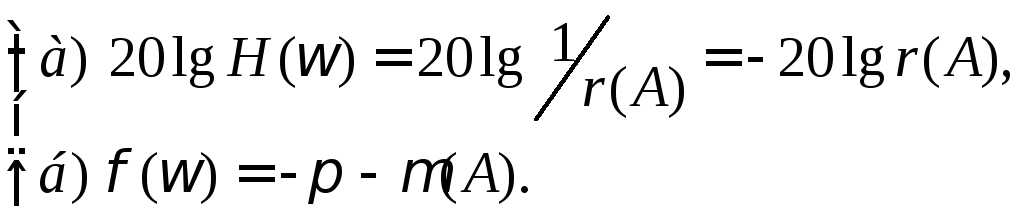(4.6.7)

Выражение (4.6.7) показывает, что при одновременном выполнении условий а) и б) в САУ возможны автоколебания. Одновременность выполнения уравнений а) и б) состоит в том, что точки пересечения логарифмических амплитудных характеристик 20lgH(ω) – линейной части и 20lg(1/r(A)) – нелинейного элемента должны лежать на одной вертикали с точками пересечения фазовых характеристик – линейной частии– нелинейного элемента .

С помощью графического решения уравнений (4.6.7) можно найти частоту и амплитуду автоколебаний. При этом возможны два метода.

М



етод шаблонов

Шаблоны приведены, например, в ( Атлас по ТАУ, под ред Ю.И.Топчеева).

Рассмотрим применение метода на примере линейной части с ПФ

,(4.6.8)

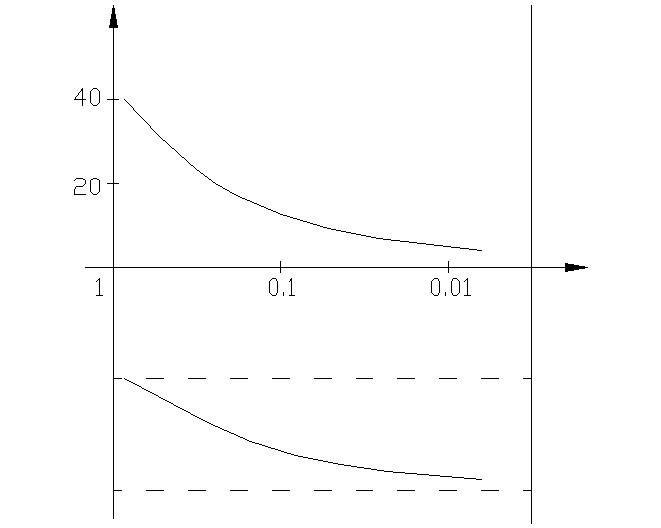
и НЭ типа – люфт (рис. 4.6.1б). Шаблон люфта имеет вид (рис.4.6.1а):

Д

ля люфта.

Рис. 4.6.1 б

Рис. 4.6.1 а

Рис. 54а

Рис. 55а

Шаблон строится в том же масштабе, что и ЛЧХ линейной части. Затем шаблон накладывается на ЛЧХ линейной части так, чтобы совпали оси абсцисс и, затем, перемещается вдоль оси частот и при этом определяется точка пересечения и , и ,лежащие на одной вертикали.

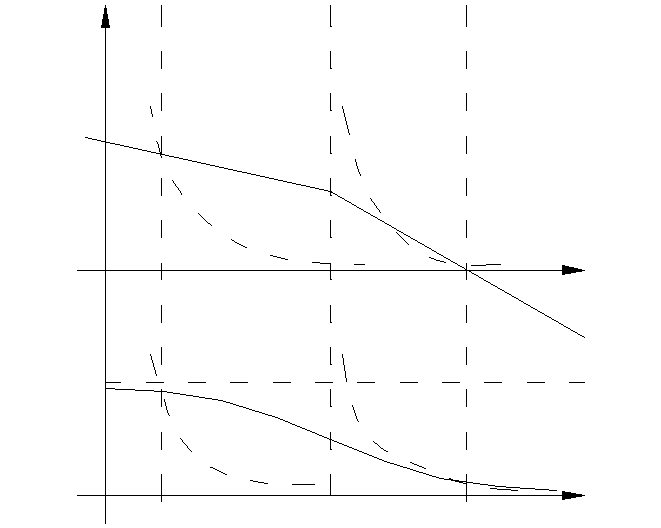
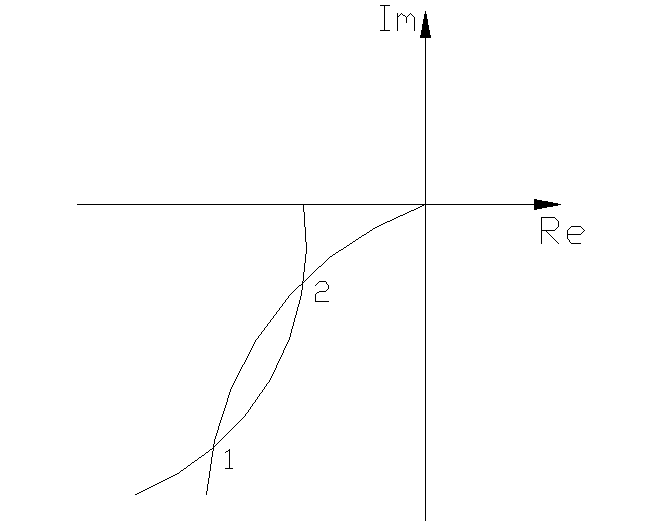
Если точки пересечения амплитудных и фазовых характеристик находятся на одной вертикали, то автоколебания системы возможны, если нет, то в системе нет автоколебаний. Из рис. 4.6.2а видно, что возможны два случая подобной ситуации. Для вывода критерия определения устойчивости автоколебаний по логарифмическим характеристикам рассмотрим комплексную плоскость (рис.4.6.2б), на которой построены годограф АФХ W(jω) линейной части и годограф нелинейного элемента. Наблюдаем также две точки пересечения. В соответствии с критерием устойчивости автоколебаний делаем вывод, что в т.1 колебания неустойчивые, а в т.2-устойчивые. В т.2 амплитуда и частота колебаний больше значений соответствующих переменных в т.1.

Анализируя рис.4.6.2а, можно сформулировать следующий критерий.

Для определения устойчивости автоколебаний в системе с неоднозначным нелинейным элементом необходимо дать приращение амплитуде колебаний.

Если с ростом амплитуды, точка пересечения амплитудных характеристик и, лежащая на одной вертикали с точкой пересечения фазовых характеристик и , перейдёт в область над ЛАХ 20lgH(ω), то колебания устойчивы, а если в область под ЛАХ 20lgH(ω) – то неустойчивы.

₁

₂



Рис. 4.6.2 a

Рис. 4.6.2 б

В соответствии с критерием частоте ω₂ соответствуют колебания устойчивые; а частоте ω₁ – неустойчивые.