4 .4. Частотный метод определения автоколебательных режимов и их устойчивости (метод Гольдфарба л.С.)

Этот метод графоаналитический и представляет собой применение метода гармонической линеаризации к исследованию устойчивости нелинейных систем на основе частотных характеристик (с использованием критерия Найквиста).

Линейная часть (рис.4.3.1)описывается ПФ: .

Уравнение Н.Э y=F(x). При x=Asinωt , После гармонической линеаризации получим: ,

где эквивалентная ПФ НЭ

,

коэффициенты гармонической линеаризации

ωt=φ.

Характеристическое уравнение замкнутой линеаризованной системы имеет вид:

,(4.4.2)

или

. (4.4.3)

Обычно характеристики нелинейного элемента представляют в нормированном виде:

, . (4.4.4)

где N- коэффициент, учитывающий параметры нелинейной характеристики.

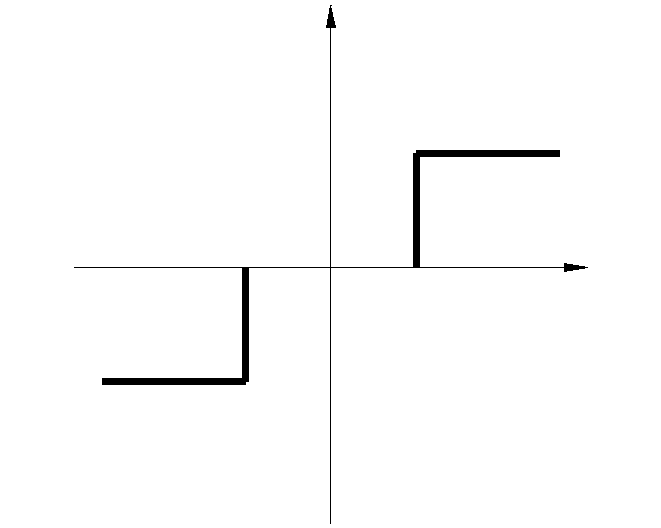
Например, рассмотрим характеристики идеального трёхпозиционного реле (рис.4.4.1, 4.4.2).

Рис. 4.4.1

С

-С

В

-В

y(x)

x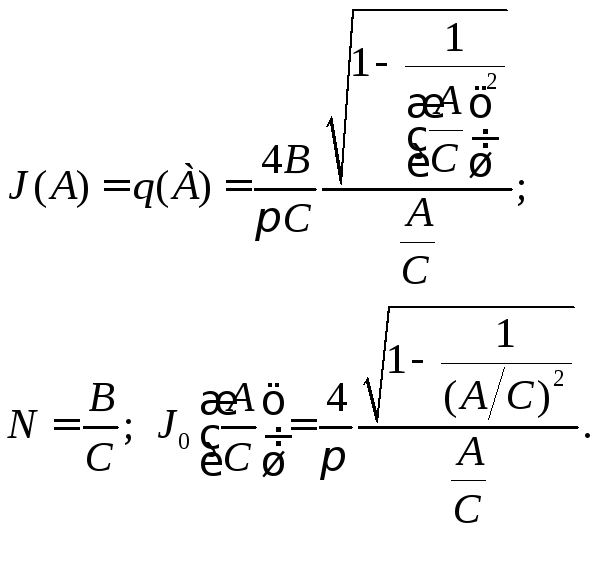

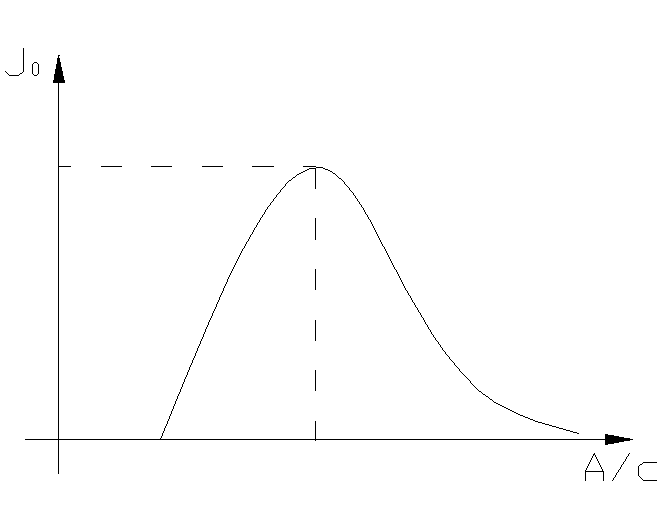
На комплексной плоскости годограф представляет прямую линию на действительной оси т.к.. ПосколькуJ₀(А/С) имеет нелинейный вид (рис.4.4.1), то годограф удобнее представлять в виде (рис.4.4.2).

π/2

А/С→∞

2/π

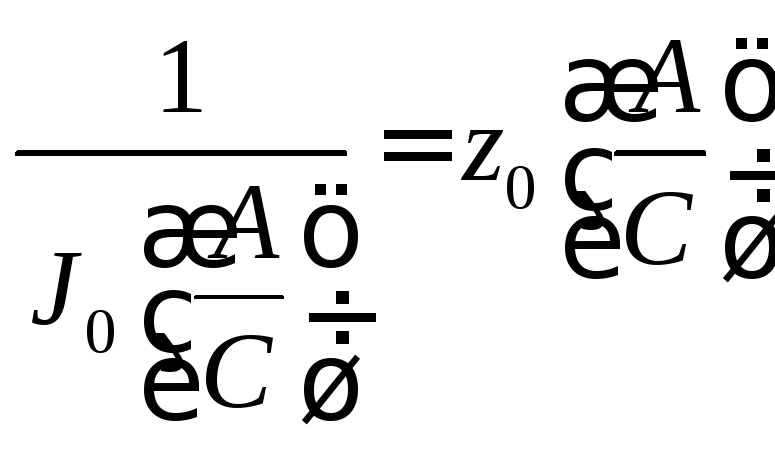(4.4.5)

А/С→1

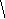
Рис. 4.4.2

Характеристическое уравнение в случае нормированной характеристики имеет вид:

, (4.4.6)

коэффициент N – обычно относят к линейной части.

Для определения автоколебательных режимов характеристическое уравнение (4.4.2) или (4.4.6)

представляют в виде:

а)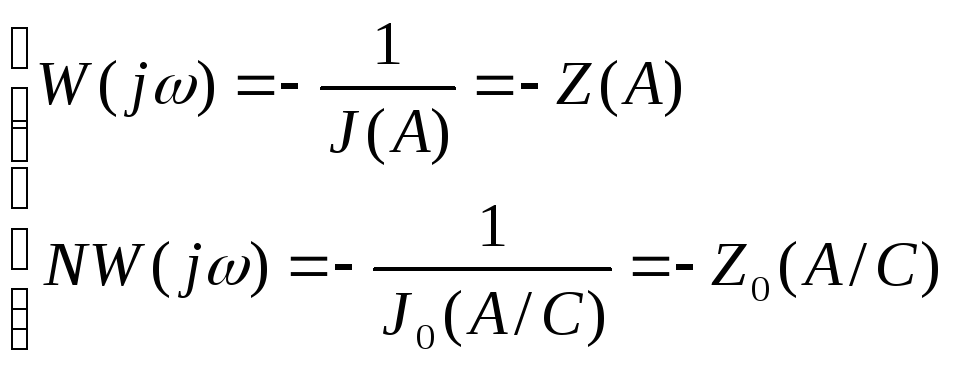б)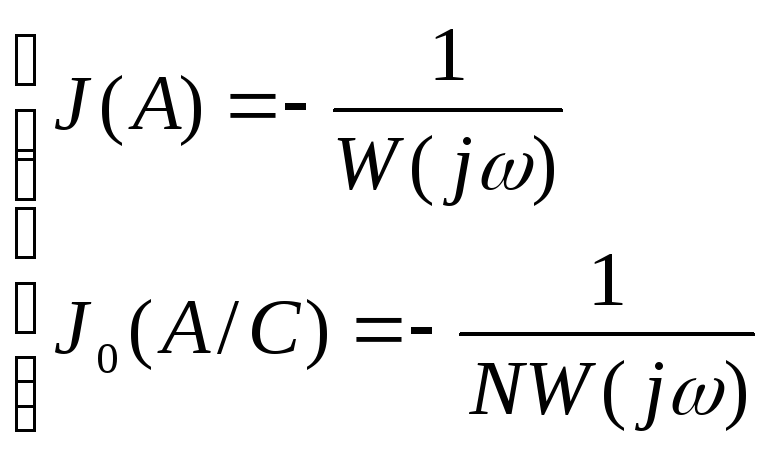(4.4.7)

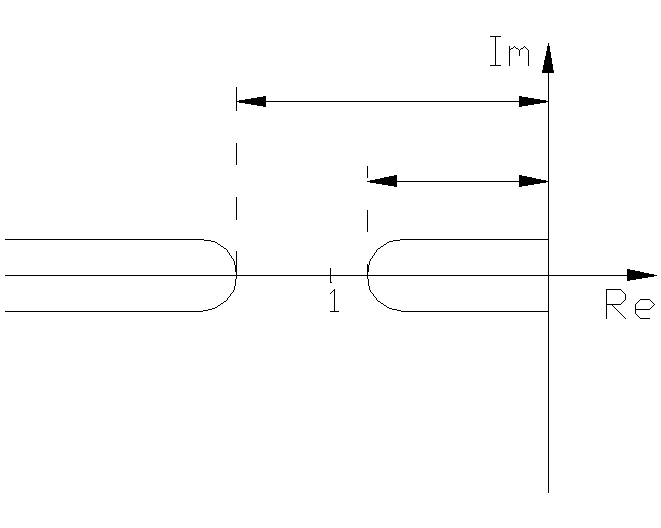
В соответствии с выражением (4.4.7а) на комплексной плоскости строят два годографа:

- АФХ линейной части W(jω) и годограф обратной амплитудной характеристики нелинейного элемента: –Z(A);

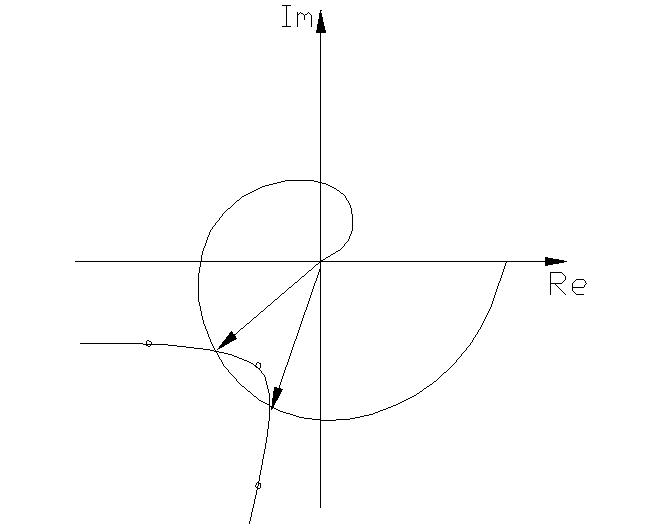-в случае нормированных нелинейных характеристикNW(jω) и –Z₀(A/C).

Е

K₂

K₁

K

L

L₂

-Z(A)

сли эти годографы и или и ) пересекаются, то, следовательно, существуют действительные значения амплитуды A и частоты , удовлетворяющие характеристическому уравнению(4.4.2), и в системе возникают периодические режимы.

Если годографы не пересекаются, то

Рис. 4.4.3 автоколебаний в системе нет.

В

K₁

L₂

K

L

Рис. 44

Рис. 45

данном случае (рис.4.4.3) годографы пересекаются в двух точкахK и L. В них возможны периодические режимы. Определение устойчивости автоколебаний в данном методе производят путем анализа устойчивости систем с помощью критерия Найквиста.

ПФ разомкнутой линеаризованной системы обозначим через:

(4.4.8)

и построим годограф этой функции (рис.4.4.4)

По критерию Найквиста, согласно линейной теории, система находится на границе устойчивости (в ней возникают незатухающий периодический режим), если годограф АФХ W_э(jω,A) проходит через точку с координатами (-1, j0).

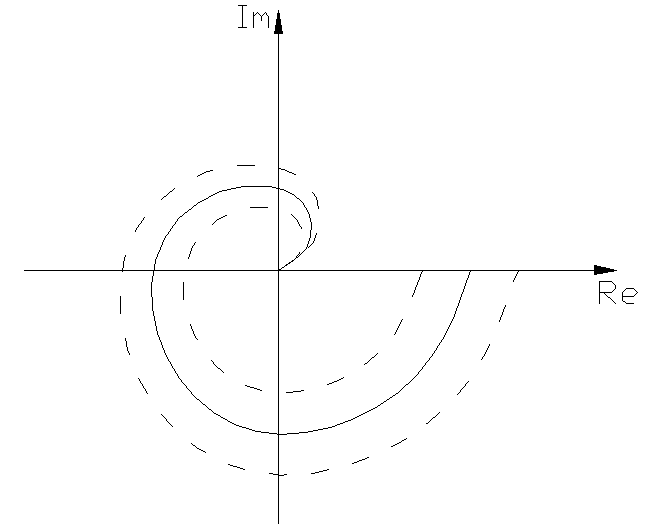
W_э(jω,A+ΔA),А>0, система устойчива

-1

W_э(jω,A-ΔA),А>0, система неуст-ва

W_э(j,А)

Рис.4.4.4

Дадим увеличение амплитуде (А+ΔА). Построим годограф функции W_э(jω, A+ΔA), он не охватывает точку (–1; j0), значит, система по Найквисту устойчива, в устойчивой системе амплитуда колебаний уменьшается, следовательно, годограф АФХ вернется в исходное состояние.

Уменьшим амплитуду колебаний (А–ΔА). Годограф АФХ в этом случае охватывает точку (–1; j0), следовательно, система становится неустойчивой по Найквисту, а в не устойчивой системе амплитуда колебаний увеличивается, и годограф АФХ вернется в исходное состояние.

Таким образом, при изменении амплитуды колебаний в ту или иную сторону годограф АФХ (W_э(jω, A+ΔA)) возвращается в исходное состояние, что и свидетельствует об устойчивости периодического режима или автоколебаний в данной точке.

Т.о. условие устойчивости автоколебаний можно записать в виде:

или (4.4.9)

Вернёмся к рис.4.4.3. Дадим увеличение амплитуде в точке К, (A+A): K₁ . Точка K₁ годографом АФХ линейной части не охватывается, следовательно линеаризованная система устойчива и амплитуда колебаний будет убывать, стремясь к величине А.

Дадим уменьшение амплитуды колебаний (A–A): K₂ Годограф АФХ линейной части охватывает точку K₂, следовательно , система неустойчива, амплитуда колебаний возрастает и стремится к величине А. Поэтому колебания в точке К устойчивы.

Рассмотрим точку L. Рассуждая аналогично получим в этой точке неустойчивый периодический режим или неустойчивые автоколебания.

Оценивая свойства нелинейной системы, можно сделать следующий вывод: система устойчива в «малом» и автоколебательна в «большом».

Пример.

Для иллюстрации возможных ситуаций рассмотрим систему (рис.4.3.1) с нелинейностью (рис. 4.4.5) типа люфт или сухое трение. Рассмотрим различные случаи в зависимости от вида годографа линейной части.

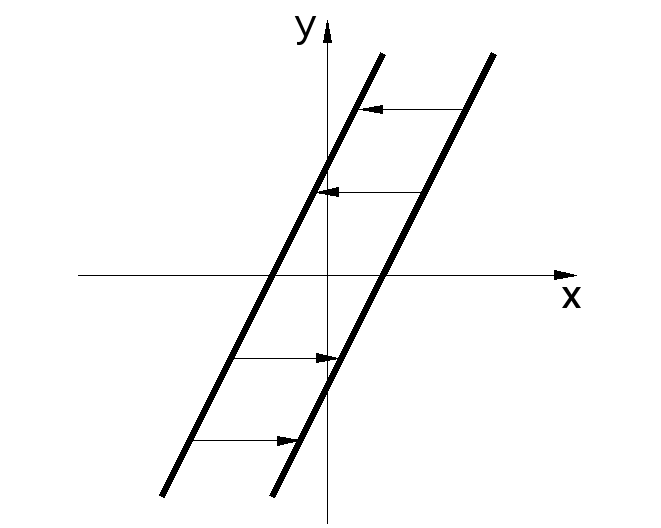
Рис. 4.4.5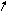

Случай1.

Годографы не пересекаются, следовательно, автоколебаний нет. Вывод: устойчивая линейная система с учетом нелинейности остается устойчивой.

Случай 2.

Cлучай 2. Годографы пересекаются, в точке К- неустойчивый периодический режим. Вывод: неустойчивая линейная система с учетом нелинейности становится устойчивой в «малом» и неустойчивой в «большом».

Случай 3.

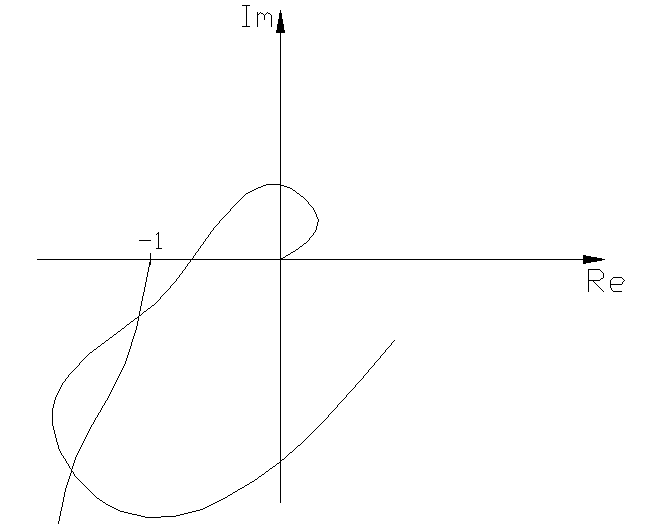
Годографы пересекаются в двух точках.

В

L

точкеK – неустойчивый периодический режим.

В точке L – устойчивые автоколебания.

У

NW(jω)

-Z₀(A/C)

стойчивая линейная система с учетом нелинейности становится устойчивой в «малом» и автоколебательной в «большом».

К

∞

Случай 4.

Линейная часть имеет астатизм второго порядка (=2).

Годографы пересекаются в одной точке, автоколебания устойчивы.

У

W(jω)



стойчивая линейная система с учетом нелинейности становится автоколебательной.

Случай 5.

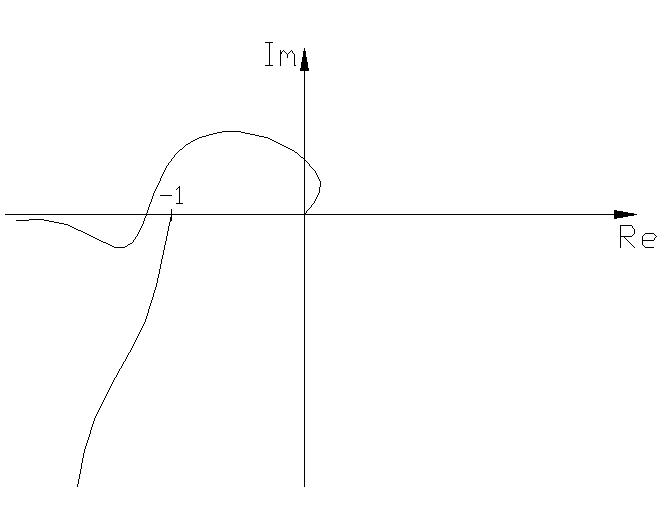
Л



инейная часть имеет астатизм второго порядка (=2).

NW(j)

Г

одографы не пересекаются, автоколебаний нет. Неустойчивая линейная система с учетом нелинейности остается неустойчивой.

.