
- •Теория автоматического управления теория нелинейных автоматических систем
- •Глава1. Виды и особенности нелинейных систем
- •1.1. Типовые нелинейные характеристики
- •1.2. Фазовое пространство и фазовая плоскость
- •1 .3. Типы особых точек и фазовые траектории линейных систем
- •1 .4. Особые линии в нелинейных системах
- •Глава 2. Фазовая плоскость систем, описываемых уравнениями с неаналитической правой частью
- •2 .1. Исследование системы со скользящим режимом
- •2 .2. Исследование релейной системы
- •2 .3. Многолистное фазовое пространство
- •4 .3. Алгебраический метод определения симметричных автоколебаний и их устойчивости
- •4 .4. Частотный метод определения автоколебательных режимов и их устойчивости (метод Гольдфарба л.С.)
- •4 .5. Учет временного запаздывания в нелинейной системе
- •Автоколебательных режимов.
- •2 -Ой метод:
- •4 .7 Несимметричные автоколебания в нелинейных системах.
- •4 .7.1 Гармоническая линеаризация нелинейностей
- •4.7.2 Определение периодических режимов при несимметричных колебаниях
- •6.1. Выбор корректирующих устройств, препятствующих возникновению автоколебаний в нелинейных системах
- •6 .1.1. Выбор линейных последовательных корректирующих устройств
- •(Местных обратных связей)
- •6 .2. Системы с переменной структурой (спс)
- •6.3. Исследование системы с переменной структурой методом фазовой плоскости
- •6 .4. Псевдолинейная коррекция
- •Глава 7. Исследование устойчивости нелинейных систем.
- •7.1. Устойчивость нелинейных систем. Функции Ляпунова а.М.
- •7.2. Теоремы Ляпунова (прямого метода Ляпунова)
- •7.3. Выбор функций Ляпунова
- •7.4. Частотный критерий абсолютной устойчивости
- •7.5. Сравнение методов анализа устойчивости нелинейных систем
- •Глава 8. Исследование устойчивости переходных процессов в нелинейных системах.
- •8.1. Абсолютная устойчивость процессов в нелинейной системе
2 -Ой метод:
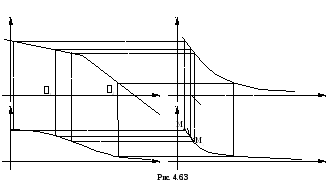
Логарифмические характеристики линейной части и нелинейного элемента строятся раздельно. Причем масштаб по оси ординат должен совпадать, а по оси абсцисс необязательно.
Очевидно, что сразу угадать решение не удастся. Поэтому делают попытки, показанные штриховыми линиями. Последние точки этих пробных прямоугольников М и М1 не попадают на фазовую характеристику нелинейности. Но если они расположены по обе стороны характеристики, как показано на рис. 4.6.3, то решение находится интерполяцией – путем проведения прямой ММ1.
L![]()
![]()
![]()
![]()
![]()
![]()
В
системе с неоднозначной нелинейностью
устойчивые автоколебания возникают в
том случае, если с ростом амплитуды
колебаний
![]() точки пересечения характеристик
точки пересечения характеристик![]() и
и![]() ,
лежащие на одной вертикали с точками
пересечения
,
лежащие на одной вертикали с точками
пересечения
![]() и
и
![]() ,
находятся над ЛАХ линейной части, а если
под ЛАХ линейной части – тогда
автоколебания неустойчивые.
,
находятся над ЛАХ линейной части, а если
под ЛАХ линейной части – тогда
автоколебания неустойчивые.
Для однозначных
линейных характеристик ![]() и, следовательно,
и, следовательно, ![]() .
Уравнение баланса фаз и амплитуд
упрощается:
.
Уравнение баланса фаз и амплитуд
упрощается:
![]() (4.6.9)
(4.6.9)
Автоколебания
возможны только в тех точках, где ФЧХ
линейной части ![]() пересекает линию
пересекает линию ![]() ;
если
;
если ![]() не пересекает линию
не пересекает линию ![]() ,
то автоколебаний нет.
,
то автоколебаний нет.
Решение показано
на рис. 4.6.4, где обозначено: ![]() - ЛАХ линейной части,
- ЛАХ линейной части,
![]() - ЛАХ нелинейного элемента .
- ЛАХ нелинейного элемента .
L(ω) LН(А)
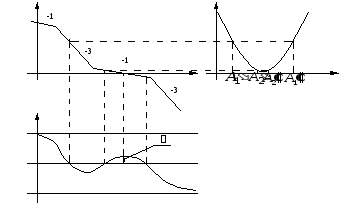



ω1 ω2

Рис. 4.6.4
Согласно
линейной теории система устойчива, так
как имеется запас по фазе γ. Однако на
частотах ω1
и
ω2 выполняются
условия (4.6.9) баланса фаз и амплитуд,
поэтому возможны автоколебания с
амплитудами ![]() .
Для нахождения устойчивых колебаний
перейдем к комплексной плоскости. В
соответствии с критерием получим две
точки неустойчивых колебаний и две
точки устойчивых колебаний.
.
Для нахождения устойчивых колебаний
перейдем к комплексной плоскости. В
соответствии с критерием получим две
точки неустойчивых колебаний и две
точки устойчивых колебаний.
Im Im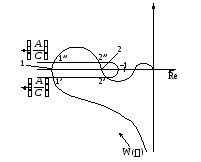
В
точках 1’(ω1,![]() ,
2’’
,
2’’![]() – неустойчивые колебания.
– неустойчивые колебания.
В
точках 1’’![]() ,
2’
,
2’![]() –
устойчивые колебания.
–
устойчивые колебания.
Рис. 4.6.5
автоколебания будут устойчивы, если в точке выполнения баланса фаз и амплитуд дополнительно выполняется условие:
 ,(4.6.10)
,(4.6.10)
т.е. в рассматриваемой точке угловые коэффициенты наклона ЛАХ НЭ и ФЧХ линейной части должны быть разных знаков.
4 .7 Несимметричные автоколебания в нелинейных системах.
4 .7.1 Гармоническая линеаризация нелинейностей
Н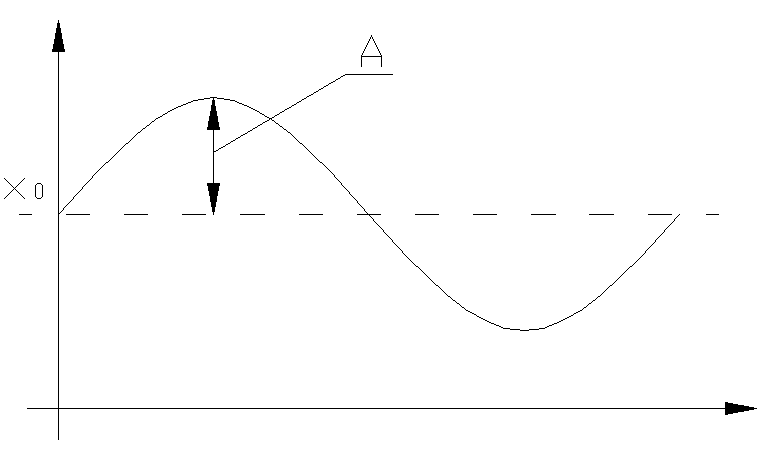 есимметричные
колебания- периодические колебания с
постоянной составляющей (рис.4.7.1)
есимметричные
колебания- периодические колебания с
постоянной составляющей (рис.4.7.1)
В этом случае входная величина х НЭ ищется в виде:
![]() (4.7.1)
(4.7.1)
Рис. 4.7.1
Причин возникновения несимметричных колебаний в общем случае три:
1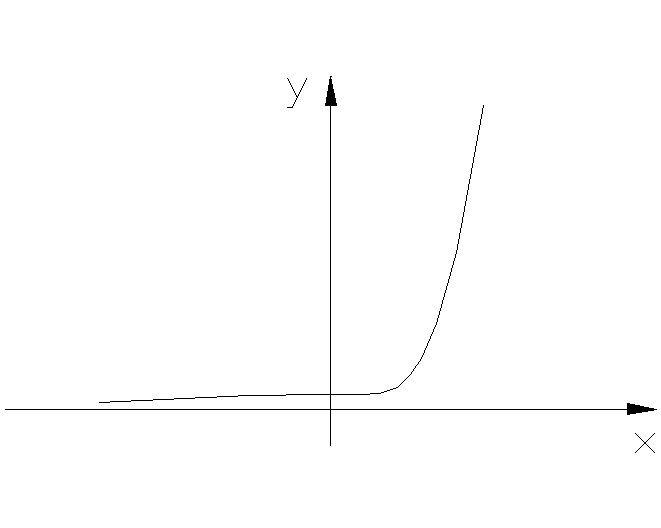 .
Несимметричность нелинейных характеристик;
.
Несимметричность нелинейных характеристик;
Рис. 4.7.2
2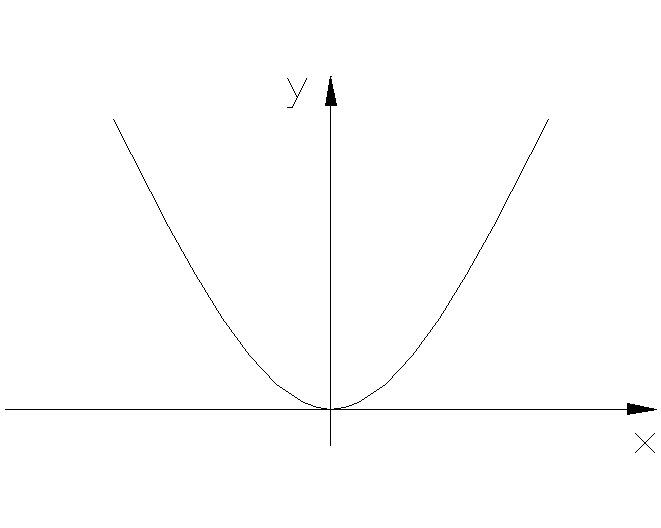 .
Четная симметричность нелинейных
характеристик.
.
Четная симметричность нелинейных
характеристик.
Рис. 4.7.3
3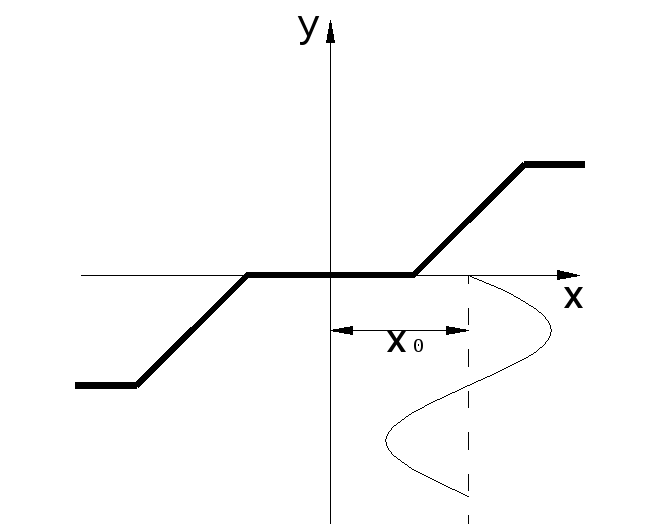 .
Внешнее воздействие с постоянной
составляющей;
.
Внешнее воздействие с постоянной
составляющей;
Рис. 4.7.4
Пусть
нелинейность имеет вид: ![]() . (4.7.2)
. (4.7.2)
Уравнение гармонической линеаризации НЭ принимает вид:
![]() ; (4.7.3)
; (4.7.3)
где коэффициенты гармонической линеаризации определяются по формулам
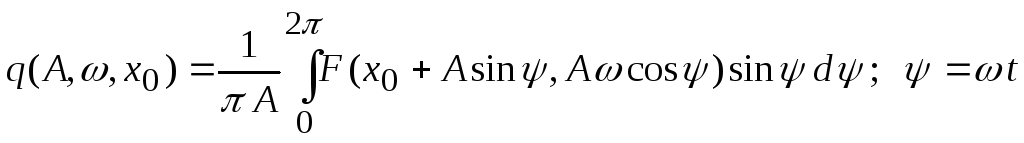 , (4.7.4)
, (4.7.4)
![]() , (4.7.5)
, (4.7.5)
а постоянная составляющая
![]() (4.7.6)
(4.7.6)
где x0 – постоянная составляющая, q и q' – коэффициенты гармонической линеаризации
![]() .
.
В отличии от симметричных колебаний, при несимметричных колебаниях коэффициенты гармонической линеаризации зависят не только от амплитуды и частоты колебаний, но и от постоянного смещения x0.
Вычисление коэффициентов гармонической линеаризации.
Р
1
2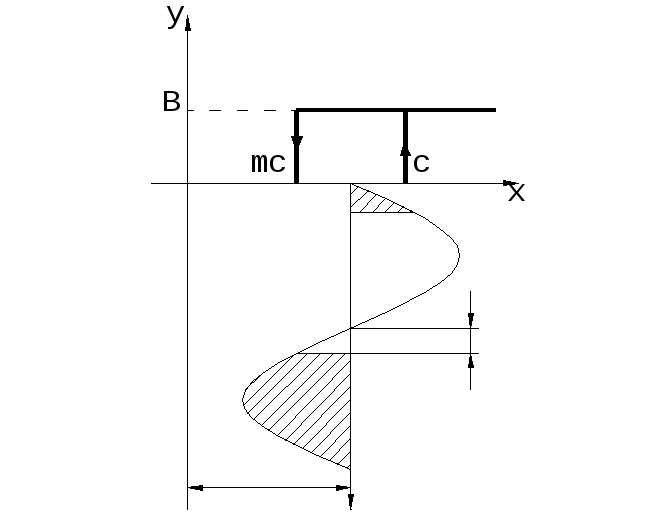
Рассмотрим вычисление постоянной
составляющейограничения: составляющей при ограничениях:
2 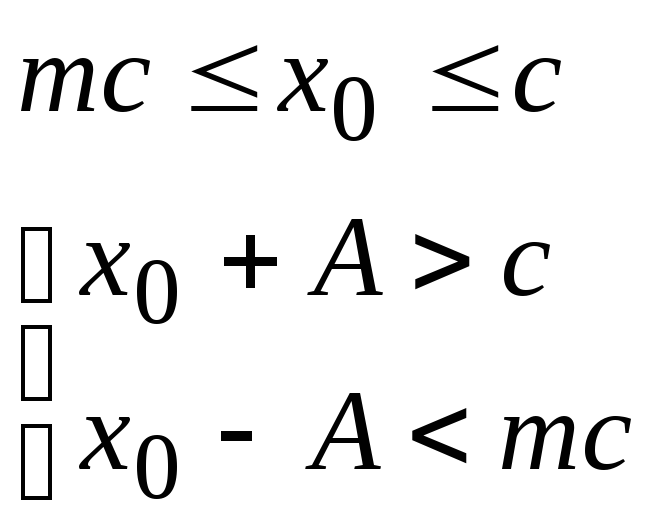 (4.7.7)
(4.7.7)
x0
Рис. 4.7.5
В незаштрихованной области значение у=0.
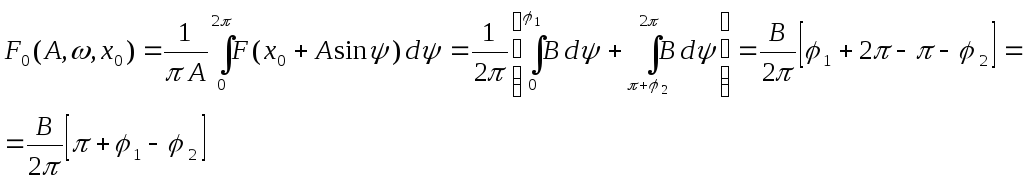 (4.7.8)
(4.7.8)
Выразим значения углов через параметры НЭ и амплитуду А колебаний.
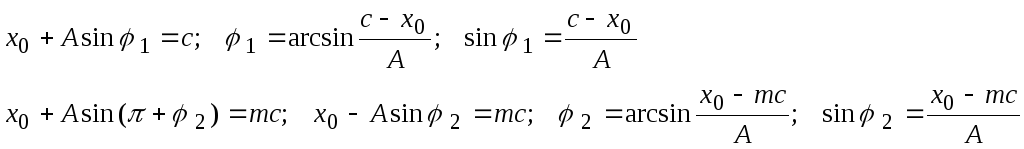 (4.7.9)
(4.7.9)
![]() (4.7.10)
(4.7.10)
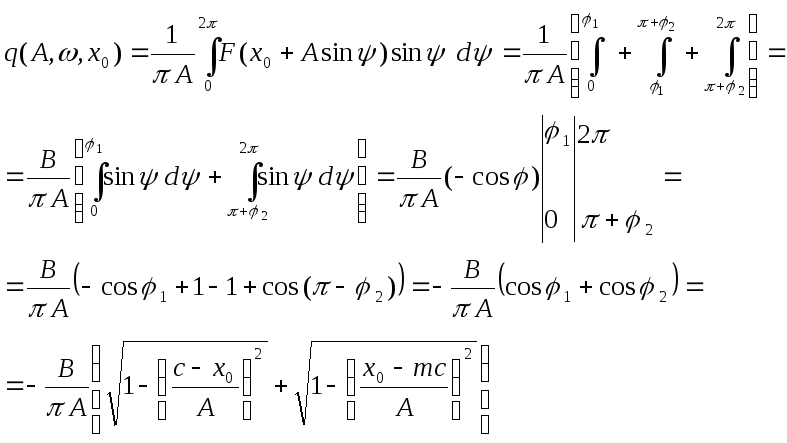 (4.7.11)
(4.7.11)
Это выражение не зависит от частоты.
