1.2. Фазовое пространство и фазовая плоскость

Этот метод применим для систем с уравнениями не более второго порядка.

Переходные процессы, вызванные какими-либо начальными отклонениями координат (при отсутствии внешних воздействий), описываются нелинейными дифференциальными уравнениями динамики в нормальной форме

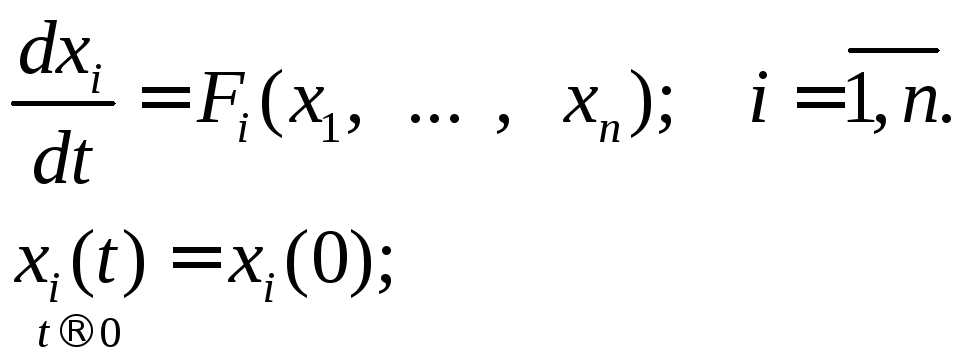(1.2.1)

где x_i – координаты состояния системы, -нелинейные функции.

Если координаты состояния x_i принять за координаты n-мерного пространства, то любой комбинации переменных соответствует определенное состояние или фаза системы, поэтому пространство называют фазовым.

x_3,…, x_n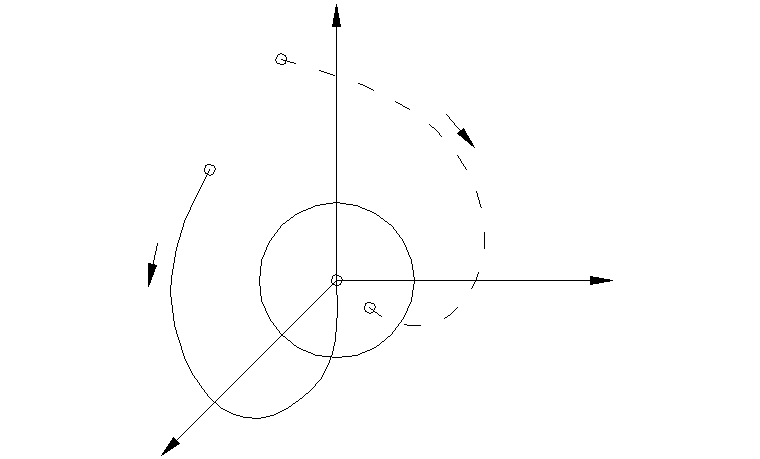

M

ε

x₂

x₁

Рис. 1.2.1

Точку М в n-мерном пространстве, характеризующую действительное (настоящее) состояние системы, называют изображающей. Изменению состояния системы соответствует движение точки по траектории, называемой фазовой. Совокупность фазовых траекторий называют фазовым портретом системы.

Для асимптотически устойчивых систем точка М движется по фазовым траекториям к началу координат.

В случае устойчивых систем точка М движется в область  вокруг начала координат.

По фазовым портретам системы можно судить об устойчивости движения.

Поскольку изображение n-мерного пространства практически невозможно, то наиболее широко распространен метод фазовой плоскости (n=2). Уравнения (1.2.1) при этом имеют вид:

; (1.2.2)

; (1.2.3)

Дифференциальное уравнение фазовых траекторий получим, исключая время из уравнений (1.2.2 и 1.2.3), путём деления уравнения (1.2.3) на уравнение (1.2.2)

; (1.2.4)

Большую информативность фазовых портретов даёт применение в качестве координат переменных и скорости её изменения ,причём переменная у откладывается по оси ординат.

Система уравнений (1.2.4) при этом преобразуется к виду:

Рис. 2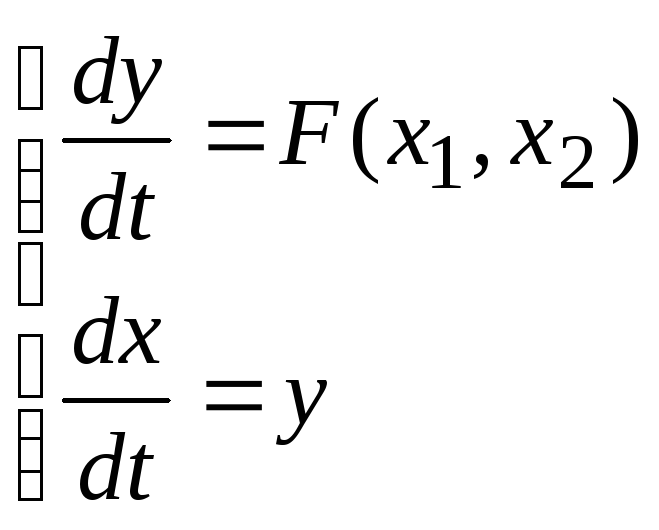

(1.2.5)

Фазовая плоскость с этой системой координат обладает следующими свойствами:

а) в верхней полуплоскости (рис.1.2.2) направление движения по траекториям слева направо, т.е. в сторону увеличения x, так как там скорость y>0, а в нижней полуплоскости, наоборот, – справа налево

б) ось x пересекается фазовыми траекториями под прямым углом, т.к. в точках пересечения скорость y=0, т.е. имеет место максимум или минимум величины x.

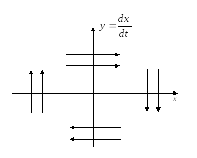
Рис.1.2.2

1 .3. Типы особых точек и фазовые траектории линейных систем

Рассмотрим линейную систему, движение в которой описывается уравнением:

Решим уравнение (1.8) относительно старшей производной

Введем новую переменную

,=

Разделим (1.10) на (1.11) и получимдифференциальное уравнение (ДУ) фазовых траекторий

Решение y = f(x) этого ДУ определяет собой некоторое семейство интегральных кривых на фазовой плоскости (x,y), каждая из которых соответствует одному определенному значению произвольной постоянной. Совокупность интегральных кривых (фазовый портрет) представляет собой все возможные фазовые траектории, а значит все возможные виды переходных процессов в замкнутой САУ при различных начальных условиях. .

В точках, соответствующих установившемуся состоянию ( x=0, y=0), получаем согласно уравнению (1.12) выражение

то есть неопределенное направление касательных к интегральным кривым. Эти точки называют особыми и они классифицируются, т.е. им присвоены названия.

Уравнению (1.8) соответствуют корни характеристического уравнения

(1.14)

В зависимости от знаков и величины коэффициентов a₁ и а₂ возможны шесть случаев корней характеристического уравнения и соответствующих им фазовых траекторий.

Рассмотрим эти случаи подробнее:

1. a₁=0, a₂>0 – корни чисто мнимые.

Линейная система на границе устойчивости (в системе возникают незатухающие колебания).

2. a₁>0, a₂>0, дискриминант D<0 – корни комплексные с отрицательными вещественными частями. Линейная система устойчива, процессы колебательные, затухающие.

3. a₁<0, a₂>0, дискриминант D<0 – корни комплексные с положительными вещественными частями.

Линейная система неустойчива, процессы колебательные расходящиеся.

4. a₁>0, a₂>0, дискриминант D>0 – корни вещественные, отрицательные. Линейная система устойчива, процессы апериодические.

5. a₁<0, a₂>0, дискриминант D>0 – корни вещественные, положительные. Линейная система неустойчива, процессы апериодические.

6. a₁>0, a₂<0, D>0 – корни вещественные, разных знаков. Линейная система неустойчива, процессы апериодические.

Рассмотрим фазовые траектории для каждого случая в отдельности.

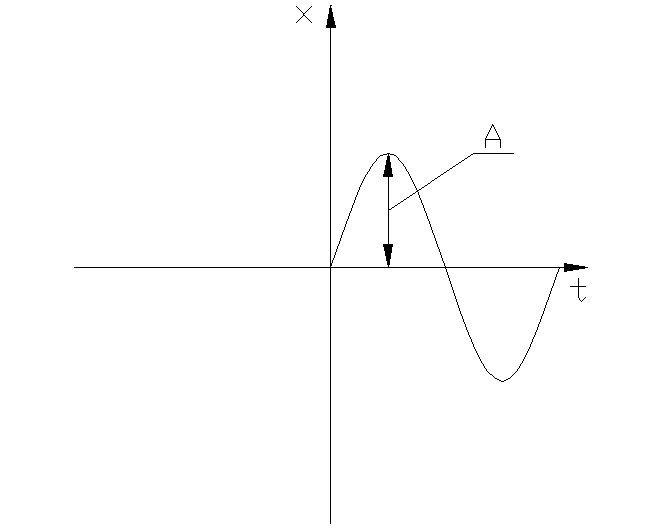1. Если рассматривать движение от оси абсцисс, то можно записать ,, а величиныА и определяются начальными условиями.

A

Рис. 1.3.1а

Рис. 1.3.1.б

О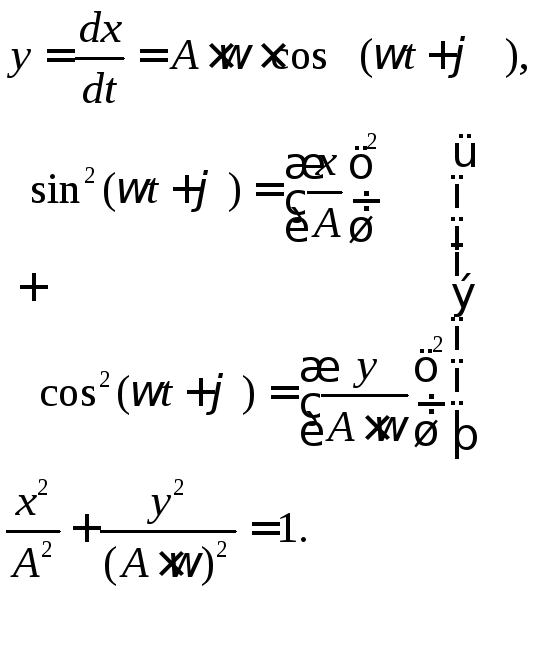

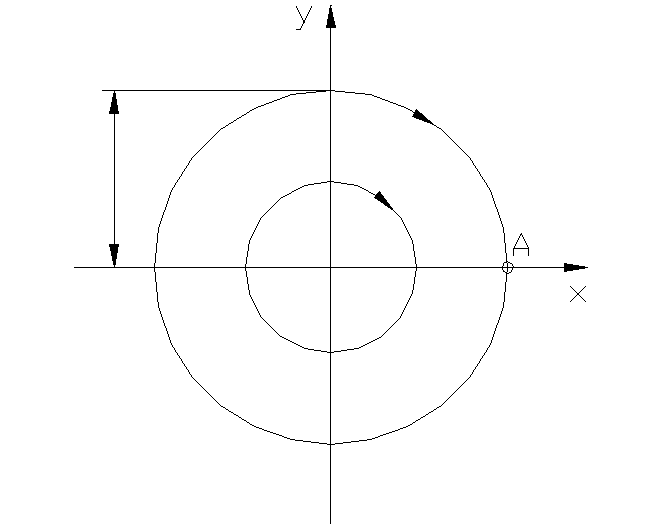
Незатухающим колебаниям в системе (рис.1.3.1а) соответствует движение изображающей точки М (рис.1.3.1б) по замкнутым траекториям эллиптического вида.

Точка О (x=0; y=0) – особая точка, центр.

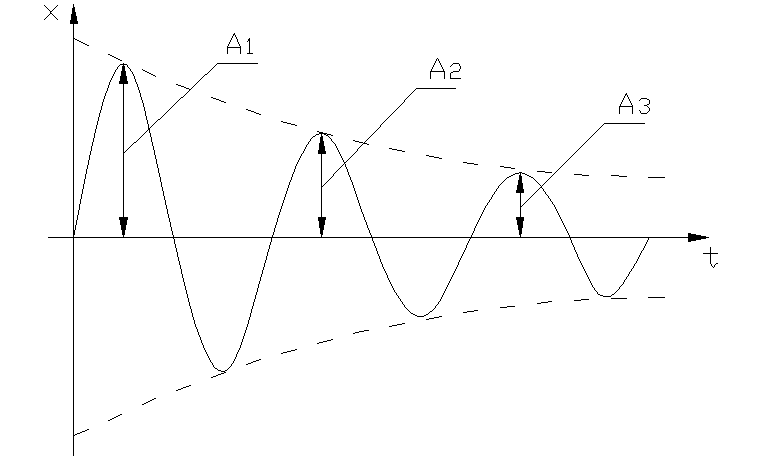
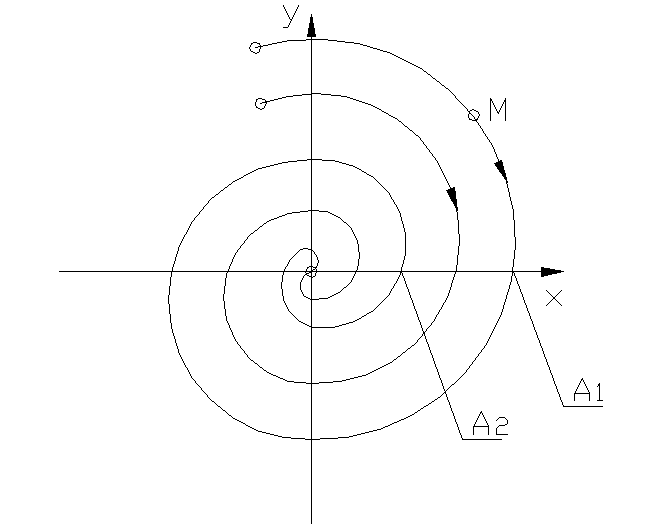
2. Корни комплексные с отрицательными вещественными частями

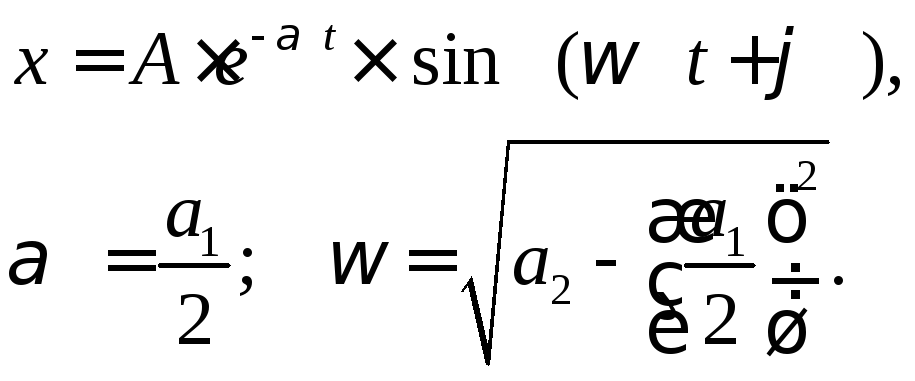
О

Рис. 1.3.2 а

Рис. 1.3.2 б

А₁> А₂>…> А_n

Затухающим колебаниям (рис.1.3.2а) в системе на фазовой плоскости (рис.1.3.2.б) соответствуют спиралевидные траектории, по которым изображающая точка стремится к началу координат. Точка О – особая точка – устойчивый фокус.

3. Корни комплексные с положительными вещественными частями.

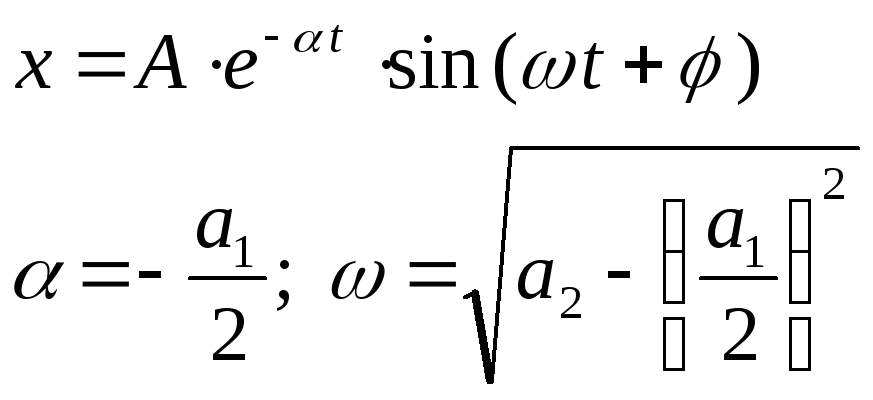
О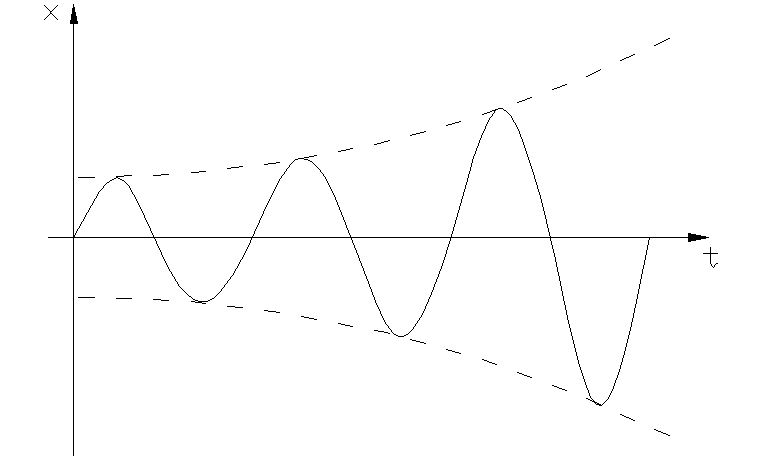

Рис. 1.3.3 а

Рис. 1.3.3 б

Расходящимся колебаниям в системе на фазовой плоскости соответствуют спиралевидные траектории, по которым изображающая точка удаляется от начала координат. Особая точка О – неустойчивый фокус.

4. Корни вещественные, отрицательные.

Переходные процессы апериодические двух типов: монотонные (1) и с перерегулированием (2).

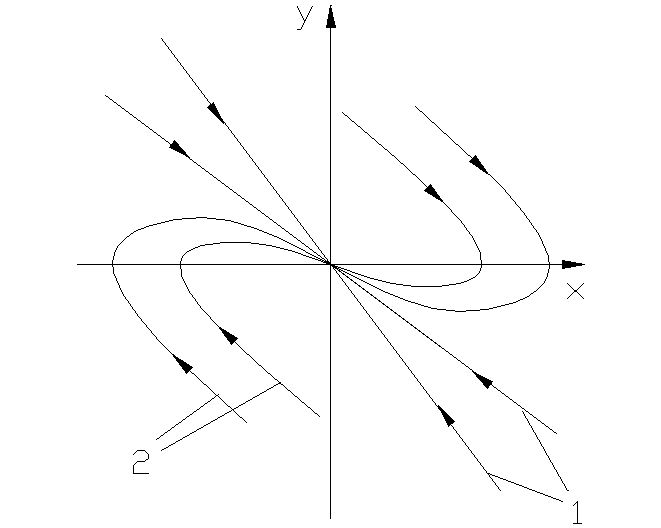
y=₂x

y=₁x

Рис. 1.3.4 б

Рис. 1.3.4 а

О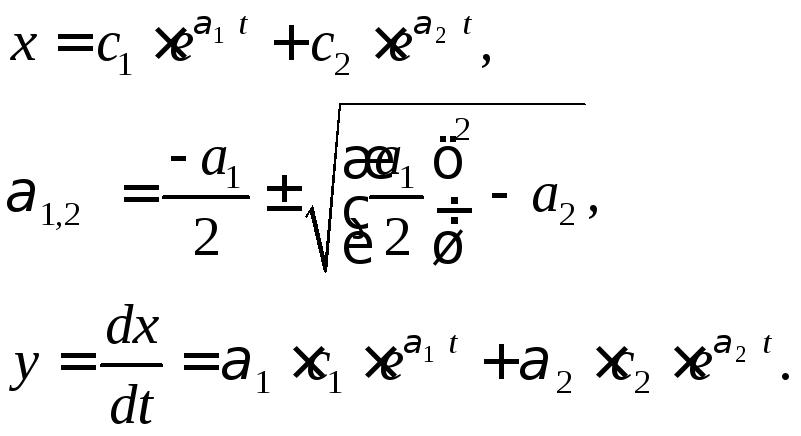

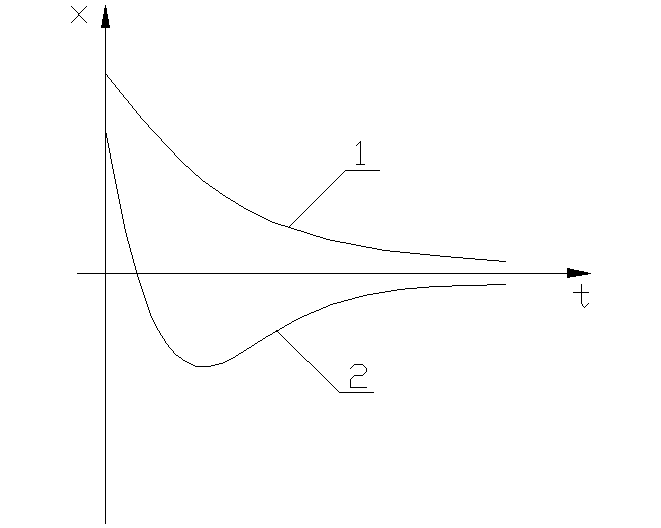
Монотонные процессы получаются при выполнении условий:

Соответствующие им фазовые траектории имеют вид прямых линий (рис.1.3.4б).

Особая точка О – устойчивый узел.

Фазовые траектории, имеющие точку равновесия в виде устойчивого узла, соответствуют апериодическому затухающему переходному процессу.

5. Корни вещественные, положительные.

y=₂x

y=₁x

Рис. 1.3.5 а

Рис. 1.3.5 б

О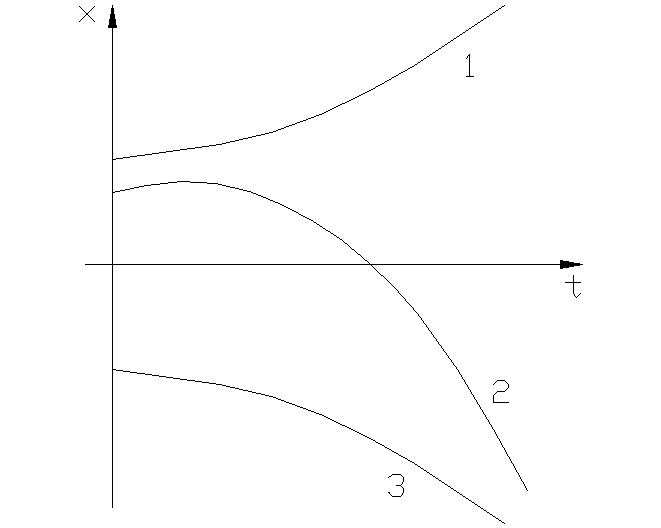

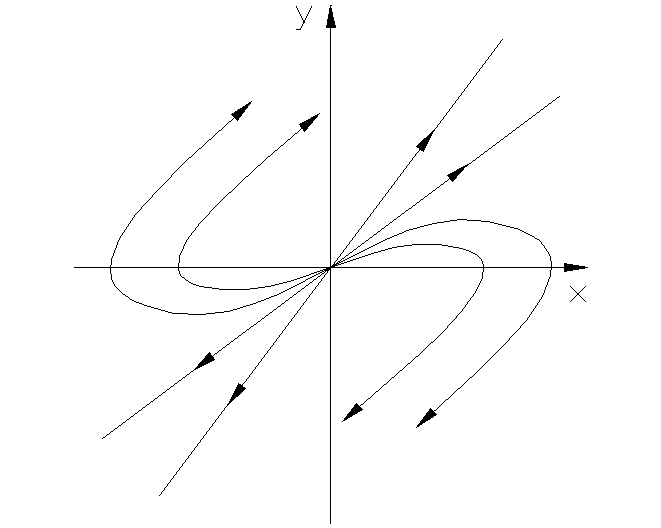
Выражения такие же, как в предыдущем случае, только α меняет знак

Движение изображающей точки направлено от точки равновесия системы к бесконечной удаленной точке фазовой плоскости. В этом случае положение равновесия системы неустойчивое.

Особая точка О – неустойчивый узел.

6

M

О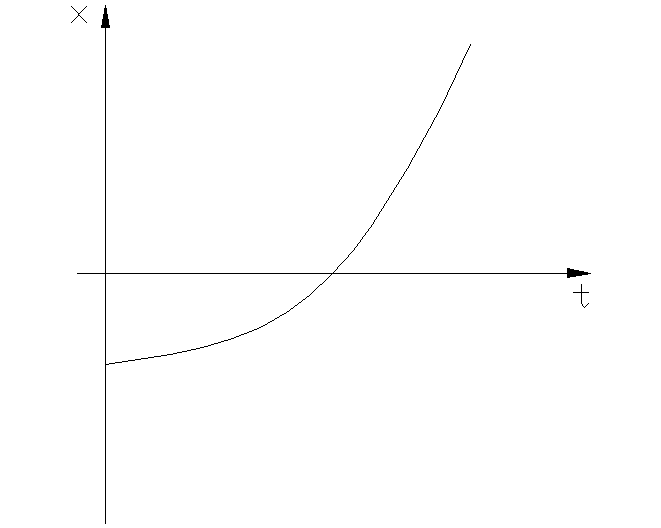

. Корни вещественные разных знаков.

П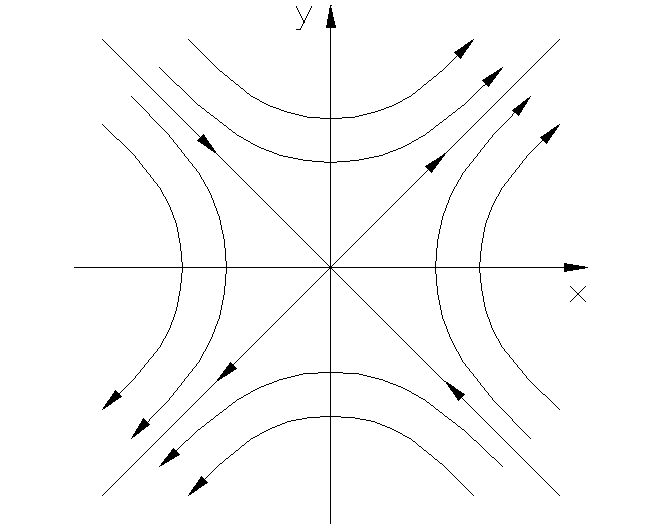роцессы апериодические неустойчивые (рис.1.3.6а).

Рис. 1.3.6 б

Рис. 1.3.6 а

Где С- постоянная интегрирования.

Фазовые траектории имеют вид гипербол. О

Рис. 10

собая точка О называется «седло».

Седло всегда неустойчиво.