4.7.2 Определение периодических режимов при несимметричных колебаниях

Рассмотрим нелинейную систему

Н.Э.

Л.Ч.

g x y z

-

Рис. 4.7.6

Связь между координатами на входе и выходе линейной части

(4.7.12)

(4.7.13)

Учитывая выражение (4.7.3) гармонической линеаризации нелинейного элемента и исключая промежуточные переменные, получим гармонически линеаризованное уравнение системы при несимметричных режимах

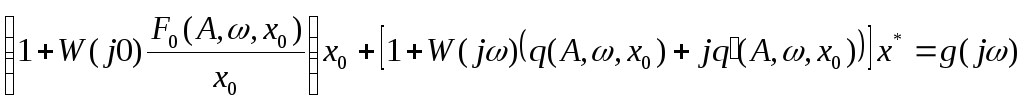; (4.7.14)

–коэффициент передачи линейной части,

–статический коэффициент передачи нелинейного элемента,

Предположим, что на заданном интервале времени А, ω и x₀ остаются постоянными, при этом уравнение (4.7.14) разбивается на два:

уравнение для постоянной составляющей

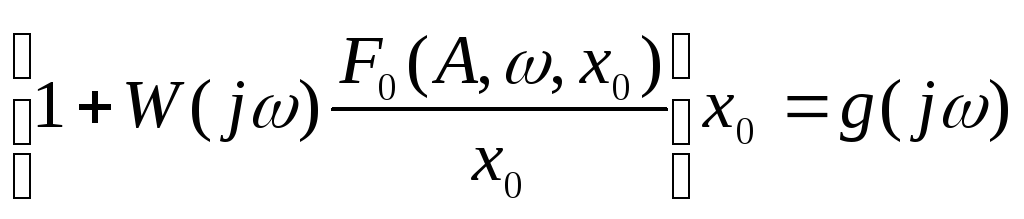, (4.7.15)

уравнение для периодических составляющих

. (4.7.16)

Система уравнений (4.7.15, 4.7.16) может быть решена алгебраическим путем. Для этого во втором уравнении системы выделяется действительная и мнимая части, их почленно приравнивают к нулю.

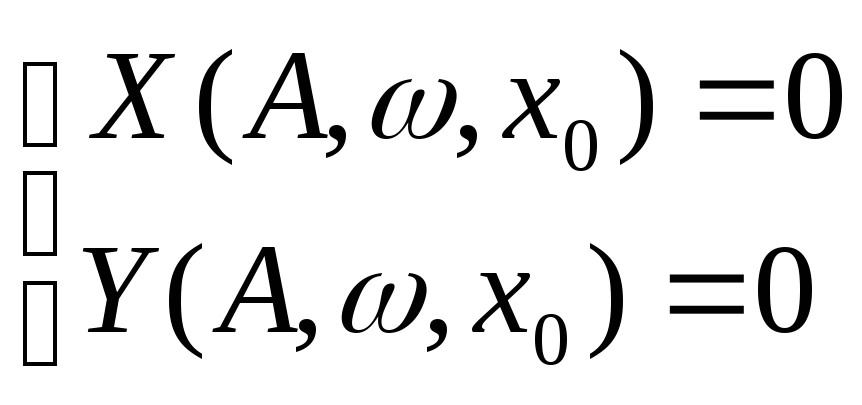
(4.7.17)

В итоге получаем систему из трёх уравнений (4.7.16), (4.7.17) и три неизвестных: А, ω, x₀. Эта система совместная ,следовательно, могут быть найдены переменные А, ω, x₀ .

А

(4.7.18)

(4.7.19)

втоколебания могут быть найдены и частотными методом. Если известноx₀, то характеристическое уравнение замкнутой системы представляется в виде

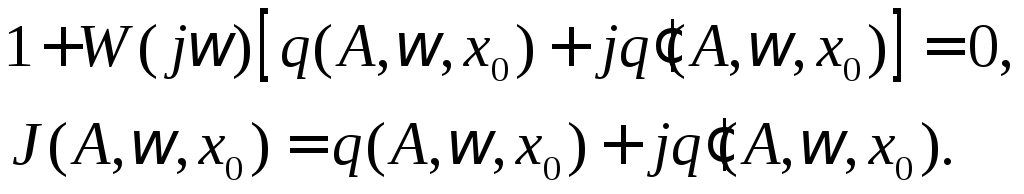
Затем графически решается уравнение

.

Строится годограф АФХ линейной части и обратный годограф АФХ Н.Э. Откуда находятся A и  автоколебаний.

В качестве примера рассмотрим методику исследования несимметричных периодических режимов при постоянном входном воздействии.

Предположим, что g(jω)=g₀ – постоянная величина, и рассмотрим методику определения несимметричных автоколебательных режимов частотным методом.

Рассмотрим более простой случай, когда нелинейность имеет вид у=F(x), при этом коэффициенты гармонической линеаризации зависят от амплитуды А, смещения x₀ на выходе Н.Э. и имеют вид q(А,х₀), q'(А,х₀) и F₀(А, x₀).

1. Записываются уравнения для постоянных составляющих

; - статический коэффициент передачи линейной части, при =0.

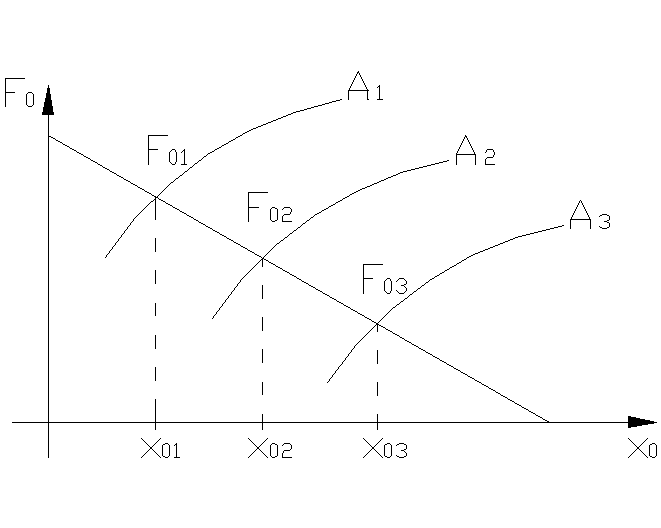
2. С

   А₁>A₂>A₃

   троится прямая линия

3. П

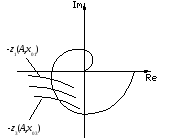
   Рис. 4.7.7

   о известным выражениям (4.7.6) гармонической линеаризациидля ряда фиксированных значений амплитуды и переменной 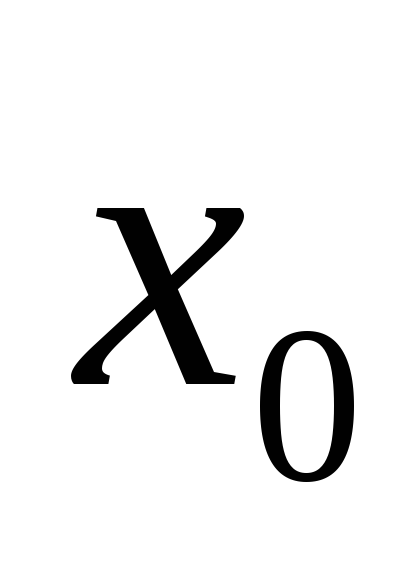строится (рис.4.7.7) семей-ство характеристик.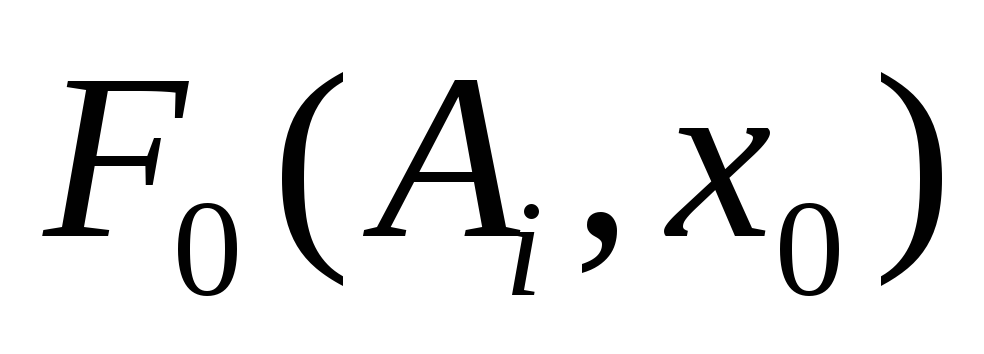

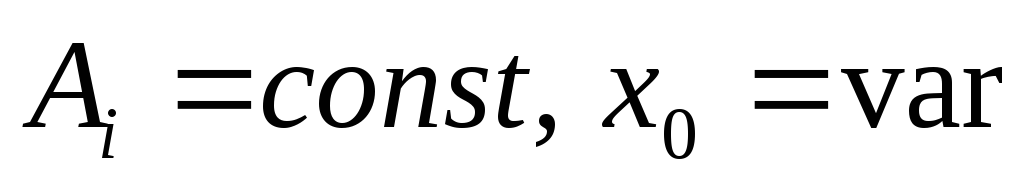4. Строим годограф АФХ W(jω) линейной части.

З

X₀₁

X₀₂

X₀₃

атем для ряда дискретных значенийх₀ и переменной А строим семейство обратных АФХ Н.Э. _{и определяем устойчивость автоколебаний.}

В

W(jω)

соответствии с критерием –автоколебания устойчивы.

Х₀₁<X₀₂<X₀₃

Рис. 4.7.8

5

Рис. 66

. По точкам пересечения кривых с прямой строим (рис.4.7.9) график A(х₀).

6. По точкам пересечения годографа АФХ линейной части с обратной АФХ нелинейного элемента строим (рис.4.7.9) кривую х₀(А).

X₀₁

X₀₃

X₀₂

A₃A₂

A₁

Рис. 4.7.9

7

Рис. 4.7.9

. Графическое решение уравненийА(х₀) и х₀(А) даёт искомые параметры устойчивых автоколебаний: Х_0у и А_0у.

Г





лава 5. Преобразование структурных схем нелинейных САУ

Для исследования устойчивости автоколебательных режимов многоконтурные нелинейные системы с помощью структурных преобразований необходимо приводить к одноконтурным, одного из следующих видов:

. (5.1 а)

Рис. 5.1 а

Рис. 5.1 б

Рис. 5.1 в

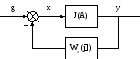
.(5.1 б)

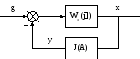
.(5.1 в)

Все структуры позволяют найти характеристическое уравнение :

, (5.1.д)

поэтому определение параметров и устойчивости автоколебаний можно проводить по любой из выше представленных структур.

Из этого рассмотрения видно, что первым этапом анализа устойчивости нелинейных САУ является выполнение структурных преобразований, а вторым этапом составление уравнения (5.1.д).

Структурные преобразования нелинейных систем можно производить линейным и нелинейным способом. Преобразования в нелинейных системах отличаются от преобразований в линейных САУ, т.к. амплитуда сигнала на входе НЭ должна оставаться неизменной независимо от выполняемых преобразований, поэтому линейные звенья нельзя переносить через нелинейный элемент. Линейные преобразования выполняются по известным правилам и являются эквивалентными, т.е. передаточная функция замкнутой системы до преобразования равна передаточной функции замкнутой системы после преобразования. После нелинейных преобразований с исходным совпадает только характеристическое уравнение (5.1.д).

Рассмотрим несколько примеров с линейными и нелинейными преобразованиями структурных схем.

Пример 1. Нелинейность в прямом пути внутреннего контура .

Рис. 5.2

Запишем по формуле Мэзона ПФ замкнутой гармонически линеаризованной нелинейной САУ . (5.2)

Проведём линейные преобразования структурной схемы

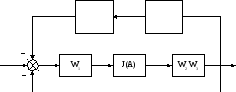
Рис. 5.3

Просуммируем обратные связи. Ввести переменные g, z

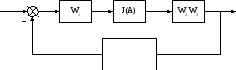
Рис. 5.4

В окончательном виде:

Ввести переменные g, z

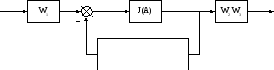
Рис. 5.5

Для проверки запишем ПФ замкнутой нелинейной САУ

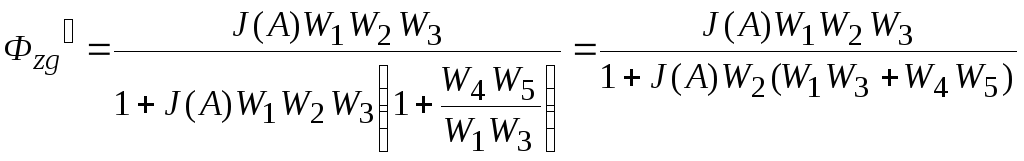(5.3)

Из совпадения выражений (5.3) и (5.2) делаем вывод, что преобразования выполнены верно.

Пример2. Преобразование структурной схемы нелинейным способом

Нелинейные преобразования основаны на отключении одной из линий связи и вынесении нелинейностей из внутреннего контура. Такие преобразования не являются эквивалентными. Они позволяют получить то же самое характеристическое уравнение, но не передаточную функцию замкнутой системы.

Разрываем схему и выносим нелинейность из внутреннего контура.

Рис. 5.6

Характеристический полином замкнутой системы

, (5.4)

совпадает по виду со знаменателем исходной передаточной функции (5.2), но числитель ПФ будет отличаться от числителя (5.2.). Следовательно, преобразованная структурная схема не позволяет построить эквивалентные переходные процессы.

Пример 2 . Нелинейность в цепи местной обратной связи

Рис. 5.7

Разомкнём линию связи за нелинейностью и извлечём НЭ из внутреннего контура

Рис. 5.8

Рис. 5.9

Место разрыва устранено соединением точек А и Б линией связи.

Найдём характеристическое уравнение структуры (рис. 5.9)

(5.5)

(5.6)

По исходной структурной схеме (рис.5.7) получим ПФ замкнутой системы

.(5.7)

Как видно, знаменатель выражения (5.7) является совпадает с характеристическим уравнением (5.6).

Если в структурных схемах встречаются две нелинейности, расположенные рядом (рис.5.10), то они объединяются в одну эквивалентную нелинейную характеристику (рис.5.11). Затем преобразование структурных схем проводят веше рассмотренными способами.

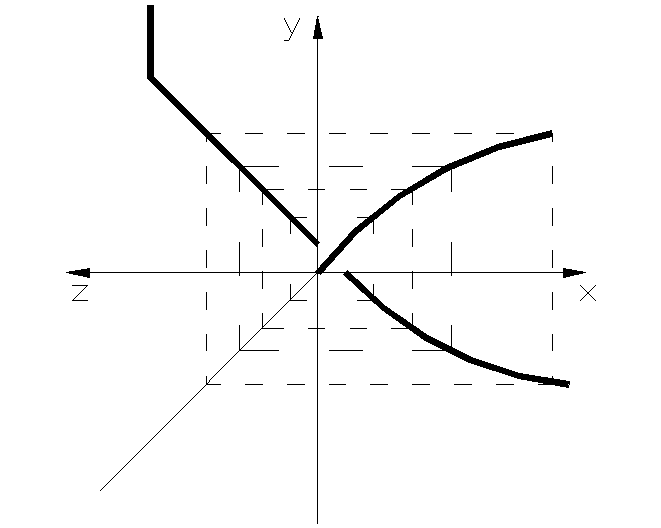
y

z

x

Н.Э.₁

Н.Э.₂

Рис. 5.10

Рис. 5.11

Г





лава 6. Нелинейные системы с коррекцией.