7.4. Частотный критерий абсолютной устойчивости

(критерий В.М. Попова)

Румынский учёный В.М.По'пов предложил частотный метод определения абсолютной устойчивости положения равновесия нелинейных систем. Рассматривается устойчивость собственного движения нелинейной системы, состоящей из двух звеньев.

g x y z

Н.Э.

W_л(s)

-

Рис. 7.4.1

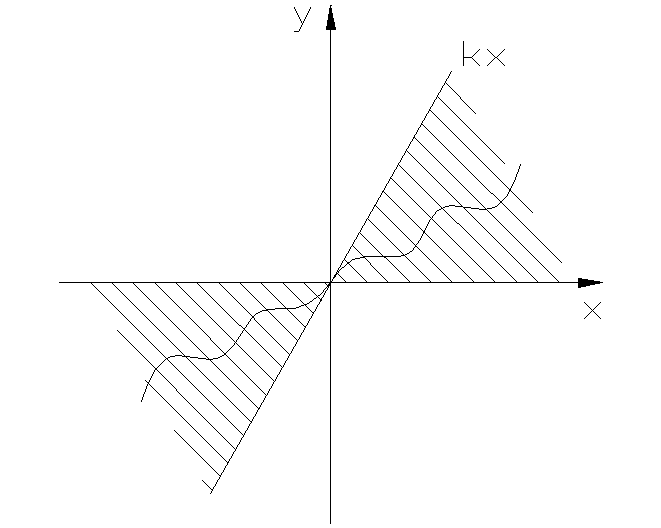
На нелинейность накладываются следующие ограничения:

- однозначная нелинейная функция любой формы, принадлежащая сектору (0,k) и проходящая через начало координат.

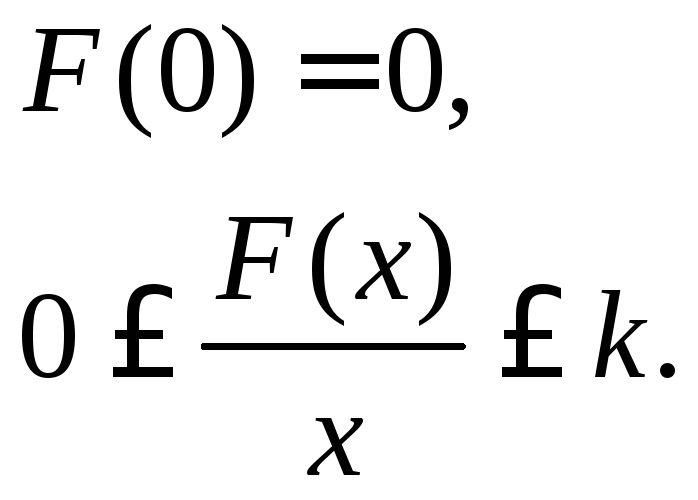
Рис. 7.4.2

Остальные полюса должны лежать в левой полуплоскости.

Теорема В.М.Попова: для установления абсолютной устойчивости положения равновесия нелинейной системы достаточно подобрать такое действительное число h>0, чтобы при всех выполнялось условие :

(7.4.1) где k – коэффициент, ограничивающий сектор, внутри которого должна лежать нелинейность .

При наличии одного нулевого полюса требуется выполнение условия: .

При наличии двух нулевых полюсов требуется выполнение условия: .

Графическая интерпретация уравнения 7.4.1.

Для удобства графической интерпретации введем модифицированные частотные характеристики линейной части.

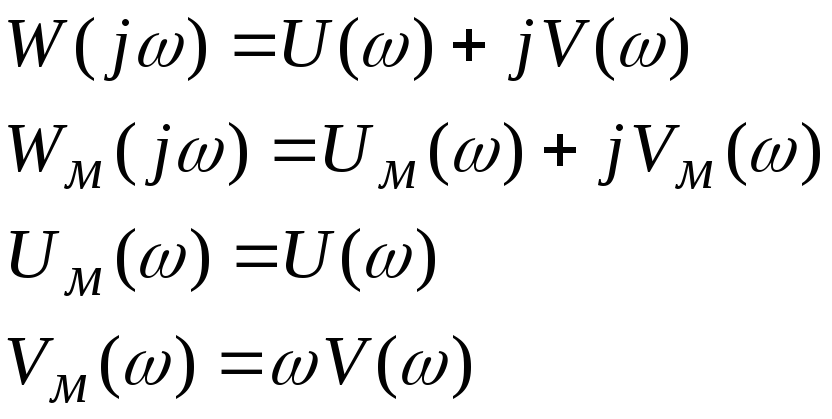(7.4.2)

Модифицированная АФХ W_M(jω) имеет особенности, отличающие её от W(jω). Если разность степеней , то годограф заканчивается на мнимой оси (рис.7.4.3). Если , то W_M(jω) и W(jω) совпадают при ω=0, ω=1 и ω=∞.

W_м(jω)

Рис.7.4.3

jV_м

Найдем вещественную часть выражения 7.4.1.

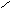
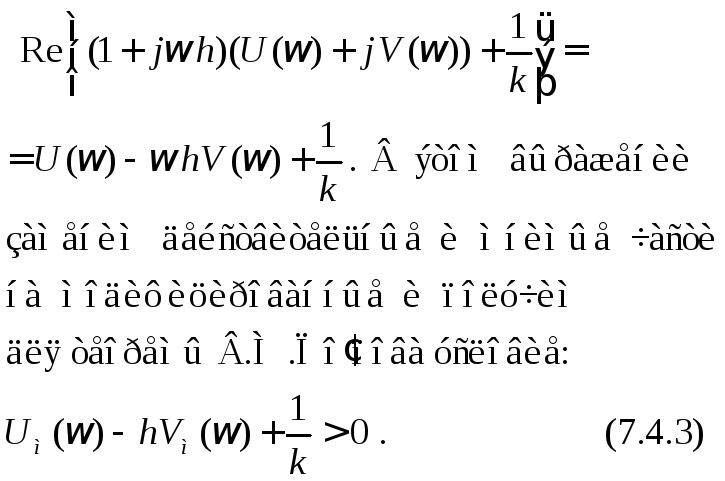
Рис. 7.4.4

Рис. 7.4.3

Если в (7.4.3) знак неравенства заменить равенством

, (7.4.4)

то получим уравнение (7.4.4) прямой линии на комплексной плоскости , проходящей через точку.

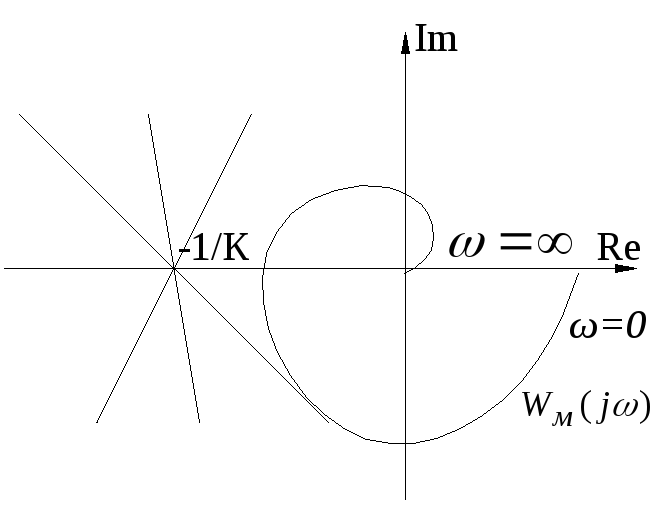
Отсюда вытекает графическая интерпретация теоремы В.М.Попова: для установления абсолютной устойчивости нелинейной системы достаточно на плоскости подобрать такую прямую, проходящую через точку, чтобы годограф модифицированной АФХлежал справа от этой прямой (рис.7.4.4).

На рис. 7.4.5 показаны случаи невыполнения теоремы.

Рис. 7.4.5 а

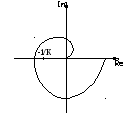
Рис. 7.4.5 б

П

Рис. 7.4.5

ример.

Нелинейная система второго порядка имеет передаточную функцию линейной части вида:

(7.4.4)

ω₀ – величина, обратная постоянной времени.

Необходимо определить, при каких значениях k система будет абсолютно устойчива, если характеристика нелинейного элемента лежит в секторе (0,k).

Модифицированная АФХ имеет вид:

jV_м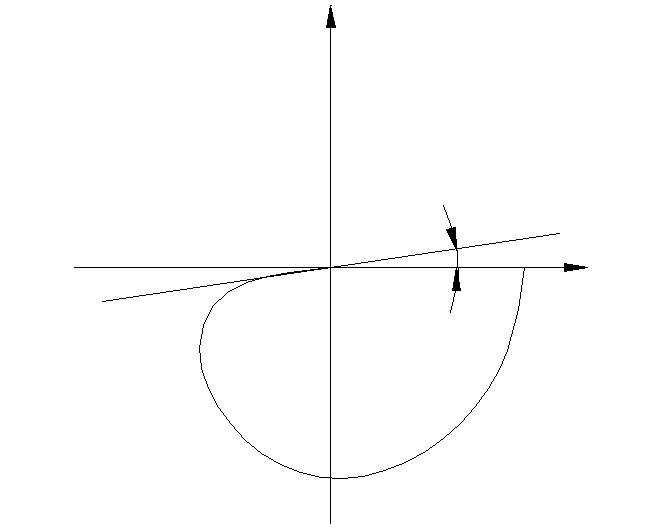



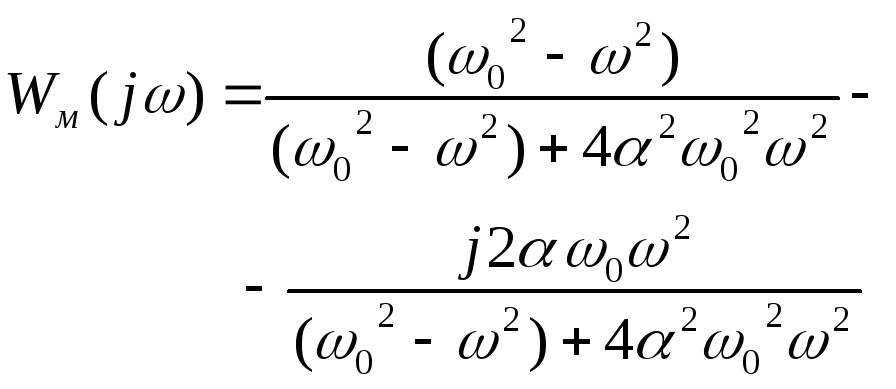
Мнимая часть годографа модифицированной АФХ при всех значениях  отрицательна, т.е. годограф лежит в нижней плоскости и при совпадает с

Из анализа графика АФХ можно сделать вывод, что система абсолютно устойчива при любых значениях k, вплоть до k = ∞, т.к. в начале координат (ω=∞) кривая лежит правее касательной с углом β к вещественной оси. Поэтому всегда можно провести прямую Попова через точку -1/К под некоторым углом β. Таким образом, система абсолютно устойчива при всех К , если однозначная нелинейная характеристика принадлежит сектору (0, ∞). Т.е. нелинейная характеристика должна лежать в первом и третьем квадрантах и может иметь при этом любую форму.

Обобщение критерия Попова на случай неустойчивости линейной части.

Если линейная часть системы неустойчива, то нелинейная характеристика не может принадлежать сектору (0,k), т.к. при k=0, что соответствует разомкнутой системе, получается заведомо неустойчивая система, т.к. неустойчива линейная часть. Неустойчивость сохраняется и в области малых значений k. Для применения критерия Попова к САУ с неустойчивой линейной частью, структурную схему системы преобразуют путем охвата линейной части отрицательной жесткой обратной связью с коэффициентом r, а нелинейного элемента параллельной отрицательной связью с коэффициентом r.

f(x)

W_л(s)

-

Рис. 7.4.6

Рис. 7.4.7

f(x)

W_л(s)

-

-

-

r

r

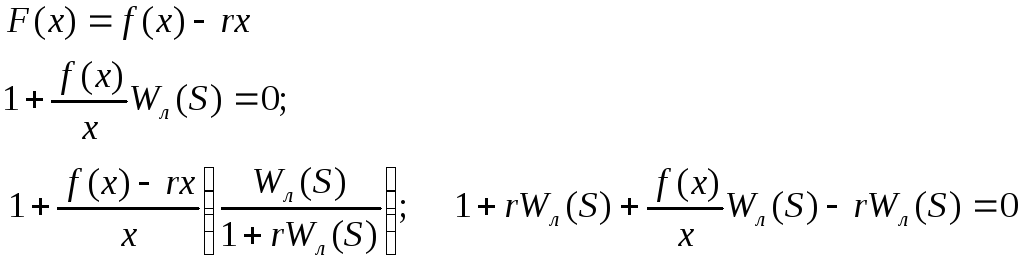(7.4.5)

Коэффициент r выбирают таким образом, чтобы контур с неустойчивой передаточной функцией W(S) стал устойчив, т.е. чтобы передаточная функция преобразованной линейной части была устойчива.

Устойчивость определяется по критерию Найквиста.

Условие устойчивости В.М. Попова в этом случае:

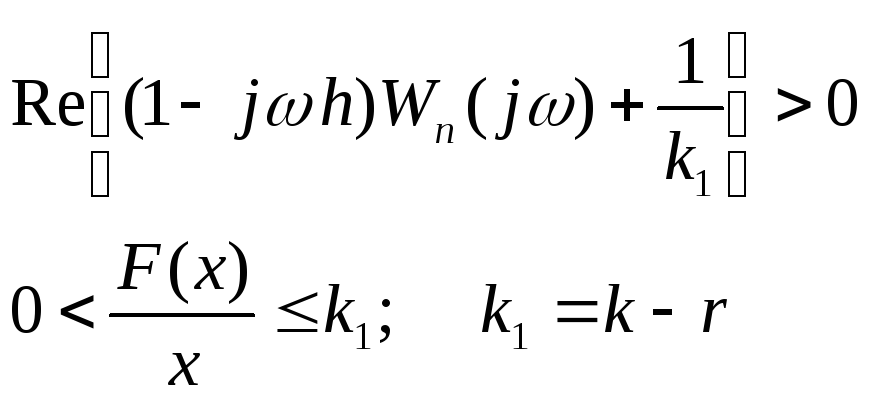(7.4.6)