Глава 2. Фазовая плоскость систем, описываемых уравнениями с неаналитической правой частью

В дифференциальных уравнениях с неаналитической правой частью, последняя не раскладывается в ряды по степеням аргументов (х,у).

2 .1. Исследование системы со скользящим режимом

Рассмотрим систему, которая содержит объект с самовыравниванием, безынерционный чувствительный элемент, усилитель мощности (золотник) и серводвигатель постоянной скорости.





-





Рис. 2.1.1

 - регулируемая переменная

 - выходная величина чувствительного элемента

 - выходная величина У.М.

 - регулирующее воздействие

В общем случае объект управления с самовыравниванием описывается уравнением:

Где:

- постоянная времени,

- коэффициент самовыравнивания,

- если >0 – объект статически устойчив, и задачей регулятора является обеспечение требуемого качества управления;

-если <0 – объект статически неустойчив,

-если =0 – объект нейтрален.

В двух последних случаях задачами регулятора являются: во-первых, обеспечение устойчивости, во-вторых, обеспечение требуемого качества управления.

Рассмотрим случай нейтрального объекта т.е. =0, тогда:

.(2.1.1)

Уравнение серводвигателя постоянной скорости 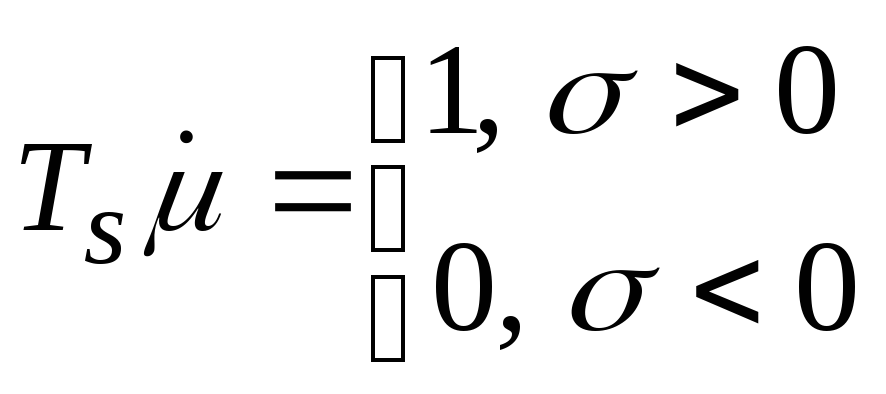(2.1.2)

Уравнение золотника с жесткой обратной связью (2.1.3)

γ – коэффициент жесткой обратной связи

Уравнение безынерционного чувствительного элемента (ЧЭ)

(2.1.4)

 - коэффициент, характеризующий чувствительность ЧЭ

Исключим промежуточные переменные μ, σ, η

Для этого, продифференцировав уравнение (2.1.1), решим (2.1.1, 2.1.2, 2.1.3, 2.1.4) относительно старшей производной выходной переменной и получим:

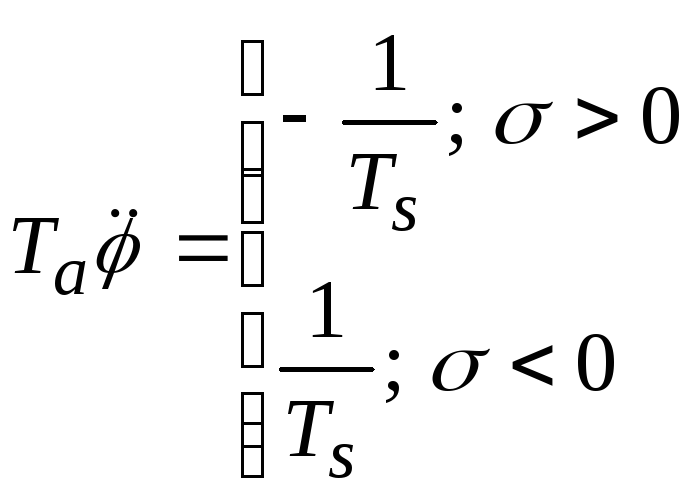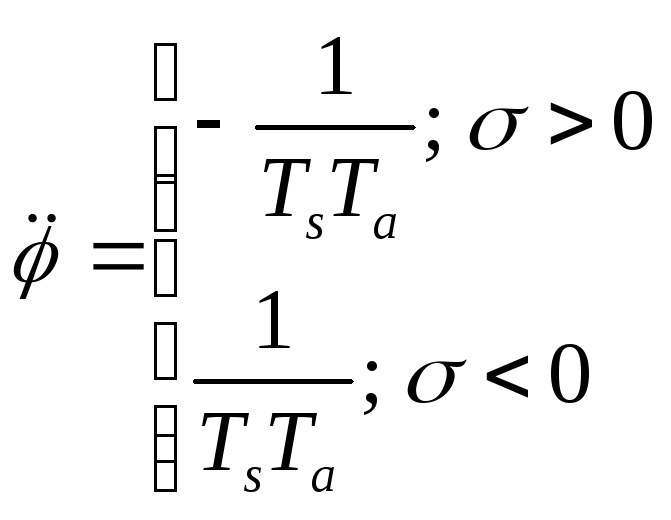; ; (2.1.5)

Исключим переменную σ:

Таким образом,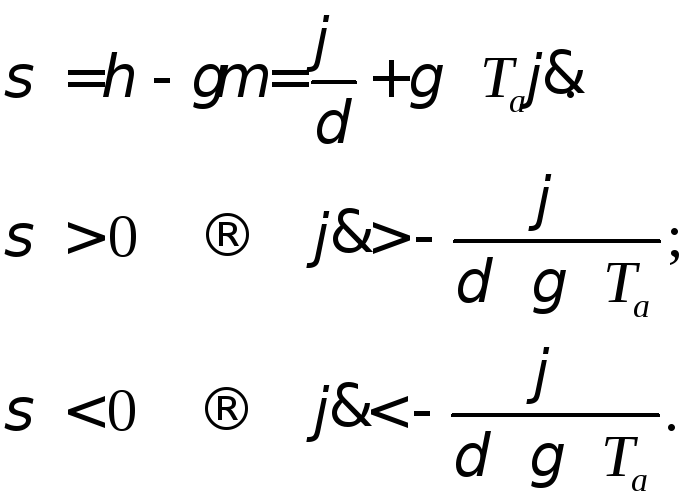

С учетом изложенного

(2.1.6)

З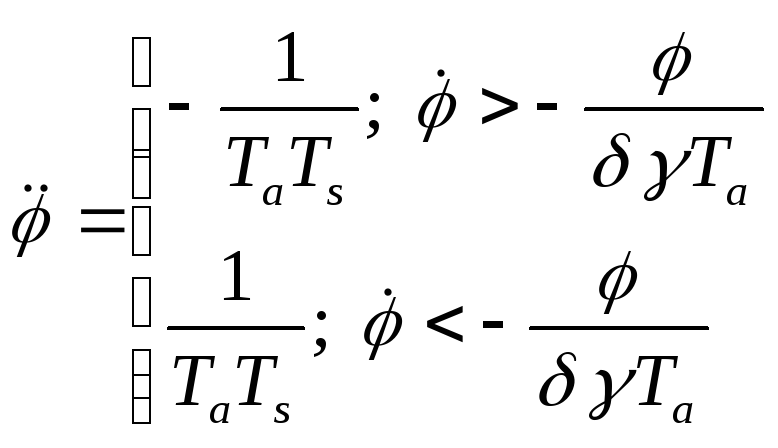аменим переменные

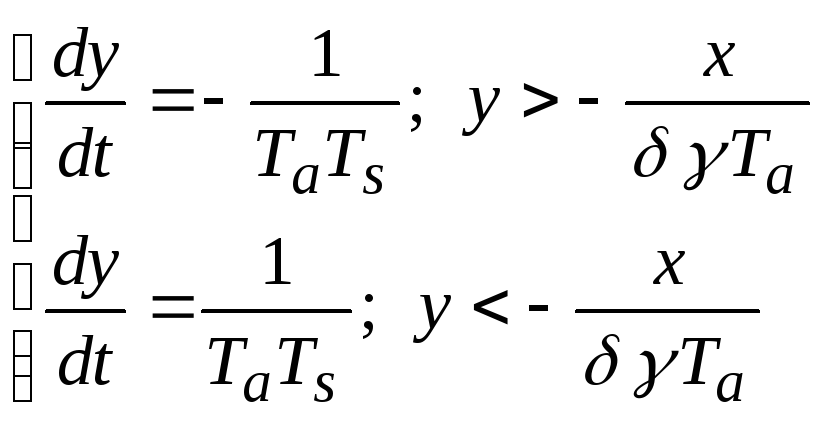(2.1.7)

Учитывая что , (2.1.8)

исключим в (2.17) переменную время t . Для этого разделим выражения (2.1.7) на (2.1.8):

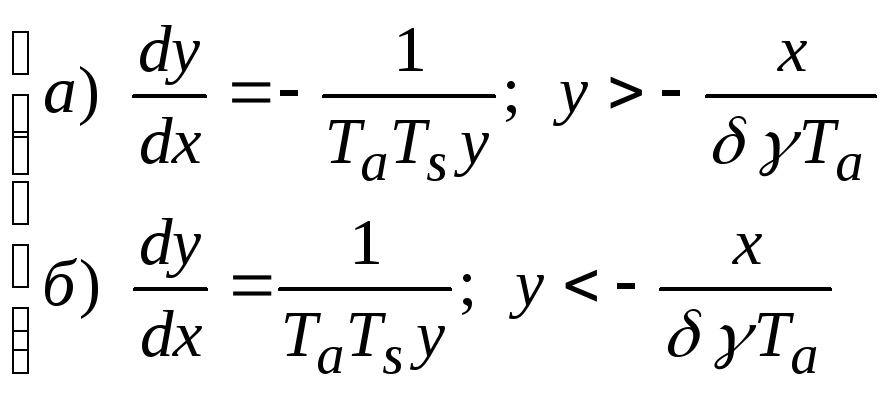(2.1.9)

Проинтегрируем выражения (2.1.9), получим уравнения интегральных кривых, определяющих траектории на фазовом портрете

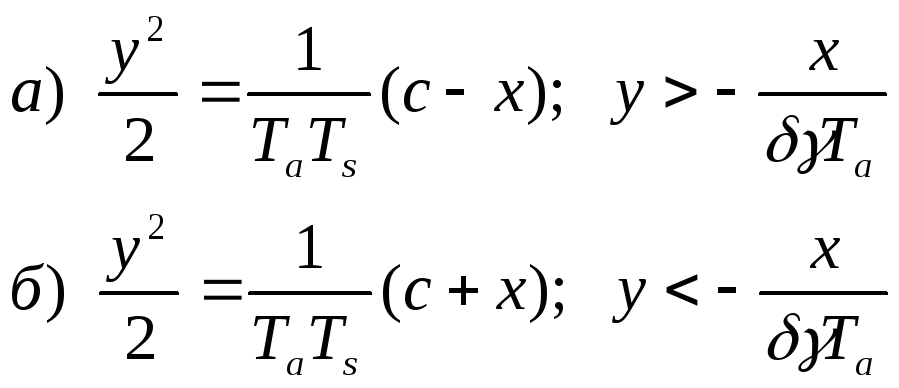(2.1.10)

Уравнение линии переключения получим, заменяя в условии знак неравенства знаком равенства:

Рис. 2.1.2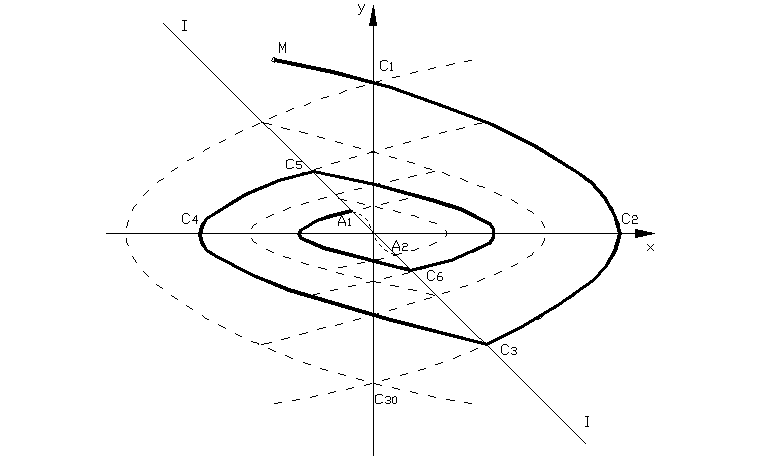

(2.1.11)

Рассмотрим фазовый портрет системы. Область справа от линии переключения I-I заполнена траекториями (параболами) семейства 2.1.10а, а слева – семейства 2.1.10б.

При отсутствии внутренней жесткой обратной связи линия переключения совпала бы с осью ординат и точка М, двигаясь по траектории С₁С₂С₃₀ семейства 2.1.10а, переходила бы в точке С₃₀, на симметричную траекторию С₃₀С₁ семейства 2.1.10б. Этой замкнутой траектории соответствовали бы автоколебания в системе. Из-за наличия внутренней обратной связи (), переход с параболы семейства 2.1.10а на параболу семейства 2.1.10б происходит на линии переключения в точке С₃ и, двигаясь по параболе С₃С₄С₅, а в точке С₅ происходит переход на траекторию семейства 2.1.10а и т.д. С каждым полуколебанием изображающая точка приближается к началу координат – к равновесному состоянию. Это соответствует о затухающим колебаниям в системе. Однако, при попадании точки М на отрезок А₁А₂, характер движения становится существенно иным.

Точки А₁ и А₂ являются точками пересечения линии переключения I-I с параболами семейства 2.1.10а и 2.1.10б, проходящими через начало координат.

Е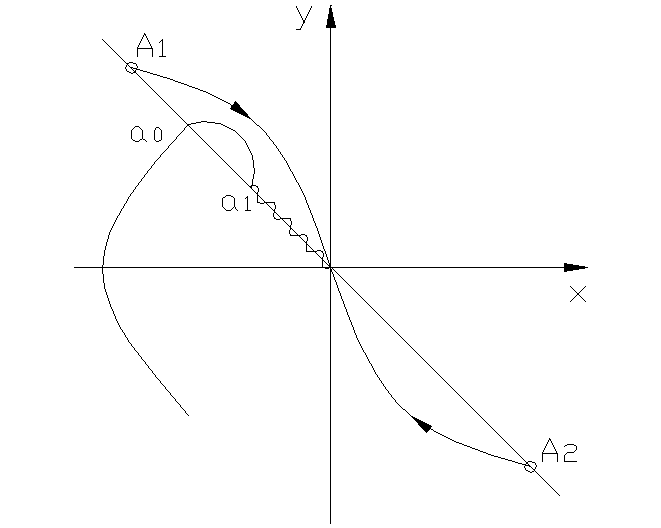сли изображающая точка М попадает на особый отрезок А₁А₂, например, в точку а₀, то в дальнейшем изображающая точка скользит вдоль линии переключения из-за непрерывного реверсирования серводвигателя.

Начиная с точки А₁, начинается скользящий режим. Скольжение происходит по линии переключения до начала координат.

Рис. 2.1.3

Найдем закон движения в скользящем процессе. На линии переключения уравнение движения будет иметь вид: . (2.1.12)

Рис. 20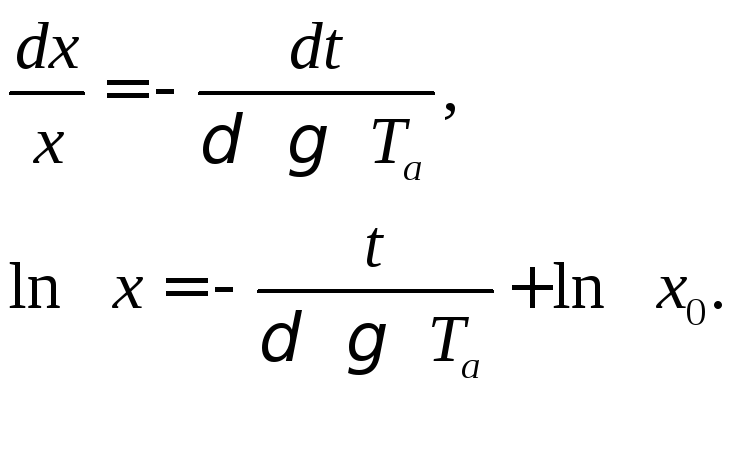

, . (2.1.13)

– является решением уравнения (2.1.12).

Значения x₀ и t отсчитываются с момента попадания точки М на линию скользящего режима.

Особенность скользящего режима заключается в том, что в данном режиме нелинейная колебательная система 2-го порядка вырождается в линейную систему первого порядка. При этом закон движения в скользящем режиме не зависит от параметров прямой цепи системы и определяется только коэффициентом обратной связи.