7.3. Выбор функций Ляпунова

В общем случае для всякой системы дифференциальных уравнений относительно нетрудно подобрать определенно положительную функцию V(x₁,_,...,x_n), которая может служить функцией Ляпунова. Основной проблемой данного метода является то, что не всякая такая функция имеет знакоопределенную или знакопостоянную производную W.

А.М.Ляпунов рекомендовал сначала выбирать отрицательно определенную функцию , а затем определять соответствующую положительную функцию .

Для линейных системa функцию ищут в виде квадратичной формы :

(7.3.1)

Для определения коэффициентов B_ij задаются функцией в виде отрицательной квадратичной формы:

(7.3.2)

Предположим, что уравнения, описывающее динамику системы, имеют вид:

(7.3.3)

Тогда из выражения (7.31) с учетом (7.3.3) получим выражение для производной:

(7.3.4)

Приравняв выражения (7.3.4) и (7.3.2), получим:

Затем, сгруппировав и приведя подобные члены, можно приравнять коэффициенты в левой и правой части. В итоге получим уравнения для определения коэффициентов B_ij:

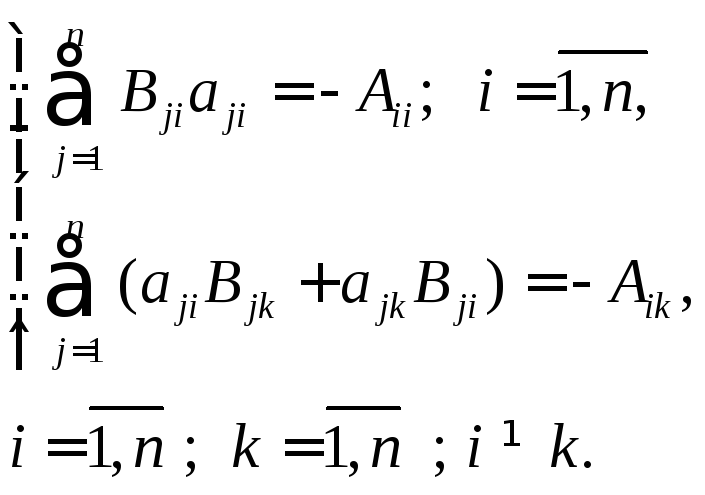(7.3.5)

Полагая величины заданными, можно решить систему (7.3.5) относительно коэффициентов и, получив в результате функцию , производная которой имеет заданный вид.

Коэффициенты при этом назначаются так, чтобы функция была заведомо знакоопределенной. Это можно сделать разными способами, например, принять

Тогда производная имеет определённо отрицательный вид.

В этом случае коэффициенты определяются из системы уравнений:

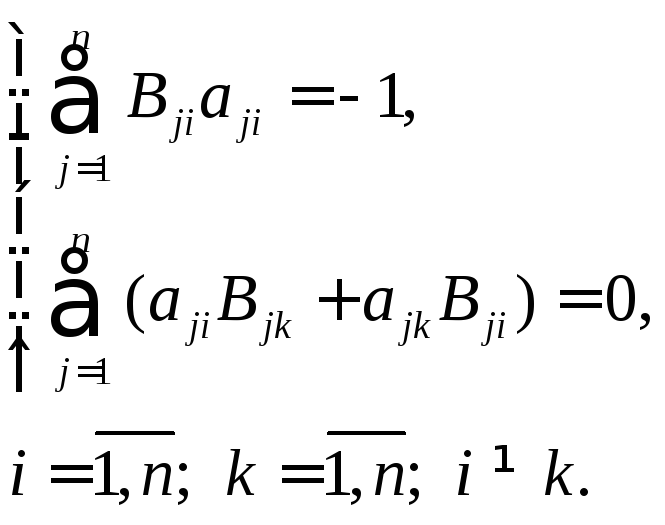(7.3.6)

Пример:

выбор функции Ляпунова для линейной системы второго порядка (n=2).

(7.3.7)

(7.3.8)

Примем

.

Предположим, что уравнения возмущённого движения системы имеют вид:

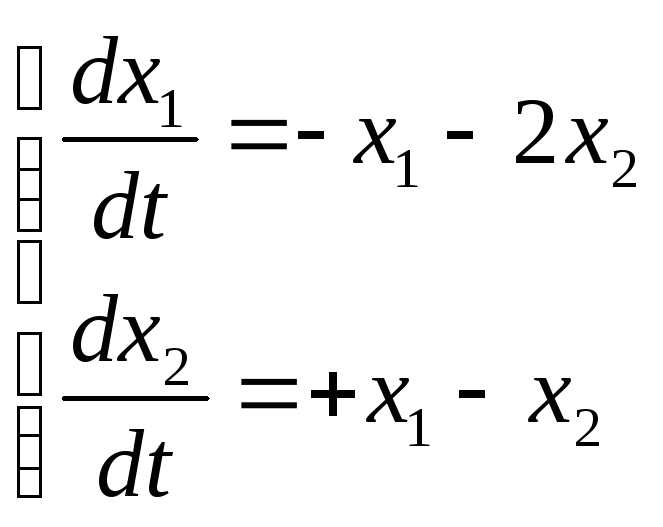(7.3.9)

Откуда найдём значения коэффициентов

(7.3.10)

Используя формулы соответствия:

(7.3.11)

получим

(7.3.12)

Учитывая значения коэффициентов (7.3.10):

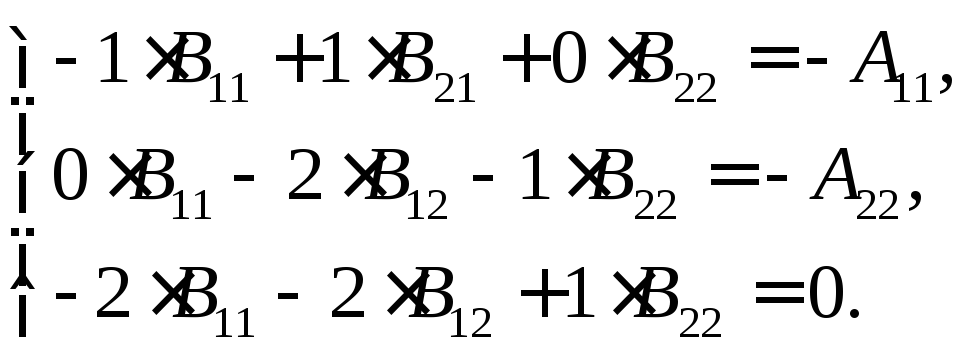(7.3.13)

Примем

(7.3.15)

и решим систему уравнений

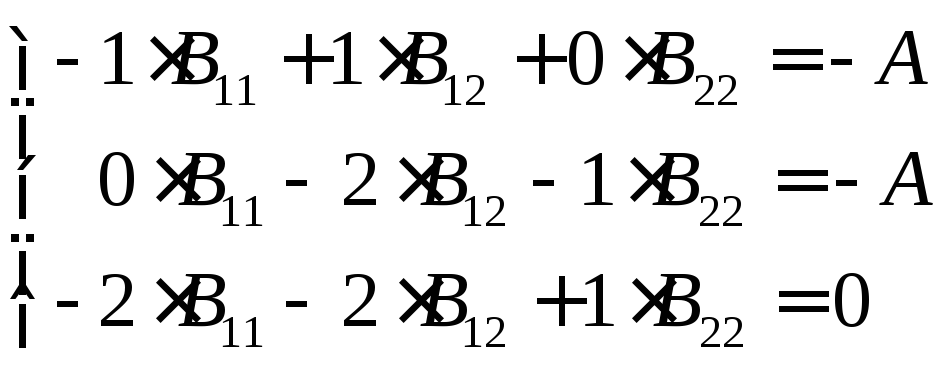
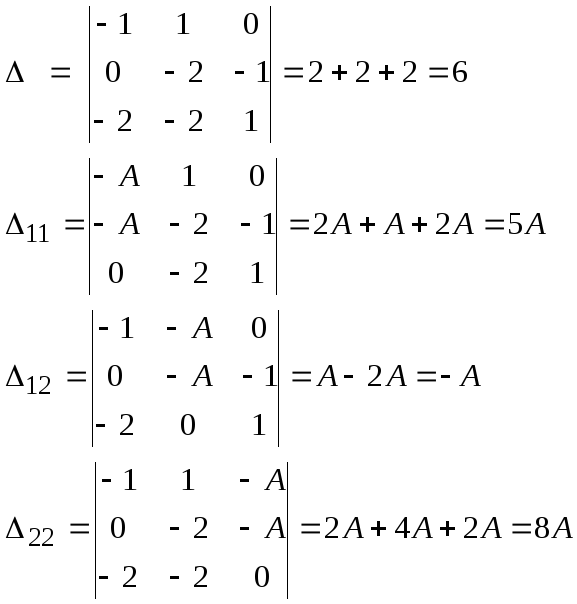(7.3.16)

(7.3.17)

(7.3.18)

При

В случае нелинейных систем единая методика выбора функции Ляпунова отсутствует, однако для систем отдельных типов имеются рекомендации по выбору функции Ляпунова. Например, для системы вида:

Рис. 7.3.1

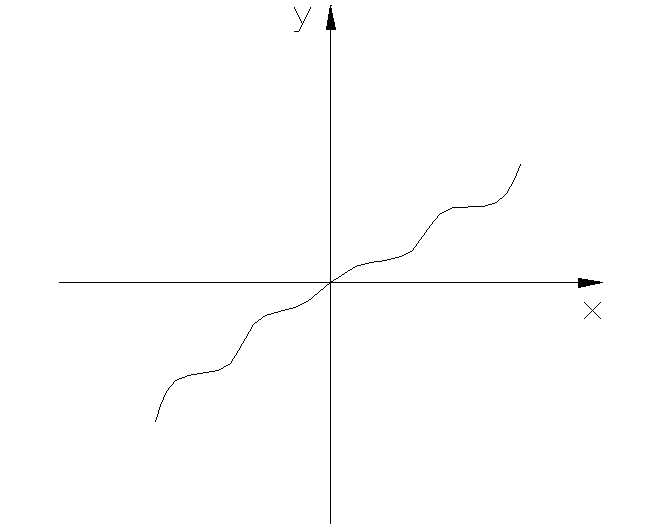
с характеристикой (рис.7.3.2) НЭ, удовлетворяющей условиям

f(0)=0,

А.И. Лурье и В.М. Постниковым был предложен следующий подход: функция Ляпунова находится как квадратичная форма от координат системы плюс интеграл от нелинейности

Рис. 7.3.2

β – постоянные коэффициенты (7.3.19)

Можно показать, что поверхности постоянных значений V=const, взятых в такой форме, содержат внутри себя начало координат и имеют значения d, возрастающие по модулю по мере удаления от начала координат. Эти поверхности заполняют все фазовое пространство и при соответствующем выборе значений и могут служить для определения устойчивости равновесия системы в целом (и в «малом», и в «большом»).

Пример: проверить устойчивость равновесия в системе

Линейная часть описывается выражением

.(7.3.20)

Н

(7.3.21)

(7.3.22)

(7.3.23)

(7.3.24)

айдем дифференциальное уравнение системы

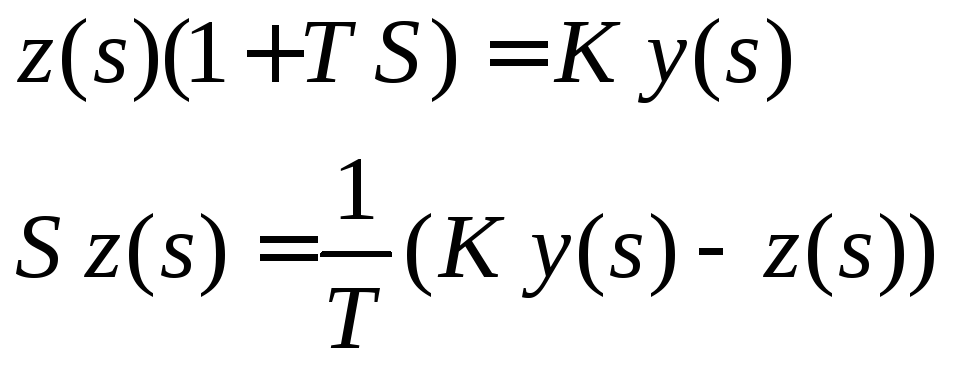
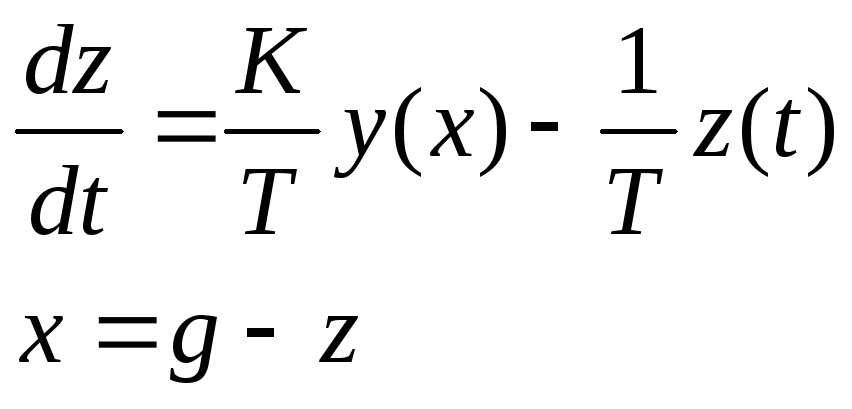
При определении устойчивости положения равновесия внешние воздействия должны отсутствовать, следовательно входной сигнал g=0, поэтому .

Дифференциальное уравнение нелинейной системы

. (7.3.25)

Функцию Ляпунова V выбираем в виде квадратичной формы плюс интеграл от нелинейности

(7.3.26)

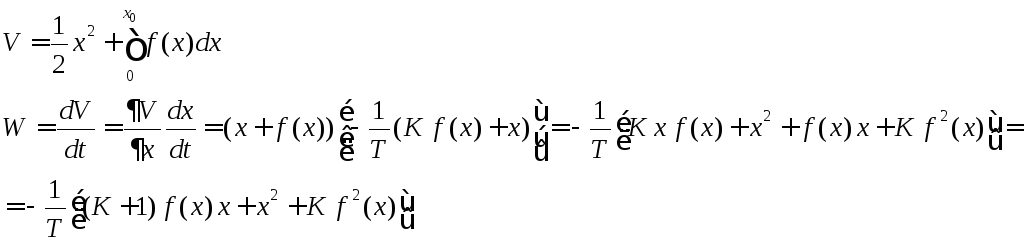
Если нелинейная характеристика проходит через первый и третий квадранты , то . При определённо положительной функции Ляпунова из (7.3.26) следует, что – функция определенно отрицательная при, что и является условием устойчивости.