
- •Теория автоматического управления теория нелинейных автоматических систем
- •Глава1. Виды и особенности нелинейных систем
- •1.1. Типовые нелинейные характеристики
- •1.2. Фазовое пространство и фазовая плоскость
- •1 .3. Типы особых точек и фазовые траектории линейных систем
- •1 .4. Особые линии в нелинейных системах
- •Глава 2. Фазовая плоскость систем, описываемых уравнениями с неаналитической правой частью
- •2 .1. Исследование системы со скользящим режимом
- •2 .2. Исследование релейной системы
- •2 .3. Многолистное фазовое пространство
- •4 .3. Алгебраический метод определения симметричных автоколебаний и их устойчивости
- •4 .4. Частотный метод определения автоколебательных режимов и их устойчивости (метод Гольдфарба л.С.)
- •4 .5. Учет временного запаздывания в нелинейной системе
- •Автоколебательных режимов.
- •2 -Ой метод:
- •4 .7 Несимметричные автоколебания в нелинейных системах.
- •4 .7.1 Гармоническая линеаризация нелинейностей
- •4.7.2 Определение периодических режимов при несимметричных колебаниях
- •6.1. Выбор корректирующих устройств, препятствующих возникновению автоколебаний в нелинейных системах
- •6 .1.1. Выбор линейных последовательных корректирующих устройств
- •(Местных обратных связей)
- •6 .2. Системы с переменной структурой (спс)
- •6.3. Исследование системы с переменной структурой методом фазовой плоскости
- •6 .4. Псевдолинейная коррекция
- •Глава 7. Исследование устойчивости нелинейных систем.
- •7.1. Устойчивость нелинейных систем. Функции Ляпунова а.М.
- •7.2. Теоремы Ляпунова (прямого метода Ляпунова)
- •7.3. Выбор функций Ляпунова
- •7.4. Частотный критерий абсолютной устойчивости
- •7.5. Сравнение методов анализа устойчивости нелинейных систем
- •Глава 8. Исследование устойчивости переходных процессов в нелинейных системах.
- •8.1. Абсолютная устойчивость процессов в нелинейной системе
7.5. Сравнение методов анализа устойчивости нелинейных систем
Рассмотрим область устойчивости (рис.7.5.1) на плоскости обобщённых параметров α, β нелинейной системы. Из рассмотренных методов анализа устойчивости нелинейных систем только с помощью метода фазового пространства можно найти точную границу устойчивости. Этот метод позволяет найти как необходимое, так и достаточное условие устойчивости.
Прямой метод Ляпунова и частотный критерий абсолютной устойчивости В.М. Попова позволяют найти только достаточное, но не необходимое условие устойчивости. При этом области устойчивости (1 и 2) получаются меньше, чем действительная граница, но эти методы гарантируют устойчивость этих в областях (1 и 2). В общем случае метод Ляпунова дает более узкую область достаточных условий, чем метод В.М. Попова. Метод гармонической линеаризации в зависимости от степени выполнения условия фильтра дает приближенное значение области устойчивости, однако, он не гарантирует устойчивость в данной области. Т.е. построенная с помощью метода гармонической линеаризации область устойчивости (3) может быть шире, чем в действительности.
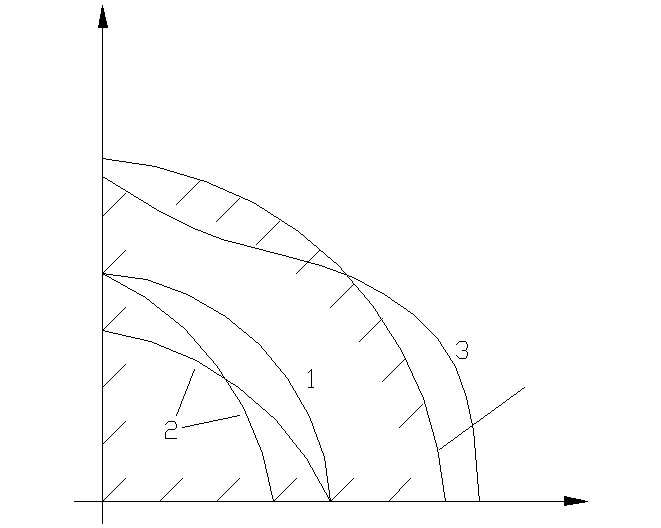
Нанести параметры α, β
1 – граница по методу В.М. Попова
2 – граница по методу Ляпунова
3
Д.Г.У.
Д.Г.У. – действительная граница
устойчивости
Рис. 7.5.1
Глава 8. Исследование устойчивости переходных процессов в нелинейных системах.
8.1. Абсолютная устойчивость процессов в нелинейной системе
f(x)
W(S) g


- - -








r
r




Рис. 8.1.1
Выполнение в нелинейной системе (рис.8.1.1) только условий абсолютной устойчивости положений равновесия может не обеспечивать абсолютной устойчивости процессов, вызванных каким-либо ограниченным по модулю воздействием g(t).
Б.Н. Наумовым и Я.З. Цыпкиным был предложен критерий абсолютной устойчивости процесса в системе с однозначной нелинейностью.
Основные положения:
1.
Для абсолютной устойчивости процессов
в системе с одной однозначной нелинейностью
достаточно, чтобы при заданном
![]() преобразованная передаточная функция
линейной части
преобразованная передаточная функция
линейной части ![]() была устойчива,
частотная характеристика W(jω)
при всех
была устойчива,
частотная характеристика W(jω)
при всех ![]() удовлетворяла бы
условию
удовлетворяла бы
условию 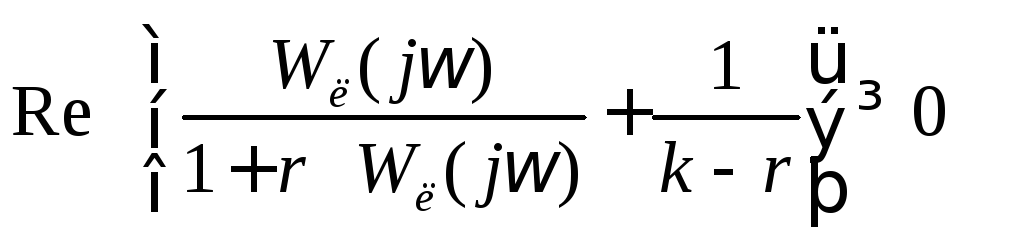 . (8.1.1)
. (8.1.1)
2. Нелинейная однозначная характеристика должна отвечать условию :
![]() (8.1.2)
(8.1.2)
Т.е.
производная нелинейной характеристики
(крутизна ![]() )
должна лежать в секторе (r,
k).
)
должна лежать в секторе (r,
k).
В
![]() или к виду
или к виду ![]() (8.1.4)
(8.1.4)
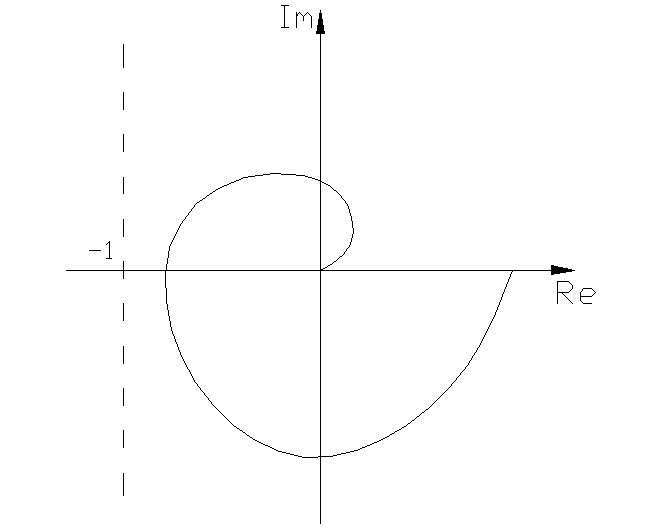
Из условия (8.1.4)
следует, что процессы будут абсолютно
устойчивы, если АФХ ![]() расположена правее
прямой
расположена правее
прямой
![]()
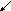
![]()
![]()
П
Рис. 8.1.2![]() .
Введем в рассмотрение параметр
.
Введем в рассмотрение параметр ![]() .С учетом этого выражение (8.1.1)
запишем в виде :
.С учетом этого выражение (8.1.1)
запишем в виде :
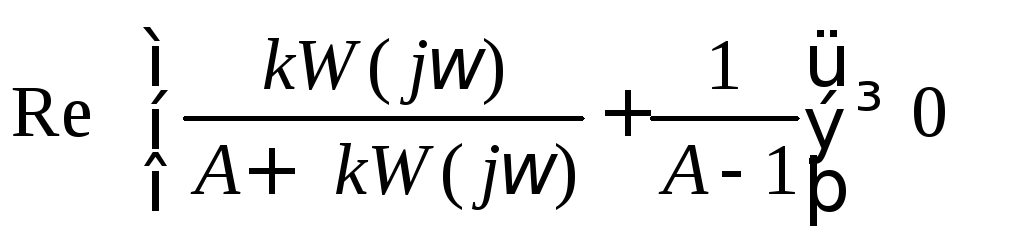 (8.1.5)
(8.1.5)
![]() (8.1.6)
(8.1.6)
Найдем
на комплексной плоскости ![]() и
и![]() геометрическое место точек, соответствующее
постоянным значениям A=const.
Для этого заменим в выражении (8.1.5) знак
неравенства на знак равенства. Затем,
подставляя выражение (8.1.6) в выражение
(8.1.5), прибавив и отняв
геометрическое место точек, соответствующее
постоянным значениям A=const.
Для этого заменим в выражении (8.1.5) знак
неравенства на знак равенства. Затем,
подставляя выражение (8.1.6) в выражение
(8.1.5), прибавив и отняв ![]() ,
выделив действительную часть и приравняв
ее к нулю, получим:
,
выделив действительную часть и приравняв
ее к нулю, получим:
![]() (8.1.7)
(8.1.7)
Выражение (8.1.7)
описывает семейство окружностей с
радиусом ![]() ,
проходящих через точку с координатами
,
проходящих через точку с координатами
![]() и лежащих левее прямой
и лежащих левее прямой ![]() (семейство
А-окружностей).
(семейство
А-окружностей).
Нанести точки А1 А2 А3
jkV
С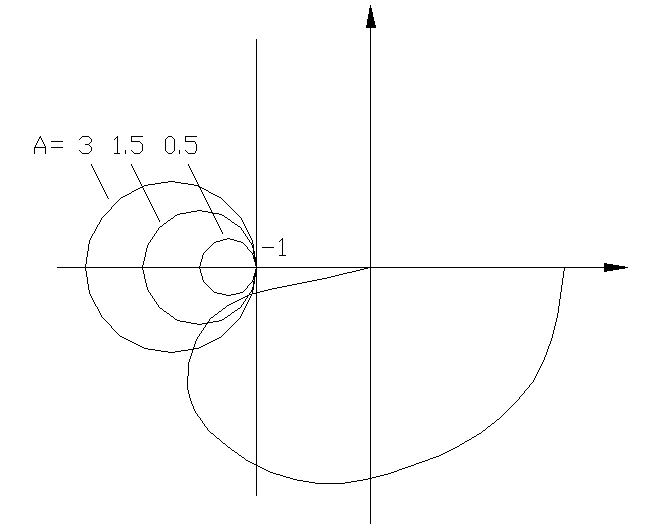
![]()
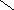 истема
обладает абсолютной устойчивостью.
истема
обладает абсолютной устойчивостью.
Д
kU - А1 - А2 - А3![]()
![]()
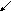
![]() ,
удовлетворяя критерию Найквиста, не
пересекала бы соответствующие
A-окружности.
,
удовлетворяя критерию Найквиста, не
пересекала бы соответствующие
A-окружности.
П
Рис. 8.1.3![]()
![]() и А-окружность переходит в
прямую линию (окружность бесконечного
радиуса.
и А-окружность переходит в
прямую линию (окружность бесконечного
радиуса.
Исследование абсолютной устойчивости процессов по ЛЧХ
(логарифмический критерий абсолютной устойчивости)
Рассмотрим систему
с устойчивой линейной частью и
нелинейностью, отвечающей условию
![]() .
(8.2.1)
.
(8.2.1)
Условие абсолютной устойчивости имеет вид:
![]() (8.2.2)
(8.2.2)
Частотные характеристики линейной части представим в виде:
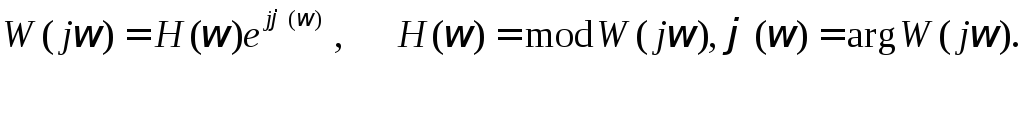 (8.3.3)
(8.3.3)
Условие (8.2.2) с учетом (8.3.3) можно заменить равноценным условием
![]() (8.2.4)
(8.2.4)
Условие (8.2.4)
автоматически выполняется в диапазоне
частот, где ![]() ,
поэтому необходимо исследовать систему
лишь при значениях
,
поэтому необходимо исследовать систему
лишь при значениях
![]()
![]() (8.2.5)
(8.2.5)
Следовательно вместо условия (8.2.4) можно потребовать выполнения равносильного ему условия:
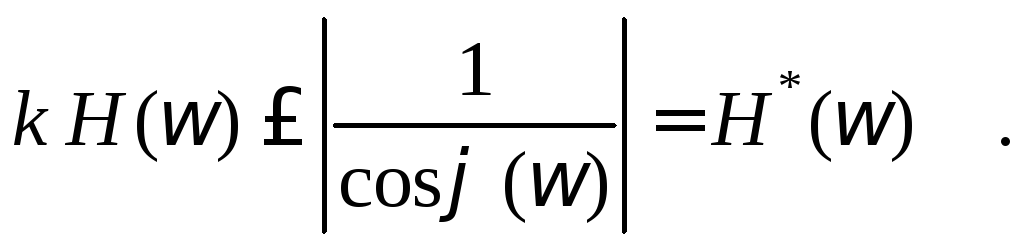 (8.2.6)
(8.2.6)
Если перейти к логарифмическим характеристикам, получим:
![]() (8.2.7)
(8.2.7)
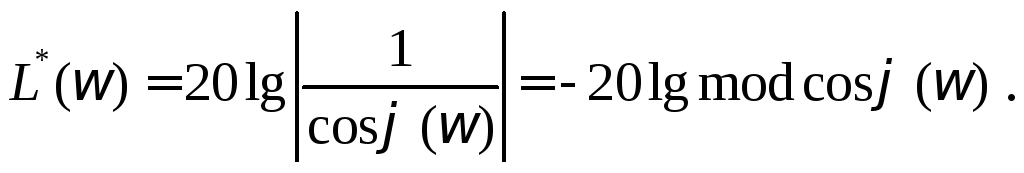 (8.2.8)
(8.2.8)
![]() –логарифмическая
характеристика критического коэффициента
передачи H*(ω).
–логарифмическая
характеристика критического коэффициента
передачи H*(ω).
Формулировка
критерия:
При ограниченном возмущении g(t)
и нелинейной характеристике, удовлетворяющей
условию (8.2.1), для абсолютной устойчивости
процессов в системе достаточно, если в
диапазоне частот, где выполняется
условие (8.2.5), нормированная ЛАХ
![]() не пересекает ЛАХ критического
коэффициента передачи
не пересекает ЛАХ критического
коэффициента передачи
![]() ,
т.е. условие устойчивости кратко можно
представить:
,
т.е. условие устойчивости кратко можно
представить:
![]()
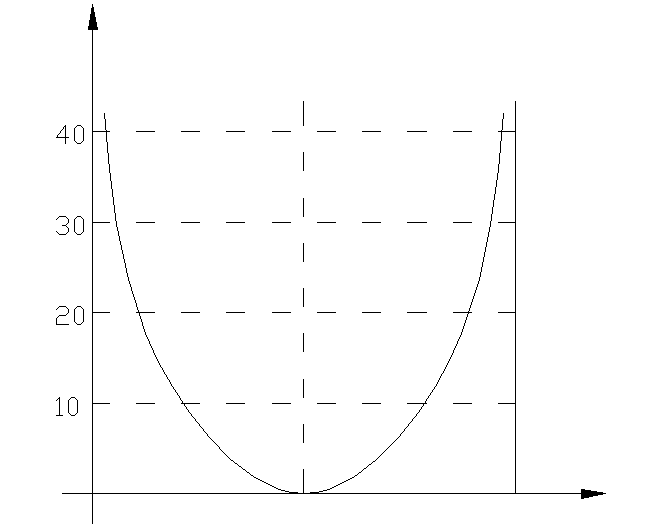
При
практическом использовании ЛАХ
![]() обычно строят
(рис. 8.2.1) в диапазоне углов:
обычно строят
(рис. 8.2.1) в диапазоне углов:
![]() по формуле (8.2.8).
по формуле (8.2.8).
При
углах меньших ![]() и больших
и больших ![]() условие (8.2.4) выполняется автоматически
и проверки не требует..
условие (8.2.4) выполняется автоматически
и проверки не требует..
![]()
![]()
![]()
Рис. 8.2.1![]()
![]()
Рис. 8.2.2![]()
По характеристикам
![]() и
и ![]() можно определить величину смещения ,
обеспечивающую абсолютную устойчивость
процесса.
можно определить величину смещения ,
обеспечивающую абсолютную устойчивость
процесса.
Если
обозначить через K
коэффициент передачи линейной части в
точке касания ![]() и
и ![]() ,
то
,
то ![]() .
.
![]()
Пример
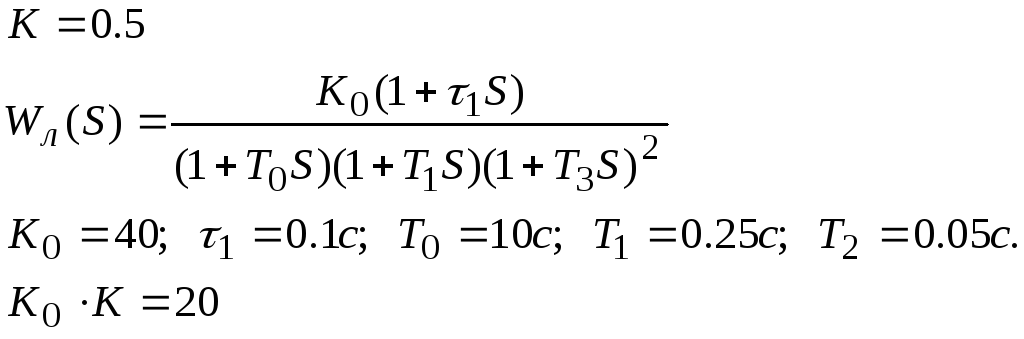 (8.2.11)
(8.2.11)
20 1 10 0.1 L=20
lg э 40 10 100 Lкр() L() -1 -2 -1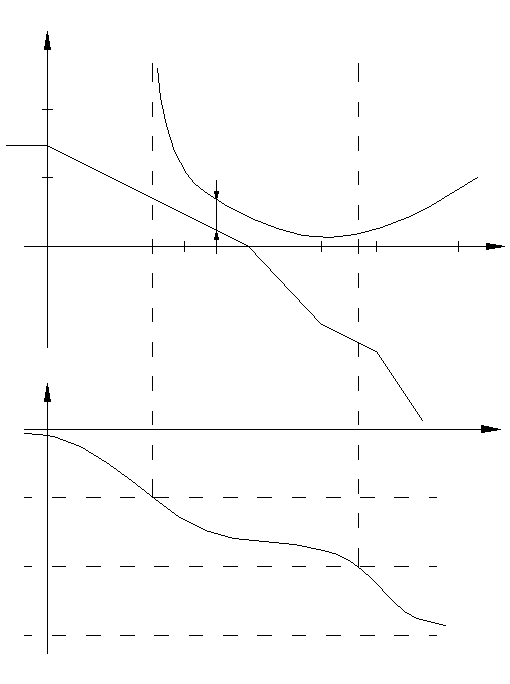
() -3 Рис. 8.2.3![]()
![]()
![]()
Условие
устойчивости выполняется. K
можно еще увеличить на ![]() ,
чтобы увеличить быстродействие и
точность.
,
чтобы увеличить быстродействие и
точность.
