
- •Теория автоматического управления теория нелинейных автоматических систем
- •Глава1. Виды и особенности нелинейных систем
- •1.1. Типовые нелинейные характеристики
- •1.2. Фазовое пространство и фазовая плоскость
- •1 .3. Типы особых точек и фазовые траектории линейных систем
- •1 .4. Особые линии в нелинейных системах
- •Глава 2. Фазовая плоскость систем, описываемых уравнениями с неаналитической правой частью
- •2 .1. Исследование системы со скользящим режимом
- •2 .2. Исследование релейной системы
- •2 .3. Многолистное фазовое пространство
- •4 .3. Алгебраический метод определения симметричных автоколебаний и их устойчивости
- •4 .4. Частотный метод определения автоколебательных режимов и их устойчивости (метод Гольдфарба л.С.)
- •4 .5. Учет временного запаздывания в нелинейной системе
- •Автоколебательных режимов.
- •2 -Ой метод:
- •4 .7 Несимметричные автоколебания в нелинейных системах.
- •4 .7.1 Гармоническая линеаризация нелинейностей
- •4.7.2 Определение периодических режимов при несимметричных колебаниях
- •6.1. Выбор корректирующих устройств, препятствующих возникновению автоколебаний в нелинейных системах
- •6 .1.1. Выбор линейных последовательных корректирующих устройств
- •(Местных обратных связей)
- •6 .2. Системы с переменной структурой (спс)
- •6.3. Исследование системы с переменной структурой методом фазовой плоскости
- •6 .4. Псевдолинейная коррекция
- •Глава 7. Исследование устойчивости нелинейных систем.
- •7.1. Устойчивость нелинейных систем. Функции Ляпунова а.М.
- •7.2. Теоремы Ляпунова (прямого метода Ляпунова)
- •7.3. Выбор функций Ляпунова
- •7.4. Частотный критерий абсолютной устойчивости
- •7.5. Сравнение методов анализа устойчивости нелинейных систем
- •Глава 8. Исследование устойчивости переходных процессов в нелинейных системах.
- •8.1. Абсолютная устойчивость процессов в нелинейной системе
6 .4. Псевдолинейная коррекция
Псевдолинейными называют такие нелинейные КУ, у которых эквивалентная передаточная функция, а значит, и коэффициенты гармонической линеаризации зависят только от частоты и не зависят от амплитуды колебаний. Однако, эта зависимость нелинейна в том смысле, что характер ее отличается от частотной зависимости линейных передаточных функций и может быть произвольным, т.е. отсутствует жесткая взаимосвязь между амплитудными и фазовыми характеристиками, которая есть у линейных звеньев. Это достоинство псевдолинейных устройств позволяет корректировать фазовые характеристики независимо от амплитудных и наоборот, что невозможно сделать линейными средствами.
Результат гармонической линеаризации псевдолинейного устройства y=f(x) имеет вид
![]() , (6.4.1)
, (6.4.1)
где
![]() – эквивалентная
ПФ псевдолинейного КУ (6.4.2)
– эквивалентная
ПФ псевдолинейного КУ (6.4.2)
Е.И. Хлыпало предложил форму представления псевдолинейного устройства в виде эквивалентного инерционного звена
![]()
Если
![]() ,
тогда
,
тогда
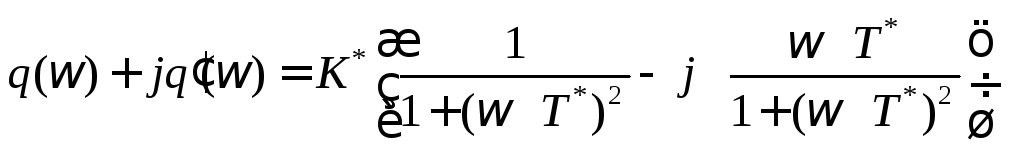 .(6.4.3)
.(6.4.3)
Приравнивая действительные и мнимые части в (6.3.3), получим
![]() (6.4.4)
(6.4.4)
После преобразований
![]() ,
,
получим
![]() (6.4.5)
(6.4.5)
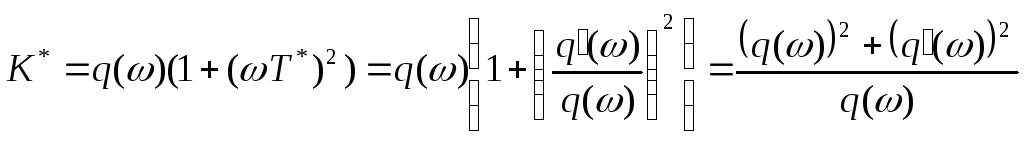 . (6.4.6)
. (6.4.6)
В
Цель коррекции – уменьшение инерционности, т.е. уменьшение фазового отставания выходного сигнала от входного. Частотные характеристики апериодического звена имеют вид:
K.Э. U
С.А.З. Апериодическое звено U1 U2







С.А.З. – схема анализа знаков.
З
Рис. 6.4.1
ПФ формирующих устройств: WK1=1+Ts, WK2=1.
При несовпадении знаков сигналов U1 и U2 ключ размыкается и при этом отсекаются хвостовые части выходного сигнала U (рис.6.4.2).
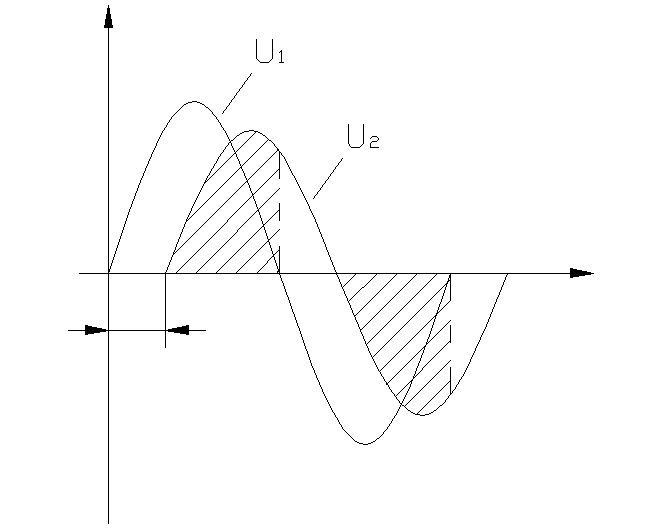
Рис. 6.4.2
Произведем гармоническую линеаризацию нелинейности (рис.6.4.3).
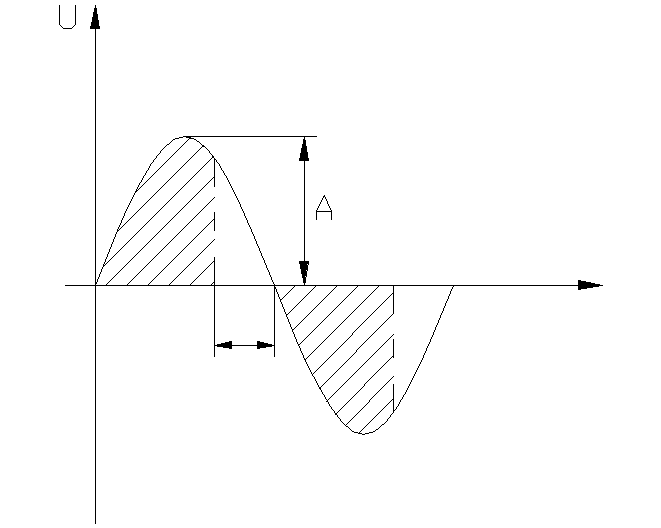
U
t
Рис. 6.4.3
Вычисление коэффициентов гармонической линеаризации.
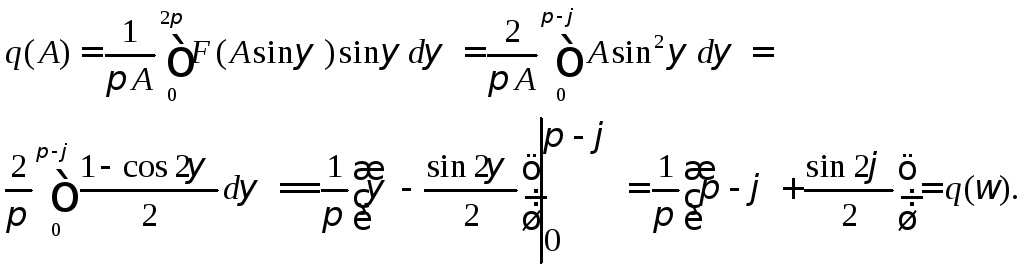 (6.4.7)
(6.4.7)
 (6.4.8)
(6.4.8)
Из выражений (6.4.7, 6.4.8) видно, что коэффициенты гармонической линеаризации являются функцией фазового сдвига φ(ω), следовательно частоты ω, и не зависят от амплитуды колебаний.
Эквивалентная передаточная функция всего устройства имеет вид
![]() (6.4.9)
(6.4.9)
Рассуждая аналогично предыдущему, найдем параметры Кэ и Тэ.
(6.4.10)
(6.4.11)
(6.4.12)
(6.4.13)
(6.4.14)
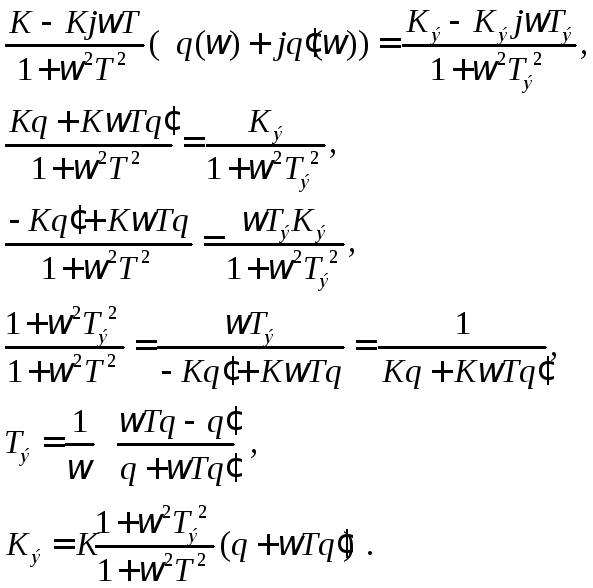
Вместо
![]() подставим его значение из (6.3.14) и получим
подставим его значение из (6.3.14) и получим
![]() (6.4.15)
(6.4.15)
![]()
![]()
П о
формулам (6.4.14, 6.4.15) были рас-считаны
относительные значения Кэ
и Тэ.
о
формулам (6.4.14, 6.4.15) были рас-считаны
относительные значения Кэ
и Тэ.

И
Рис.
6.3.3![]()
![]()
Глава 7. Исследование устойчивости нелинейных систем.
7.1. Устойчивость нелинейных систем. Функции Ляпунова а.М.
Уравнение динамики системы n-го порядка при отсутствии внешних воздействий в общем случае описывается следующей системой дифференциальных уравнений в нормальной форме Коши:
![]() . (7.1.1)
. (7.1.1)
где уi – координаты системы, а Fi – нелинейные функции.
Устойчивость
рассматривается как свойство свободного
движения системы, вызванного ненулевыми
начальными условиями. Решение системы
(7.11) представляет собой невозмущенное
движение ![]() .
При изменении начальных условий в
системе возникает возмущенное движение.
Отклонение возмущенного движения
.
При изменении начальных условий в
системе возникает возмущенное движение.
Отклонение возмущенного движения ![]() от невозмущённого,
определяемого уравнениями системы
(7.1.1) при определенных начальных условиях
от невозмущённого,
определяемого уравнениями системы
(7.1.1) при определенных начальных условиях
![]() ,
обозначим через
,
обозначим через ![]()
![]() (7.1.2)
(7.1.2)
Тогда уравнение возмущенного движения системы в отклонениях описывается системой дифференциальных уравнений
![]() - описывает движение
системы. (7.1.3)
- описывает движение
системы. (7.1.3)
При этом невозмущенным движением будет x* = 0.
![]()
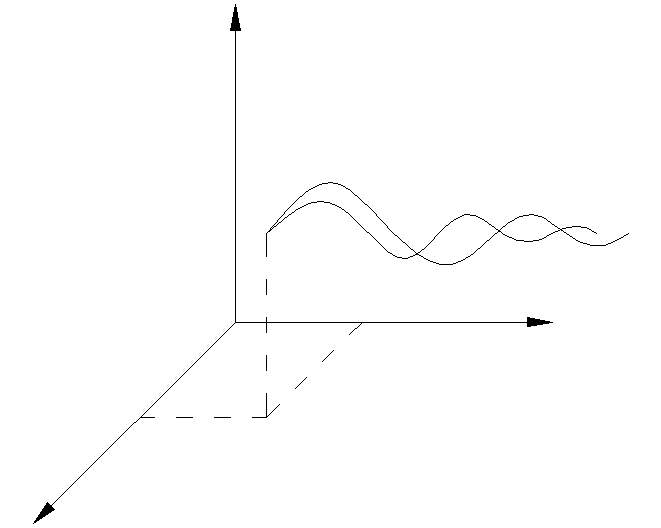 - координаты
состояния системы.
- координаты
состояния системы.
Г x*(t) () x2,…,xn
 еометрические
представления движений показаны на
рис.7.1.1.
еометрические
представления движений показаны на
рис.7.1.1.
y2,…,yn y1 t t0 y*(t) t x(t)
t0 Рис. 7.1.1 x1

Устойчивость по
Ляпунову: невозмущенное движение
![]() называется устойчивым, если задав трубку
сколь угодно малого сечения,
можно в начальный момент времени t0
подобрать такую область начальных
значений ,
зависящую от ,
что при увеличении времени
называется устойчивым, если задав трубку
сколь угодно малого сечения,
можно в начальный момент времени t0
подобрать такую область начальных
значений ,
зависящую от ,
что при увеличении времени
![]() возмущенное движениеx(t)
не выйдет из трубки сечением ,
т.е. при выполнении условия (7.1.4) выполнится
условие (7.1.5).
возмущенное движениеx(t)
не выйдет из трубки сечением ,
т.е. при выполнении условия (7.1.4) выполнится
условие (7.1.5).

Если при выполнении условия (7.1.4) выполняется (7.1.6), то движение называется асимптотически устойчивым.
Если условие (7.1.6) выполняется при выполнении условия (7.1.7), т.е. при любых начальных отклонениях, движение называют асимптотически устойчивым в целом.
Для нелинейных систем введено понятие абсолютной устойчивости. Под ней понимают асимптотическую устойчивость в целом при любой форме нелинейной характеристики внутри заданного класса нелинейности.
kx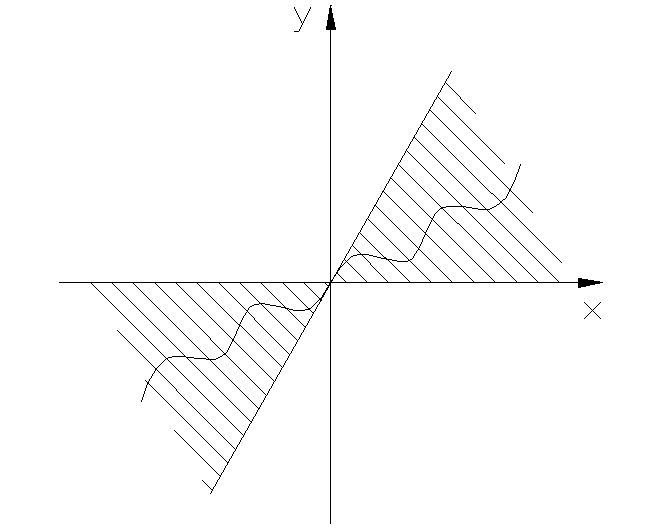
f(x) x
y


В
дальнейшем мы будем рассматривать
следующий класс нелинейных характеристик![]()
На нелинейность (рис.7.1.2) накладываются следующие ограничения:
–
Рис. 7.1.2
![]()
– нелинейная характеристика должна лежать внутри сектора [0,k]
![]() . (7.1.8)
. (7.1.8)
Внутри этого сектора она может иметь любой вид.
Понятие функции Ляпунова и ее производная.
В общем случае нелинейная система описывается системой дифференциальных уравнений:
![]() ,
(7.1.9)
,
(7.1.9)
где хi – отклонения координат системы от их значений в установившемся режиме
![]() –нелинейные и
произвольные функции, но отвечающие
одному требованию:
–нелинейные и
произвольные функции, но отвечающие
одному требованию:
![]() , т.е. они проходят через начало координат.
, т.е. они проходят через начало координат.
Функцией Ляпунова
называют функцию типа ![]() (7.1.10)
(7.1.10)
– это любая функция,
если в ней в качестве аргументов х1,
…, хn
приняты координаты состояния системы
– переменные из уравнения (7.1.9), и эта
функция ![]() при
при ![]() .
.
К функции Ляпунова применимы понятия знакоопределенности и знакопостоянства.
Знакоопределенной в некоторой области вокруг начала координат называют функцию, которая в любой точке в этой области принимает значение только одного знака и равна нулю только в начале координат.
Знакопостоянной называется функция, которая в указанной области принимает значения одного знака или нулевые.
![]() - знакоопределенная
(определенно положительная функция)
- знакоопределенная
(определенно положительная функция) ![]() - знакопостоянная (постоянно
положительная) Производная от функции
Ляпунова по времени имеет вид:
- знакопостоянная (постоянно
положительная) Производная от функции
Ляпунова по времени имеет вид:
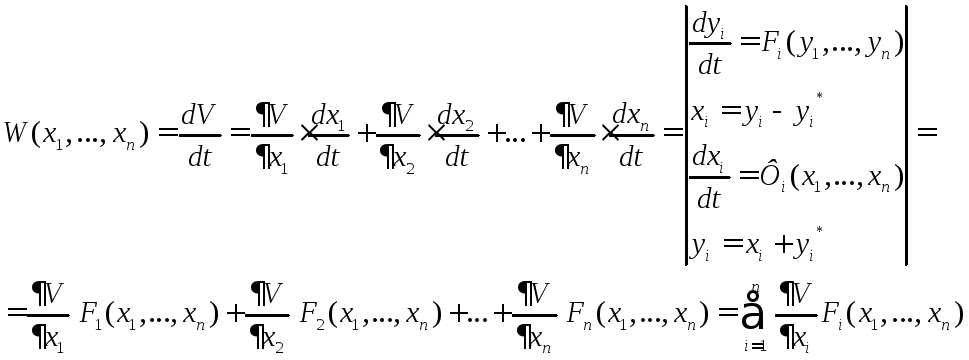 (7.1.11)
(7.1.11)
Производная функции Ляпунова, также как и сама функция Ляпунова, является некоторой функцией отклонений xi и обращается в нуль в начале координат, поэтому к производной W также как и к самой функции Ляпунова V могут быть применены понятия знакоопределенности и знакопостоянства в некоторой области вблизи начала координат.
