
Matematika_Zaytsev_ch2
.pdf
|α( x ) f ( x ) |=|α( x ) | | f ( x ) |< Mε M = ε ,
а это, согласно определению б.м., означает, что α(x) f(x) – б.м. Так как б.м. функция при x→ a ограничена в U o( a ) , то из теоремы 5 вытекает следствие.
Следствие. Произведение функций, б.м. при x→ a, есть снова б.м. при x→ a.
Функцию f(x) называют бесконечно большой (б.б.) при x → a , если при этом стремлении аргумента функция имеет бесконечный предел, т.е.
f(x) – б.б. при x→ a : lim f ( x ) =∞.
x→a
Замечание. Никакое постоянное число, как бы велико оно ни было по абсолют-
ному значению, не является б.б. функцией. |
|
|
|
|
||||||||||||
Пример 11. Доказать, что |
|
|
|
|
|
|
|
|
||||||||
а) f ( x ) = |
1 |
б.б. функция при x → 0; |
б) f(x) = x б.б. функция при x → ∞. |
|||||||||||||
|
||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• Возьмем произвольное E > 0. |
|
|
|
|
1 |
|
1 |
|
||||||||
|
1 |
|
> E , т.е. |
|
x |
|
< |
. Если взять δ = |
|
|||||||
а) Предположим, что |
|
|
|
, то по определе- |
||||||||||||
|
|
|
||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
E |
E |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
нию 8 следует, что lim |
1 |
= ∞ , т.е. |
1 |
|
|
– б.б. функция при x → 0. |
|
|||||||||
x |
x |
|
|
|||||||||||||
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|||
б) Для функции f(x)= x по определению 9 | f ( x )|> E E >0 при |x| >M=E. •
Связь между б.б. и б.м. функциями устанавливает следующая теорема.
Теорема 6. Если f(x) – б.б. функция при x→ a, тогда |
1 |
|
– б.м. при x→ a. |
|
f ( x ) |
||||
|
|
|||
Если α(x) – б.м. функция при x→ a, отличная от нуля в некоторой окрестностиU o( a ) точки a, то α(1x ) – б.б. функция при x→ a.
Доказательство. Пусть f(x) – б.б. функция при x→ a. По определению б.б.
функции при произвольном |
E = |
1 |
> 0 существует такая окрестностьU o( a ) точ- |
||||||||||||
ε |
|||||||||||||||
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|||
|
o |
|
|
|
|
|
|
|
|
|
0 |
||||
ки a, что x U |
|
( a ) |
| f ( x )| > E = |
|
. Тогда |
|
|
< ε |
x U (a), т.е. по |
||||||
|
ε |
| f ( x )| |
|
||||||||||||
определению функция |
1 |
|
|
– б.м. при x → a. |
|
|
|
|
|||||||
f ( x ) |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
71 |
|
|
|
|
|||
Если α(x) – б.м. при x→ a и α(x) ≠ 0 в некоторой окрестности U o( a ) точки a, то, согласно определению б.м.,
|
|
ε = |
1 |
> 0 U1o( a ) : x U o( a ) IU1o( a ) |α( x ) | < ε = |
1 |
, |
||||||
|
|
E |
E |
|||||||||
|
1 |
|
|
|
|
1 |
|
|
|
|||
т.е. |
|
|
> E , а это означает, по определению, что |
|
– б.б. при x→ a. |
|||||||
|α( x )| |
α( x ) |
|||||||||||
|
|
|
|
|
|
|
||||||
72

Приведём несколько достаточно очевидных и полезных на практике свойств б.м. и б.б. функций.
1)Произведение функций, б.б. при x → a, есть функция, б.б. при x → a.
Например, функция xn, n N – б.б. при x→ ∞.
2)Произведение функции, б.б. при x→ a, и функции, имеющей в точке конечный ненулевой предел, будет б.б. функцией при x→ a.
Например, функция x12 2x – б.б. при x→ 0.
3) Сумма ограниченной в некоторой окрестности U o( a ) точки a функции и б.б. функции при x→ a есть функция б.б. при x→ a.
Например, x + sinx, x + 1x – б.б. при x→ ∞.
4) Сумма двух функций, б.б. при x→ a, есть неопределённость вида (∞+∞). В зависимости от знака слагаемых характер изменения такой суммы может быть различным.
Например, |
f1(x) = x, f2(х) = 2x, |
f3(x) = – x – б.б. функции при x→ ∞, а |
|||||||||||||
f1(x) + f2(x) = 3x – б.б. при x→ ∞, |
f1(x) + f3(x) = 0 – б.м. при x → ∞. |
||||||||||||||
5) Пусть α1(x), α2(x) |
– б.м. при x→ a; f1(x), f2(x) – б.б. при x→ a; |
||||||||||||||
lim g( x ) = 1 . Тогда при x→ a функции |
|
|
|
|
|
|
|
||||||||
x→a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α1 ( x ) , |
|
f1 ( x ) |
, α1 ( x ) f1 ( x ), g( x ) f1 ( x ) , α1 ( x )α2 ( x ) , f1 ( x )α1 ( x ) |
||||||||||||
|
|
||||||||||||||
α2 ( x ) |
f2 ( x ) |
|
|
|
|
|
|
|
|
|
|
||||
есть неопределённости соответственно вида |
|
|
|
|
|
|
|
||||||||
|
|
0 |
|
∞ |
|
∞ |
|
|
0 |
|
0 |
|
|||
|
|
|
|
, |
|
, (0 ∞), (1 |
|
), |
(0 |
|
), |
(∞ |
). |
||
|
|
|
|
|
|||||||||||
|
|
0 |
|
∞ |
|
|
|
|
|
|
|
|
|||
При вычислении пределов таких функций при x→ a нужно применять специальные приёмы раскрытия таких неопределённостей. Об этом пойдёт речь позже.
2.2 Основные теоремы о пределах
Рассмотрим основные теоремы о пределах.
Теорема 7 (об единственности предела).
Если существует предел функции при х→ а, то он единственный.
Доказательство. Применим метод доказательства от противного. Допустим, что при х→ а функция f(x) имеет два предела b1 и b2, причем b1 ≠ b2. Тогда на основании теоремы 3 можем представить функцию f(x) в двух видах:
f(x) = b1 + α1(x) и f(x) = b2 + α2(x),
72
где α1(x) и α2(x) – б.м. функции при х→ а. Отсюда имеем b1 + α1(x) = b2 + α2(x) или α1(x) – α2(x) = b2 – b1. В левой части этого равенства – б.м. функция, а в правой – постоянная величина, не равная нулю. Мы пришли к противоречию, допустив наличие различных пределов у функции. Это доказывает теорему.
Теорема 8 (о пределе суммы, произведения и частного).
Если существуют конечные пределы функций f(x) и g(x) при х→ а, то существуют и пределы их суммы, произведения, частного и они равны соответственно сумме, произведению, частному пределов этих функций, т.е. справедливы ут-
верждения: ( lim = b1 |
) ( lim = b2 ) |
|
||||
x→a |
|
x→a |
|
|
|
|
lim( f ( x ) + g( x )) = b1 + b2 ; |
(15) |
|||||
|
x→a |
|
|
|
|
|
lim( f ( x )g( x )) = b1b2 ; |
(16) |
|||||
|
x→a |
|
b1 |
|
|
|
lim |
f ( x ) |
= |
, ( b ≠ 0 ) . |
(17) |
||
|
|
|||||
|
x→a g( x ) |
2 |
|
|||
|
|
b2 |
|
|||
Доказательство. По теореме 3 |
f(x) = b1 + α(x) и g(x) = b2 + β(x), |
где α(x) и |
||||
β(x) – б.м. функции при х→ а. Проведем доказательство только утверждения (16), а (15) и (17) рекомендуем доказать читателю самостоятельно.
Имеем
f ( x )g( x ) = ( b1 +α( x ))( b2 + β( x )) = b1b2 +α( x )b2 + β( x )b1 +α( x )β( x ) .
Сумма последних трёх слагаемых в правой части этого равенства в силу теорем 4 и 5 является б.м. при х→ а, что, согласно теореме 3, означает справедливость (16).
Ясно, что (15) и (16) можно распространить на произвольное конечное число слагаемых и сомножителей.
Следствия.
1) При вычислении предела функции постоянный сомножитель С можно выносить за символ предела, т. е. lim ( C f ( x )) = C lim f ( x ) .
|
x→a |
x→a |
2) lim |
( f ( x ))n = ( lim f ( x ))n , |
n Z. |
x→a |
x→a |
|
Теорема 9 (о переходе к пределу в неравенстве).
Если f(x) < g(x) при х→ а и существуют пределы этих функций, то
lim f ( x ) ≤ lim g( x ) .
x→a x→a
Доказательство. Т.к. lim |
f ( x ) и lim g( x ) , то lim ( f ( x ) − g( x )) = b . |
|
x→a |
x→a |
x→a |
Если предположить, что b > 0, тогда |f(x) – g(x) – b| > b из-за того, что
f(x) – g(x)< 0. Но это противоречит условию |f(x) – g(x) – b| < ε, которое должно выполняться для любого сколь угодно малого ε > 0 согласно определению 2. Итак,
73
число b ≤ 0, поэтому lim ( f ( x ) − g( x )) ≤ 0 или |
lim f ( x ) ≤ lim g( x ) , что и |
|
x→a |
x→a |
x→a |
требовалось доказать. |
|
|
Следствие. Если при х→ а справедливо f(x) > 0 (соответственно f(x) < 0) и
lim f ( x ) = b , то b ≥ 0 (соответственно b ≤ 0).
x→a
Теорема 10 (“принцип двух милиционеров”).
Пусть f(x), g(x), h(x) - три функции такие, что f(x) ≤ g(x) ≤ h(x) и пусть функции f(x) и h(x) имеют одинаковый конечный предел b при х→ а. Тогда функция g(x) имеет тот же предел при х→ а.
Доказательство. По условию теоремы с учётом определения предела существуют ε > 0 окрестности U1o( a ) и U2o ( a ) точки а, такие, что
| f ( x ) − b |< ε x U1o( a ) и | h( x ) − b |< ε x U2o( a ) .
Ясно, что x U1o( a ) IU2o ( a ) b −ε < f ( x ) < b + ε и b −ε < h( x ) < b + ε , или b −ε < f ( x ) ≤ g( x ) ≤ h( x ) < b + ε .
Отсюда следует |g(x) – b| < ε, что и доказывает теорему.
Теорема 11 (предел сложной функции).
Если функция y = f(x) имеет в точке а конечный предел b, причём f ( x ) ≠ b в
некоторой окрестности точки а, а функция g(y) имеет в точке b конечный предел с, то сложная функция g(f(x)) имеет предел в точке а и он равен с.
Доказательство. Из существования lim g( y ) = c следует, что
y→b
ε > 0 δ( ε ) > 0 : | g( y ) −c |<ε при |y – b| < δ.
Из существования lim f ( x ) = b следует, что для этого δ найдётся
x→a
δ1 > 0 : 0 < |x – a| < δ1 0 < |f(x) – b| < δ.
Следовательно, для таких x справедливо условие |g(f(x)) – с| < ε, а это означа-
ет, что lim g( f ( x )) = c .
x→a
Замечание. Эту теорему можно распространить на суперпозицию более двух функций. Она позволяет использовать замену переменной при вычислении пределов сложных функций по формуле
lim g( f ( x )) = lim g( y ) ,
x→a |
y→b |
при выполнении условий теоремы 11. При этом говорят, что сделана замена
y = f(x). Теорема 11 и возможность замены переменных остаются в силе, если хотя бы одна из точек a, b, с будет соответствовать одной из бесконечно удалённых точек +∞ или –∞ (или их объединению ∞).
74
Пример 12.
замену y = x12
|
|
|
|
|
|
|
1 |
|
при х → 0 сделаем |
||
Для нахождения предела функции arctg |
|
|
|
|
|||||||
|
x |
2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
||
. Тогда при х→ 0 |
следует y→ +∞ и |
|
|
|
|
|
|
||||
lim arctg |
|
1 |
|
lim |
arctgy = |
π |
. |
|
|
|
|
|
|
= |
|
|
|
|
|
||||
x2 |
2 |
|
|
|
|||||||
x→0 |
|
|
y→+∞ |
|
|
|
|
|
|||
2.3 Два замечательных предела
Замечательными (из-за большого числа их приложений) называются пределы
|
sin x |
|
|
1 |
|
|
|
||
функций y = |
|
и y = ( 1 + x ) |
x |
при х → 0. |
|||||
x |
|||||||||
|
|
|
|
|
|
|
|||
1. Докажем, что |
|
sin x |
|
|
|||||
|
|
|
lim |
= 1 |
(первый замечательный предел). (18) |
||||
|
|
|
|
x |
|||||
|
|
|
x→0 |
|
|
|
|||
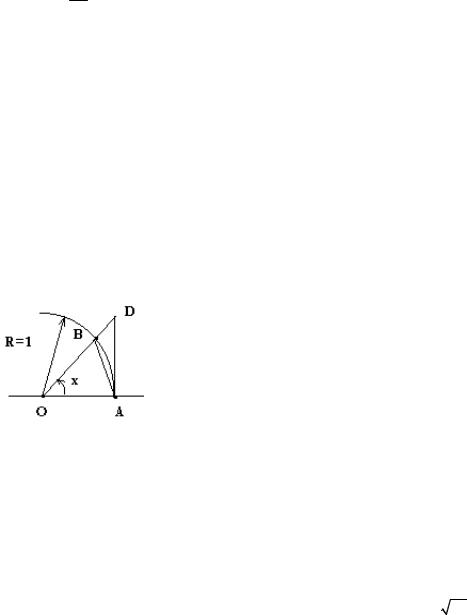
Доказательство. Пусть х – центральный угол окружности единичного радиуса
(рисунок 7), причем 0 < x < π . Из сравнения площадей S1 треугольника OАB, S2 |
|||||||
|
2 |
|
|
|
|
|
|
сектора АОB и |
S3 треугольника OАD следует S1 < S2 < S3. При |
OА = ОB = 1 |
|||||
|
имеем S1 = 0,5 sinx, S2 = 0,5 x, S3 = 0,5 tgx, поэтому |
||||||
|
|
π |
sinx < x < tgx. |
Ясно, что |
|||
|
x 0, |
|
|||||
|
|
2 |
|
|
|
|
|
|
|
|
|sinx| ≤ |x| |
|
x R. |
(19) |
|
|
|
|
|
0, |
π |
|
|
|
Действительно, при x |
2 |
справедливость следует |
||||
|
|
|
|
|
|
|
|
Рисунок 7 |
из левой части предыдущего двойного неравенства. |
||||||
При x ≥ π справедливость очевидна из условия |sinx| ≤ 1. |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
При x < 0 справедливость следует из нечетности sinx и определения модуля. |
|||||||
При x = 0 имеем случай равенства. |
|
|
|
|
|
|
|
Из (19) следует |
|
|
|
|
|
|
|
lim sin x = 0 и lim cos x = 1 . |
|
|
|
|
|
(20) |
|
x→0 |
x→0 |
|
|
|
|
|
|
В самом деле, в силу неравенств |sinx – 0| < |x| и |cosx – 1| = |
2 sin |
2 |
x |
≤ |
x2 |
в |
|
|
2 |
2 |
|||||
|
|
|
|
|
|
||
определении 2 достаточно положить δ = ε для первого предела в (20) и δ = 2ε для второго. Вернёмся к двойному неравенству, которое можно записать в виде:
75
|
sin x |
|
|
π |
|
π |
\{0}. |
||
cos x < |
|
< 1 x |
− |
|
, |
|
|
||
x |
2 |
2 |
|||||||
|
|
|
|
|
|
||||
Таким образом, функция sinx x заключена между двумя функциями, имеющи-
ми при x→ 0 одинаковый предел, равный 1. Поэтому по теореме 10 получим (18).
Замечание. В силу теоремы 11 первый замечательный предел можно записать в более общей форме:
lim
α( x )→0
Пример 13. Вычислить пределы
а) |
lim |
tgx |
; |
|
б) |
lim |
sinax |
||||
|
|
x |
|||||||||
|
x→0 |
x |
|
|
x→0 |
||||||
• а) lim |
|
tgx |
= lim |
sin x |
|
|
1 |
||||
|
|
|
|
|
|
|
|
||||
|
x |
x |
|
|
|
||||||
x→0 |
|
x→0 |
|
|
|
cos x |
|||||
sinα( x ) = |
1 . |
|
|
|
||||
α( x ) |
|
|
|
|
|
|||
; в) lim |
1 − cos ax |
, a ≠ 0 R . |
||||||
|
|
|
||||||
|
x→0 |
|
x2 |
|
|
|||
|
lim |
sin x |
|
|
1 |
|
|
|
= |
x→0 |
x |
|
= |
= 1 ; |
|||
lim cos x |
|
|
||||||
|
1 |
|
|
|||||
x→0
б) lim |
sinax |
= lim a sinax |
= |
y = ax |
= a lim sin y |
= a ; |
||
x→0 |
x |
x→0 |
ax |
|
y →0 при x → 0 |
y→0 |
y |
|
|
|
1 −cos ax |
|
|
|
|
2 sin |
2 ax |
|
ax |
|
|
2 y |
|
|
|
|
||||||||
в) lim |
|
= lim |
2 |
= |
2 |
= y x = a |
= |
|
|
||||||||||||||||
|
|
|
x2 |
|
|
|
|
|
|
|
|||||||||||||||
x→0 |
|
|
|
|
|
|
x→0 |
|
x2 |
|
y →0 при x →0 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2a |
2 |
sin |
2 |
y |
|
a |
2 |
|
|
|
sin y |
2 |
|
a |
2 |
|
sin y |
2 |
|
a |
2 |
|
||
= lim |
|
|
= |
|
|
lim |
|
|
= |
|
lim |
|
= |
|
. • |
||||||||||
|
|
4 y2 |
|
|
|
|
|
|
y |
|
|
y |
|
|
|||||||||||
y→0 |
|
|
|
|
|
2 |
|
y→0 |
|
|
2 |
y→0 |
|
2 |
|
||||||||||
2. Выпишем второй замечательный предел
1 |
|
|
|
lim ( 1 + x ) |
x |
= e = 2,71828 K |
(21) |
x→0 |
|
||
Число е является иррациональным числом. В курсе высшей математики важное значение имеют экспонента ех и натуральный логарифм ln x = loge x .
На первый взгляд результат в (21) довольно неожиданный: 1 + x → 1 при x→ 0, а единица в любой степени есть единица! Но из-за того, что показатель сте-
пени 1x при x→ 0 является б.б. функцией, а основание степени все же не единица,
хотя и отличается от нее при x→ 0 на б.м. функцию, предел не равен единице.
76

|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
Приведём значения функции |
y( x ) = ( 1 + x ) |
x |
|
при стремлении x к нулю. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x |
1 |
1 |
|
1 |
|
|
1 |
|
0,1 |
|
0,01 |
0,001 |
0,0001 |
|||||
|
|
|
2 |
|
|
3 |
|
|
|
4 |
|
|
|
|
|
|
|
|
y(x) |
2 |
2,250 |
2,370 |
|
2,441 |
2,534 |
|
2,7047 |
2,7169 |
2,7181 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство (21) в данном пособии не приводится. Второй замечательный
предел позволяет, как говорят, «раскрыть» неопределённость типа (1∞). Используя теорему 11, предел можно записать в более общей форме:
1 |
|
lim ( 1 +α( x ))α( x ) = e . |
(22) |
α( x )→0
Второй замечательный предел имеет широкое применение. С его помощью находятся многие другие пределы.
|
|
|
|
|
|
|
|
|
3 |
x |
|
|
||||
Пример 14. |
Найти |
lim |
1 |
+ |
|
|
|
. |
|
|
||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
x→∞ |
|
|
|
|
x |
|
|
||||
• Положим |
|
3 |
=α или x = |
|
3 |
|
. Тогда при x→ ∞ |
|||||||||
|
x |
α |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
3 x |
|
|
|
|
|
|
|
3 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
тельно, lim 1 |
+ |
|
|
= lim ( 1 +α )α = lim ( 1 |
+α |
|||||||||||
|
||||||||||||||||
x→∞ |
|
|
x |
α→0 |
|
|
|
|
|
|
|
|
|
α→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
следует α→ 0. Следова-
1 3
)α = e3 . •
3. ПОНЯТИЕ НЕПРЕРЫВНОСТИ ФУНКЦИИ
3.1 Определения непрерывности
Рассмотрим функцию f(x), определённую, по крайней мере, в некоторой окрестности U(a) точки a, так что в этой точке функция имеет определённое значение f(а). При введении понятия предела функции в точке а было подчеркнуто, что эта точка может и не принадлежать области определения функции, а если и принадлежит, то значение f(а) не играет никакой роли. При введении понятия непрерывности функции в точке её значение в этой точке играет решающую роль.
Определение 13. Функцию f(x) называют непрерывной в точке a, если в этой точке существует конечный предел функции и он совпадает с её значением f(а),
т.е. если
( lim |
f ( x )) ( lim f ( x ) = f ( a )) . |
(23) |
x→a |
x→a |
|
Замечание. Условие (23) можно еще записать следующим образом:
lim f ( x ) = f ( lim x ),
x→a |
x→a |
т. е. под знаком непрерывной функции можно переходить к пределу.
77
Если раскрыть содержание этого определения на языке ε – δ, то можно сформулировать эквивалентное ему определение.
Определение14. Функцию f(x) называют непрерывной в точке a, если
ε > 0 δ(ε) > 0 : ( |x – a| < δ |f(x) – f(a)| < ε ). |
(24) |
Если сравнить условие (24) непрерывности функции в точке a с определением предела в этой точке, то видно, что различие состоит в замене значения b предела
на значение f(а) функции и в дополнении к проколотой δ – окрестности точки a самой этой точки.
Обратим внимание на существенную сторону определения непрерывности
функции на языке ε – δ. Это определение говорит о том, с какой точностью надо задавать значения аргумента функции для того, чтобы получить значения функции с заданной точностью. Именно эта практическая сущность данного определения
позволяет понять, почему так много внимания уделено изложению на языке ε – δ понятия предела и непрерывности.
Приведём еще одно определение непрерывности функции, которое по существу
является перефразировкой определения 13. Для этого lim f ( x ) = f ( a ) запи-
x→a
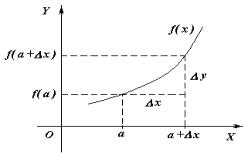
шем в равносильном виде lim ( f ( x ) − f ( a )) = 0 . Разность x – a называется
( x−a )→0
приращением аргумента x в точке a и
обозначается, как правило, ∆x , а раз-
ность f(x) – f(а) – приращением функ-
ции f(x) в точке a, вызванным приращением аргумента ∆x , и обозначается ∆y или ∆ f ( a ) . Таким образом,
∆x = x – a, ∆y = ∆ f ( a ) =
= f(x) – f(а) = f(a + ∆x ) – f(а).
Рисунок 8
Геометрический смысл приращений ясен из рисунка 8, на котором и ∆x и ∆y
положительны. В общем случае каждое из них может иметь любой знак. Используя новые обозначения, можно дать еще одно эквивалентное определе-
ние непрерывности функции.
Определение 15. Функцию f(x) называют непрерывной в точке a, если
lim ∆y = lim ∆ f ( a ) = 0 , |
(25) |
∆x→0 ∆x→0
т.е. б.м. приращению аргумента должно соответствовать б.м. приращение функции.
Это определение для практического использования бывает иногда более удобным, и им будем также пользоваться.
78
Пример 15. Показать непрерывность функций |
|
|
|||||||||||||||||
|
а) f(x) = c = const; |
б) f(x) = x; |
в) f(x) = sinx в каждой точке a R. |
||||||||||||||||
• |
х R можно записать: |
|
|
|
|
|
|
|
|
|
|
||||||||
а) |
∆ f ( x ) = f ( x + ∆x ) − f ( x ) = c − c ≡ 0 и выполнено условие (25); |
||||||||||||||||||
б) |
∆ f ( x ) = x + ∆x − x = ∆x , очевидно lim ∆x = 0 ; |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆x→0 |
|
|
|||
в) |
| ∆ f ( x )| = | sin( x + ∆x ) − sin x | = | 2 sin |
∆x |
|
∆x |
|||||||||||||||
2 |
cos x + |
| ≤ | ∆x | , |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
∆x |
|
|
|
|
|
∆x |
|
|
| ∆x | |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||||||||
так как |
|
cos x + |
|
|
≤ 1 , |
|
sin |
|
|
≤ |
|
|
|
. Поэтому (25) выполняется. • |
|||||
2 |
|
|
|||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
Определение 16. Функцию f(x) называют непрерывной слева (справа) в точке а, если в этой точке существует конечный левосторонний (правосторонний) предел функции и он совпадает с её значением f(а).
Если функция определена на отрезке [a, b], то по отношению к граничным точкам a и b можно говорить лишь о непрерывности функции справа в точке a или слева в точке b. Непрерывность функции в любой внутренней точке промежутка равносильна непрерывности функции в такой точке справа и слева, так как существование предела в точке равносильно существованию и равенству односторонних пределов в этой точке (см. теорему 2).
Итак, в точке a непрерывности функции f(x) должны быть выполнены все следующие условия:
1)функция определена в точке a и в некоторой её окрестности;
2)существуют оба односторонних предела функции в точке а и они конечны;
3)оба односторонних предела функции в точке a совпадают, т.е.
f(a – 0) = f(a + 0);
4) совпадающие односторонние пределы функции в точке a равны значению функции в этой точке, т.е.
f(a – 0) = f(a + 0) = f(a).
3.2 Точки разрыва
Функцию, не являющуюся непрерывной в точке a, называют разрывной в этой точке, а саму точку a – точкой разрыва этой функции.
Таким образом, функция будет разрывной в точке a, или, говорят, функция терпит разрыв в точке a, если будет нарушено хотя бы одно из условий 1) – 4) непрерывности функции в точке.
Классификация точек разрыва дается в зависимости от того, какие условия будут нарушены.
Точкой разрыва первого рода называют такую точку разрыва функции, в которой существуют оба односторонних предела этой функции и они конечны, т.е. выполнено, по крайней мере, условие 2 непрерывности функции в точке.
79
