Matematika_Zaytsev_ch2

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Алтайский государственный технический университет им. И.И.Ползунова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

f ( b ) − f ( a )

g(a) = a, g

x, то, согласно (1), получим

= f ( c ), т. е. (2).

.pdf

Скачиваний:

Добавлен:

14.02.2015

Размер:

2.17 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 2313 14 15 16 17 18 19 20 21 22 23 > Следующая >>>

( x3 )′ + (ln y)′ = ( x2e y )′ 3 x2 +

y′ = 2 x e y

+ x2 e y y′

x y (2e y − 3 x)

y′ − x2e y y′ = 2 xe y − 3 x2

y′ =

2 xe y − 3 x2

− x

1 − x2 ye y

Отсюда получим, что y / = 0 при x = 0 . ●

8. Найти производную 3-го порядка функции

y = 0,25 x2 (2 ln x − 3) .

● Последовательно вычисляем производные:

′

y′ = 0,25 ( x2 )

(2 ln x − 3) + x2 (2 ln x −

3)′

= 0,25

2 x

(

2 ln x − 3) + x2

= 0 ,25 (4 x ln x − 4 x) = x (ln x − 1) ;

y′′ =( y′)′ = x′(ln x −1) + x(ln x −1)′ = ln x −1+ x

= ln x ;

y′′′ =( y′′)′ =(ln x)′ =

.●

9. Найти yxx//

функции, заданной параметрически:

x = t − sin t

1 − cos t

y =

● Так как

xt/

= (t − sin t )′ = 1 − cos t ,

yt/

= (1 − cos t )′ = sin t , то, согласно (13),

yt/

sin t

2 sin

cos

= ctg

имеем: yx/

xt/

1 − cos t

2 sin

Используя формулу (30), получим:

−

ctg

sin

yxx//

t =

= −

. ●

1 − cos t

2 sin

4 sin

10. В какой точке графика функции

f ( x ) = ln x касательная параллельна

прямой y = x − 5 ? Записать уравнение касательной и нормали в этой точке. ● Исходим из уравнения касательной в точке касания ( x0 , f ( x0 )) :

y = f ′( x0 )( x − x0 ) + f ( x0 ) .

119

Для функции f ( x ) = ln x имеем f ′( x ) =	1	, поэтому	f ′( x0 ) =	1	– угловой
	x
				x0

коэффициент касательной. У прямой y = x − 5 угловой коэффициент равен 1. Так как касательная и прямая параллельны, то их угловые коэффициенты совпадают:

1	= 1 x = 1 ,	f ( x ) = ln1 = 0 . Итак, точка (1; 0) – точка касания, а

0		0
x0

уравнение касательной в этой точке имеет вид: y = 1 ( x −1 ) +0 = x −1 . Уравне-

ние нормали y = −

( x − x )+ f ( x

) , поэтому y = −1( x −1)+0 = −x +1 . ●

f ′( x0 )

f ( x ) = ln( x +

x2 + 1 ) при

11. Вычислить дифференциал df

функции

x =

3 .

● Согласно определению:

(

)

′

df =

f ( x )dx =

x +

dx =

x +

2 x

. Поэтому

df ( 3 ) = 0 ,5dx . ●

x2 + 1

6.2

Задачи для самостоятельного решения

1. Используя только определение производной, найти производные следующих

функций:				1
1)	f ( x ) = 10 x2 + x − 1 ;	2)	f ( x ) =	1	;
1)	f ( x ) = 10 x2 + x − 1 ;	2)	f ( x ) =	x	;
				x
3)	f ( x ) = sin 2 x ;	4)	f ( x ) =		1 + 2 x .

2. Исходя из определения производной, найти производные функций в указан-

ных точках:

1 − x

x ≤ 0

sin x , x ≤ 0

, x = 0

; 2)

x = 1 .

1) f ( x ) =

x , x > 0

f ( x ) =

x2 −

3 x + 2, x > 0

3. Найти производные следующих функций:

y = 2 x5 − x3 − 3 x + 4 ;

2) y = 3 x + 2 x3 −

+ 3 ;

y = log2 x − 2x + 3 arccos x ;

y = 5 sin x +

− arcctgx +

;

y = arctgx tgx ;

y = 3 x ln x + 2

x ;

120

y =

5 +

;

y =

2 cos x − sin x

− x2 lg x ;

5 −

e x

y =

x −

x ;

10)

y = cos3 ( 1 − x3 ) ;

11)

y = 101−x sin2 3 x ;

12)

y =

e5 x

;

x2 + 4

y = ln lg (2x + x2 ) ;

13)

14)

y = e

ln x

;

15)

y =

;

16)

y = lnarctg

1 + x2

;

x +

x2 + 1

17)

y = arcsin

sin 2 x ;

18)

y = e x 2 ctg 3 x ;

e 2 x

y = arctg ( x −

1 + x

) .

19)

y = ln

;

20)

2 x

+ 1

4. Вычислить производные функций в указанных точках:

y = sin3 2 x − cos3 2 x ,

= π ;

y =

x − 1 10

x = 0 ;

2 x

3) y = 3(3 x − 2 x ) , x0 = 1 ;

y =

1 − 10 x

, x0 = 0 .

10 x )ln10

5. Вычислить производные функций:

1 + 2 x , x ≤ 0

y =

2 x

;

y = arcsin

x > 0

6. Используя предварительное логарифмирование, найти производные следующих функций:

x ( x2 + 1)

tg3

y =

; 2) y = x3

x − 1

;

y =

ln x e

2 x

;

1 − x2

( x + 2) x − 2

3 1 − 2 x

5) y = x3 x 2x ;

ln2 x

y = (ln x )

;

y =

(cos x) x

7. Для функций, заданных параметрически, найти

yx/

в указанных точках:

x = t 2
		3	, t = 2 ;
1)	t
y =			− t
	3

	2t
x = e		, x = 1 ;
2)	−t	, x = 1 ;
y = e	−t

121

x = t ln t			t	cos t		π
	ln t , x = 0 ;	x = e		cos t	, t =	π	.
3)	ln t , x = 0 ;	4)			, t =	6	.
y =		y = et sin t
y =		y = et sin t
	t
	t

8. Для функций, заданных неявно, найти производные yx/ в указанных точках:


1)	x3 − 2 x2 y2 + 5 x + y − 5 = 0 , M ( 1; 1 ) ; 2) e y + xy = e , M ( 0;1 ) ;
3)	2 y = 4 + xy3 ,		M ( 1;−2 ) ;		4) y2 = x + ln	y	,	M ( 1;1 ) .

9. Найти производные функций xy/						x
				, обратных к заданным, в указанных точках:
	1)	y = x + e x , M ( 0; 1 ) ;		2)	y = x ln x , M( 1; 0 ) ;
	3)	y = 3 x + x2 , M ( 0;0 ) ;		4)	y = 2 + x − 0 ,5 sin x ,			M ( 0;2 ) .
10. Вычислить указанные производные высших порядков:
1) y = e2 x sin 3 x ,			y′′( 0 ) ;	2) y = ln( x − 1 ) , y′′′( 2 ) ;

	x = t	2
	x = t	, yxx// при t = 1 ;
3)		, yxx// при t = 1 ;
y = t 3		+ t

	x = ln(1	− t )
	x = ln(1	− t )	, y //	при t = 0 ;
4)			, y //	при t = 0 ;
y = t 2			xx

5) x − y + arctgy = 0 , y // при y = 1 ; 6) x4 − xy + y4 = 1, y′′в точке M ( 0;1 ) .

11. При каких значениях х касательные к графику функции y = x3 − x параллельны прямой y = x ?

12. Составить уравнения касательной и нормали к графику функции y = f ( x ) в данной точке ( x0 , f ( x0 )) , если:

1) y = x3 + 2 x2 − 4 x − 3 , x = −2 ;	2) y = e1−x2 , x = −1 .
0	0

13. Закон движения материальной точки по прямой имеет вид

S= 0,25t 4 − 4t 3 + 16t 2 .

1)Определить скорость движения в момент времени t = 1 .

2)В какие моменты времени скорость равна нулю?

3)Определить ускорение движения при t = 0 .

14. Записать дифференциалы функций при указанных значениях аргумента x0

и произвольном его приращении ∆x = dx :
1)	f ( x ) = sin x − xcos x + 4 , x = π ; 2) f ( x ) = x arctgx −ln 1+ x2		, x	= 3 .
	0	2	0
		2
	15. Найти дифференциалы указанных порядков от функций:
1)	f ( x ) = ln2 x −4 , d2 f ; 2) f ( x ) = sin2 x, d3 f ; 3) f ( x ) = xln x,			d5 f .
		122

Глава 5. ПРИЛОЖЕНИЯ ПРОИЗВОДНЫХ

В предыдущей главе мы познакомились с дифференцированием функции. Изучим теперь различные приложения понятия производной. Задача данной главы – применение производных для исследования различных свойств функции: будет ли она возрастающей или убывающей, имеет ли она экстремумы, каково её наибольшее и наименьшее значение и т.д. Полное исследование функции делает возможным построение схематического графика функции, наглядно представляющего поведение функции. Рассмотрим эти вопросы. Предварительно нам нужно рассмотреть некоторые весьма важные теоремы и формулы, которые будут использоваться в дальнейшем.

1. ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ

1.1 Теоремы о среднем

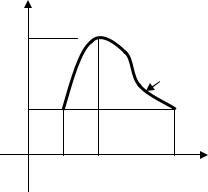
Теорема 1 (Ролля). Пусть функция f(x) непрерывна на отрезке [a,b] и дифференцируема на (a,b) (т.е. во всех его внутренних точках). Если f(a) = f(b), то най-

дётся точка c ( a,b ) :

f ′( c ) = 0.

Доказательство. Так как функция

y = f(x) непрерывна на [a,b], то на этом

отрезке данная

функция достигает наи-

меньшее значение m и наибольшее значе-

y= f(x)

ние М, т.е. имеем

x [ a,b ].

m ≤ f ( x ) ≤ M

Если m = M,

то f(x) = const, поэтому

f ′( x ) = 0 в любой точке. Если m ≠ M ,

то хотя бы одно из этих чисел отлично от

f(a) = f(b). Предположим, что M ≠ f (a ),

Рисунок 1

тогда существует c ( a,b ) : M = f(c)

(рисунок 1). В этом случае приращение

функции ∆ f = f ( c + ∆x ) − f ( c ) ≤ 0

для любого ∆x. Значит,

∆ f

≤ 0 при

∆ f

∆x

∆x > 0 и

≥ 0 при ∆x < 0 . Поэтому,

∆x

∆ f

∆ f ≥ 0.

f ′( c + 0 ) =

lim

≤ 0,

f ′( c − 0 ) =

lim

∆x→0+0

∆x

∆x→0−0

∆x

Так как функция дифференцируема в точке с, то f ′( c ) = 0, что и доказывает теорему.

123

Замечания.

1.В условиях теоремы Ролля на графике функции y = f(x) найдётся, по крайней мере, одна точка, в которой касательная параллельна оси OX (геометрический смысл теоремы Ролля ).

2.Нарушение хотя бы одного из условий теоремы Ролля может привести к тому, что производная не обратится в нуль ни в одной точке.

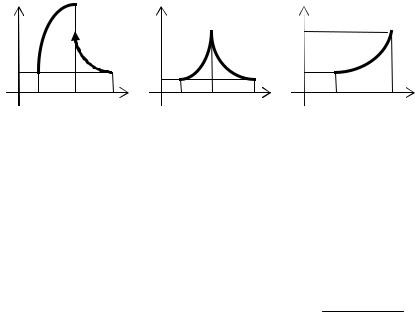
Приведём графические примеры. На рисунке 2 нарушена непрерывность на

[a,b]; на рисунке 3 нарушена дифференцируемость во внутренней точке; на рисунке 4 нарушено условие f(a) = f(b).

Y Y Y

0 a	b X	0 a	b X 0	a	b X
Рисунок 2		Рисунок 3			Рисунок 4

Теорема 2 (Коши). Пусть функции f(x) и g(x) непрерывны на [a,b], дифференцируемы на (a,b), причём g′( x ) ≠ 0 x ( a,b ). Тогда существует c ( a,b ) :

f ( b ) − f ( a )	=	f ′( c )	.	(1)
g( b ) − g( a )
		g′( c )

Доказательство. Рассмотрим вспомогательную функцию F(x) = f(x) − λg(x), где число λ подберём так, чтобы функция F(x) удовлетворяла условиям теоремы

Ролля. Условия непрерывности и дифференцируемости выполняются при любом λ, так как f(x) и g(x) обладают указанными свойствами. Условие F(a) = F(b) вы-

полнится, если f(a)− λg(a) = f(b)− λg(b), т.е. при λ = f ( b ) − f ( a ) . Заметим, g( b ) − g( a )

что g( b ) − g( a ) ≠ 0, так как иначе по теореме Ролля для функции g(x) будет g′( x ) = 0 в некоторой точке, что противоречит условию.

Применим к функции F(x) теорему Ролля:

′

f ( b ) − f ( a )

′

c ( a,b ) : F ( c ) = 0 f ( c ) −λg ( c ) = 0

f ( c ) − g( b ) − g( a )

g ( c ) = 0

f ( b ) − f ( a )

f ′( c )

, что и требовалось доказать.

g( b ) − g( a )

g′( c )

Теорема 3 (Лагранжа). Если функция f(x) непрерывна на [a,b], дифференцируе-

ма на (a,b), то c ( a,b ) :

f ( b ) − f ( a ) = f ′( c )( b − a ).

(2)

124

Доказательство. Применим теорему Коши для случая g(x) = x. Т. к. g(b) = b,

Замечания.

1. Равенство (2) называется формулой Лагранжа или формулой конечных при-

ращений (приращение аргумента b − a на отрезке [a,b] не бесконечно мало, как и

приращение функции f(b) − f(a) в общем случае). Эта формула имеет многообразное применение в математическом анализе.

2. Во всех трёх рассмотренных теоремах фигурирует под знаком производных некоторое среднее значение аргумента c ( a,b ), которое остаётся неизвестным.

В связи с этим обстоятельством все приведённые теоремы обычно называют тео-

ремами о среднем значении.

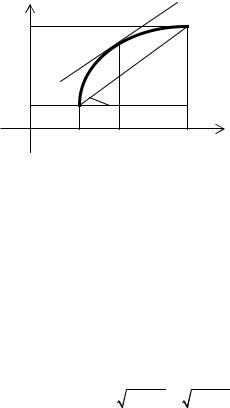
Y	y=f(x)	3. Имеется простой геометрический
		смысл теоремы Лагранжа (рисунок 5).
f(b)		Величина	f ( b ) − f ( a )	= tgα , где


			b − a
		α – угол наклона хорды, проведённой

αчерез точки (a, f(a)) и (b, f(b)). Так как

f(a)				f ′( c ) – тангенс угла наклона касатель-
0	a	c	b X	ной, то теорема Лагранжа фактически
0	a	c	b X	утверждает, что при указанных условиях
	Рисунок 5			на дуге графика функции всегда най-
				дётся хотя бы одна точка, в которой
касательная будет параллельна хорде, стягивающей концы дуги.
Следствие.		Если функция	f(x)	дифференцируема на (a,b) и x ( a,b )

f ′( x ) = 0, то f(x) = C – постоянная функция.

Доказательство. Возьмём любые x1 , x2 ( a,b ) : x1 < x2 . По теореме Ла-

гранжа c ( x1 , x2 ) : f ( x2 ) − f ( x1 ) = f ′( c ) ( x2 − x1 ). Т. к. f ′( c ) = 0 ,

то f(x1) = f(x2), поэтому значения функции во всех точках одинаковы.

Пример 1. Пусть f(x) = arcsinx + arccosx, x (–1; 1). Показать, что

	f ( x ) = π			x ( −1;1 ).
		2
● Так как f ′( x ) =	1	+	−1	= 0 x ( −1;1 ), то имеем f(x) = C.
	1 − x2		1 − x2

Определим эту постоянную величину С: C = f (0)=arcsin0 +arccos0 =0+π2 =π2 .

Итак, f ( x ) =	π	, т.е.	arcsin x + arccos x =	π	x ( −1;1 ). ●
	2			2
			125

1.2 Правило Лопиталя

В этом пункте рассмотрим способ раскрытия неопределённостей вида 0 и

∞ при помощи производных. Этот способ называют правилом Лопиталя.

∞

Теорема 4 (Лопиталя). Пусть выполнены следующие условия:

1) функции f(x), g(x) дифференцируемы в некоторой окрестности U( a ) точ-

ки x = a за исключением, быть может, самой точки; 2) g′( x ) ≠ 0 в U( a ) ;

3) lim	f ( x )	представляет собой неопределённость вида	0		или	∞	(т. е.
3) lim		представляет собой неопределённость вида			или		(т. е.
x→a g( x )				0		∞

функции f(x) и g(x) являются одновременно либо бесконечно малыми, либо бесконечно большими при x → a );

4) существует lim			f ′( x )	= A.
4) существует lim				= A.
	x→a		g′( x )
Тогда lim	f ( x )	существует и равен А.
Тогда lim		существует и равен А.
x→a	g( x )
Доказательство проведём только для случая неопределённости вида					0		:

						0
						0

lim f ( x ) = lim g( x ) = 0. Доопределим функции f(x) и g(x) в точке x = a, поло-

x→a x→a

жив их равными нулю, т. е. f(a) = g(a) = 0. Тогда функции будут непрерывными в окрестности U( a ) . Применим к этим функциям теорему Коши на отрезке [a,x]

(если x > a) или на отрезке [x,a] (если x < a), x U( a ) : с между a и x:

f ( x ) − f ( a )	=	f ( x )	=	f ′( c )	.
g( x ) − g( a )		g( x )
				g′( c )

Перейдём в последнем равенстве к пределу при x → a (тогда, очевидно, и c → a ):

lim	f ( x )	= lim	f ′( c )	= A.

x→a g( x )		c→a g′( c )

Замечания.

1.Теорема Лопиталя справедлива и для случая A = ±∞, так как конечность А нигде не использовалась.

2.Правило Лопиталя можно применять и при x → ±∞ . Для этого применим замену переменной и правило дифференцирования сложной функции:

126

′

−

f ′

f ( x )

y =

f ′( x )

lim

= lim

x→∞ g( x )

y →0

y→0 g

y→0

′

y→0 g′

x→∞ g′( x )

−

f ′( x )

3. Правило Лопиталя можно применять повторно, если производные

g′( x ) удовлетворяют тем же требованиям, что и сами функции f(x) и g(x).

Пример 2.

Вычислить lim

e−x − cos x

sin x

x→0

● Имеем неопределённость вида

, так как e−0 − cos 0 = 1 − 1 = 0 ,

sin0

Другие

условия

теоремы

Лопиталя

также

выполнены:

функции

f ( x ) = e−x − cos x

и g(x) = sinx дифференцируемы для всех x;

производная

g′( x ) = cos x ≠ 0

в окрестности x = 0;

предел отношения производных сущест-

вует и легко вычисляется:

lim

f ′( x )

= lim (e−x − cos x)′ = lim

−e−x + sin x = −1 + 0

= −1.

x→0

g′( x )

x→0

(sin x)′

x→0

cos x

Итак,

lim

e−x − cos x

= −1. ●

sin x

x→0

Пример 3.

Вычислить

lim

ln2 x

x→+∞

ln2

∞

2 ln x

ln x

∞

● lim

lim

= 2 lim

2 lim

x→+∞

∞

x→+∞

∞

x→+∞

= 2

lim

2 0 = 0.

●

x→+∞ x

Пример 4.

Вычислить

lim

x + sin x

x→∞

● Здесь правило Лопиталя неприменимо, так как

lim

( x + sin x)′

= lim

1 + cos x

= lim (1 + cos x) не существует. Попытка при-

x′

x→∞

менения привела бы к ошибочному выводу, что исходный предел не существует.

x + sin x

sin x

На самом деле lim

lim

= 1 + lim

= 1

+ 0

= 1.

●

x→∞

127

Неопределённости вида ( 0 ∞ ),		( ∞ − ∞ ),		( 1∞ ), ( 00 ), ( ∞0 ) предва-
рительно преобразуют к виду	0	или	∞	, после чего используют правило


	0		∞

Лопиталя.

Для неопределённостей ( 1∞ ), ( 00 ), ( ∞0 ) можно применять очевидное тождество

f ( x )g( x ) = eg( x )ln f ( x )

Покажем это на примерах.

Пример 5. Вычислить

lim ( 1 − x )tg

π x .

x→1

′

π x

1 − x

● lim ( 1 − x )tg

= ( 0 ∞ )

= lim

π x

π x ′

x→1

ctg

x→1

ctg

= lim

−1

. ●

x→1 −

2 π x

sin

Пример 6.	Вычислить	lim x x .
		x→0+0
● lim x x = ( 00 ) = lim		lim	( x ln x )	=
● lim x x = ( 00 ) = lim		e x ln x = ex→0 +0		=
x→0+0	x→0+0

	0 ∞		lim	ln x			∞
			lim	x−1			∞
( e		) = e	x→0 +0	x−1	=		∞	=
( e		) = e			=	e		=

	lim	x−1
	lim	−1 x−2
	= ex→0 +0	−1 x−2

lim	( −x )	= e0 = 1. ●
= ex →0 +0		= e0 = 1. ●

1.3 Формула Тейлора

Ставится задача: представить функцию f(x) в некоторой окрестности точки

x = a в виде многочлена относительно разности x − a (по степеням x − a) и найти ошибку такого приближённого представления.

Рассмотрим сначала простейшую из элементарных функций − многочлен степени n относительно x:

P(x) = a0 + a1x + a2x2 + a3x3 + ...+ anxn, где an≠ 0.

Здесь ai (i = 0, 1, 2, ..., n) − коэффициенты многочлена (заданные числа). Преобразуем этот многочлен в многочлен той же n-й степени, но уже относи-

тельно разности x − a , т.е. получим равенство:

P(x) = A0 + A1(x − a) + A2(x − a)2 + A3(x − a)3 + ... + An(x − a)n .

128

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 2313 14 15 16 17 18 19 20 21 22 23 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.02.20151.73 Mб316matem-up1.pdf
#
14.02.201554.78 Кб17Matematika-i-statistika-12-RiSO-B.doc
#
14.02.2015543.23 Кб30matematika_ekzamen - .doc
#
14.02.20152.69 Mб320matematika_metod_posobie.docx
#
14.02.20151.69 Mб232Matematika_ryad.doc
#
14.02.20152.17 Mб54Matematika_Zaytsev_ch2.pdf
#
14.02.20158.95 Mб92matematike_fepo_s_otvetami.doc
#
24.08.20193.22 Mб24materialoved.doc
#
14.02.2015899.5 Кб40mcad_pract.pdf
#
14.02.2015203.78 Кб25mech.doc
#
15.11.2019323.76 Кб7Meeting clients.docx