Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Алтайский государственный технический университет им. И.И.Ползунова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Matematika_Zaytsev_ch2

.pdf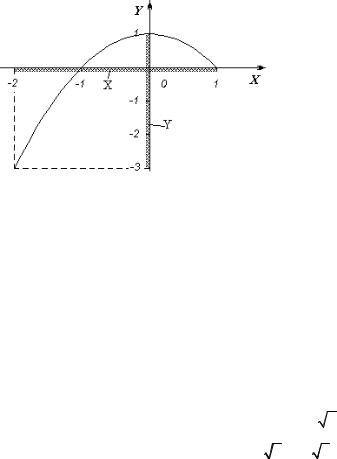

Скачиваний:

Добавлен:

14.02.2015

Размер:

2.17 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 236 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 > Следующая >>>

б) Область определения функции определяется неравенством sinx > 0, так как областью определения логарифмической функции являются положительные числа,

афункция sinx определена x R. Решая это неравенство, найдем, что

D(f) = {x R : sinx > 0} = {x R : 2nπ < x < (2n + 1)π, n Z}.

в) Область определения

D(f) = {x R: –1 ≤ 2 + x < 1} = {x R: –3 ≤ x < –1 } = [–3; –1). •

4. Найти множество Y , на которое данная функция y = f(x) отображает множе-

ство X:					x − 1
а) y = 1 – x2 ,	X = [–2; 1];		б)	y =	x − 1	, X = [ 1; 3 ] ;
а) y = 1 – x2 ,	X = [–2; 1];		б)	y =	x − 5	, X = [ 1; 3 ] ;
					x − 5
в) y = cos 2x ,		π
в) y = cos 2x ,	X = 0;	.
		4

• a) Функция y = 1 – x2 возрастает на промежутке [–2;0], при этом ее значения изменяются от y(–2)= –3 до y(0)=1, и убывает на промежутке (0;1], при этом ее значения изменяются от y(0)=1 до y(1)=0. Таким образом, Y=[–3; 1] (рисунок 15).

Рисунок 15

б) Множество X входит в естественную область определения функции и данная дробно–линейная функция будет убывающей (убедиться самостоятельно).

Так как y(1) = 0,	y(3) = – 1, то Y = [–1; 0].
в) При 0 ≤ x < π	будет 0 ≤ 2x < π , в этом случае косинус является моно-
4	2
тонно убывающей функцией. Таким образом, функция cos2x отображает X на
Y1 = (0;1], потому что cos0 = 1, cos π = 0. Монотонная функция		x отобразит
	2
множество Y1 в само множество Y1, т.е. Y = (0; 1], так как 0 = 0,		1 = 1 . •

	1		1	, если f ( x ) =	1	+ x
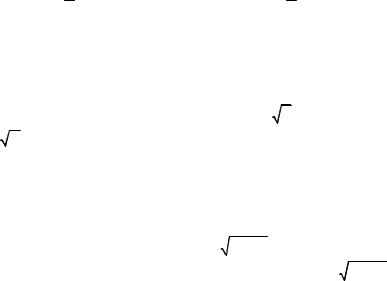
5. Найти f(0), f(2), f(–x), f(x–1), f(x) – 1, f		,					.
			f ( x )		1	− x
x

• f ( 0 ) =

1 +0

= 1 ;

f ( 2 ) =

1 + 2

= −3 ,

f ( −x )

1 +( −x )

1 − x

;

1 −0

1 − 2

1 −( −x ) 1 + x

f ( x −1 ) =

1 +( x −1 )

;

f ( x ) −1 =

1 + x

−1 =

;

2 − x

− x

1 −( x −1 )

1 − x

x + 1

1 + x −1

1 − x

;

•

−

x −1

f ( x )

1 − x

1 + x

6. Определить, какие из перечисленных функций имеют обратные. Найти соответствующие обратные функции и их области определения.

а) f(x) = 2x+1,		x R;	б) f(x) = (1 – x)3, x [–1, 3);
в) f(x) = x2 + 1,		x [–1, 2];	г) f ( x ) = 2x2 , x [0,2] ;
д) f ( x ) =	x + 1, x ( −∞, 0 ]

	2 x + 1, x ( 0, + ∞ ) .

• а) Функция y = f(x) = 2x + 1 монотонно возрастает x R, графиком является прямая линия с положительным угловым коэффициентом. Выразим x из ра-

венства y = 2x + 1: x = 21 ( y − 1 ). Таким образом, f −1 ( x ) = 21 ( x − 1 ) – обрат-

ная функция для данной функции (аргумент обратной функции обозначили привычной для аргумента буквой x). Очевидно, D(f –1) = R и обратная функция также монотонно возрастает.

б) Функция f(x) = (1 – x)3 монотонно убывает x R, в том числе и на мно-

жестве D(f ) = [–1; 3). Ясно, что E(f) = (–8; 8].

Выражая x из равенства y = (1 – x)3, получим x = 1 − 3 y . Таким образом, f −1 ( x ) = 1 − 3 x – обратная функция. Так как D(f–1) = E(f), то D(f –1) = (–8; 8].

в) Функция y = x2 + 1, x [–1; 2] не имеет обратной, так как на этом промежутке функция не монотонна (убывает при x [–1; 0] и возрастает при x (0; 2]).

г) Функция f ( x ) = 2x2 монотонно возрастает на отрезке [0; 2], поэтому су-

ществует обратная функция. Выразим x из равенства

y = 2x2 : x2 = log2 y x = log2 y.

Взят знак «+» перед квадратным корнем, так как x ≥ 0. Итак, f −1 ( x ) = log2 x

– обратная функция, а её область определения D(f –1) = E(f) = [1; 16], так как f(0) = 1, f(2) = 16.

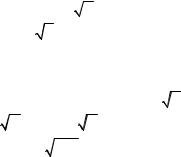
д) Исходная функция является составной, D(f) = R, E(f) = R, монотонно возрастает на R, поэтому существует обратная функция. Для её получения нужно обратить функции f1(x) = x + 1, D(f1)=(–∞; 0], E(f1)=(– ∞; 1] и f2(x) = 2x+1, D(f2) = (0; +∞), E(f2) = (1; +∞). Итак,

	x − 1,			x ( −∞; 1] ,
f −1		1		•
	( x ) =
			( x − 1 ) , x ( 1; + ∞ ) .
		2

7. Данные сложные функции записать в виде цепочки равенств, каждое звено которой содержит основную элементарную функцию:

а) y = (2x – 5)10;	б)	y = lntg	x	;

		2
в) y = 2cos 5 x ;	г)	y = arcsin( 3−x2 ).

• а) y = u10, где u = 2x – 5. Здесь y = u10 – степенная функция, а u = 2x – 5 – линейная функция.

б) Данную функцию можно представить в виде следующей цепочки:

y = ln u , u = tg v ,	v =	x	.
		2

Каждая из этих функций является основной элементарной: логарифмическая функция, функция тангенса, линейная функция.

в)	y = 2u , u = cosv, v = 5x (показательная, функция косинуса, линейная).
г)	y = arcsinu, u = 3v , v = – x2 (функция арксинуса, показательная, степен-
ная).•

8. Сложные функции, заданные цепью равенств, записать в виде одного равен-

ства:

а) y = u2 ,

u = sinv ,

v =

x ;

б) y = arctg u ,

u =

v , v = lgx;

в) y = 2u,

u ≤ 0

u = x2

– 1.

0 ,

u > 0

• а) Нужно подставить вместо v его значение

x , а затем заменить u в первом

неравенстве: y = (sin

x )2 = sin2

x .

б) Аналогично:

y = arctg

lg x .

в) Здесь нужно вместо u подставить выражение x2 – 1:

−1 ),

−1 ≤ 0

−1 ), x [ −1; 1]

2( x

•

y =

или y =

x [ −1; 1].

0 ,

−1 > 0

0 ,

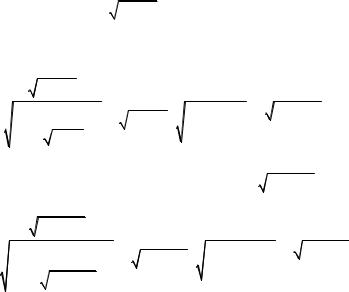
9. Составить f(f(x)), f(g(x)), g(f(x)), g(g(x)) и указать их области определения, где

	f ( x ) = 2x ,		g(x) = log2x.
• Сложная функция f(f(x)) означает,			что в качестве аргумента функции f(x)
служит само значение функции f(x), т.е.			f ( f ( x ) = ( 2 )	2x	. Очевидно, D(f(f)) = R.

Аналогично,	f ( g( x ) = 2log2 x = x	в силу основного логарифмического тож-
дества,	а		D(f(g))=(0;			+∞);
g( f ( x )) = log2 ( 2x ) = x log2 2 = x,		D( g( f )) = R;
g( g( x )) = log2 (log2 x ), D( g( g )) = ( 1; + ∞ ) , так как должно						выполняться
условие log2x > 0 x > 1. •

10. Найти функции f(g(x)) и g(f(x)), если
0, x ( −∞; 0 ]		0,
0, x ( −∞; 0 ]	, а
f ( x ) =	, а	g( x ) =	,
x, x ( 0; + ∞ )		−x2	,

x ( −∞; 0 ] x ( 0, + ∞ ).

•

Функции f и g – составные, причем D(f) = D(g) = R, E(f) = [0; +∞),

E(g) = (–∞; 0]. Так как D(f(g))=E(g), то f(g(x)) = 0, x (–∞; 0].

Аналогично, так как D(g(f))=E(f), то g(f(x)) = –x2,

x [0; +∞).

•

11. Найти f(f(f(x))), если f ( x ) =

1 − x2

•

Cоставим вначале сложную функцию f(f(x)), подставив в функцию f(x) вме-

сто аргумента x значение самой функции:

f ( f ( x )) =

1 − x2

1 − x

−

1 − 2x2

−

1 − x

Аналогично, теперь аргументом функции f(x) будет величина

;

1 − 2x2

f ( f ( f ( x ))) =

− 2 x2

1 − 2x

1 −

1 − 3x2

1 −

− 2x

1 −

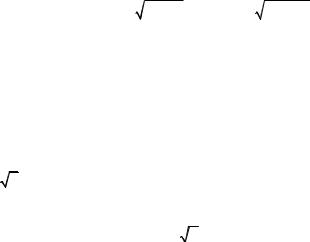
Заметим, что суперпозиция n функций			f ( x ) =			x	имеет вид	x	,
Заметим, что суперпозиция n функций			f ( x ) =			1 − x2	имеет вид	1 − nx2	,
где n N. •						1 − x2		1 − nx2
где n N. •
12. Определить функцию y = f(x), удовлетворяющую условию
	1			1
f x +		= x2 +				.
f x +		= x2 +		x	2	.
	x			x	2

	1		1	2
• Сделаем обозначение x +		= u , тогда x +		= u2 или
	x		x

x2 +	1	= u2 − 2 , \| u \| >	2 . Поэтому, заменяя x +	1	на u, а x2 +	1	на
	x2			x		x2

u2 − 2 , получим f(u) = u2 – 2. Если перейти к более привычному обозначению

аргумента буквой x, то получим, что f(x) = x2 – 2,			\| x \|		>		2 . •
13. Выяснить чётность определенных на R функций:						x
	2			1
а) cosx + sin2x; б) x3 + sinx; в) 2x		+ x ;	г)				− 3x .
					3

• а) f(–x) = cos(–x) + sin2(–x) = cosx + (–sinx)2 = cosx + sin2x = f(x).

Итак, f(x) – чётная функция.

б) f(–x) = (–x)3 + sin(–x) = – x3 – sinx = – (x3 + sinx) = – f(x) f(x) – нечёт-

ная функция.

в) f ( −x ) = 2( −x )2 − x = 2x2 − x ; f(x) – функция общего вида.

−x

г) f ( −x ) =

− 3

= 3

−

= −

− 3

= − f ( x ) f ( x ) –

нечётная функция.

•

14. Выяснить, какие из заданных функций являются периодическими и найти

их период Т:						б) f(x) = cos22x;
		а) f(x) = cos7x;				б) f(x) = cos22x;			в) f(x) = xsinx.
•		а) Имеем cos7x = cosu, где u = 7x. Известно, что cos(u + 2π) = cosu или
				2π			2π
cos7		x +			= cos7 x , т.е. f x +			=	f ( x ) . Итак, функция периодична и
cos7		x +			= cos7 x , т.е. f x +			=	f ( x ) . Итак, функция периодична и
				7			7
T =	2π		.
T =			.
		7

б) Преобразуем: cos2 2 x = 21 ( 1 + cos 4 x ) . Аналогично случаю а) легко пока-

зать, что cos4x периодическая функция с периодом 24π = π2 . Добавление к перио-

дической функции постоянной и умножение ее на постоянный множитель оставля-

ет ее периодической с тем же периодом. Итак, T = π2 .

в) f(x + T) = (x + T)sin(x +T) = (x + T)sinx ≠ f(x) – непериодическая функ-

ция. Очевидно, что произведение периодической функции на непериодическую есть непериодическая функция и в общем случае. •

15. Написать в явном виде функцию y, неявно заданную следующим уравнени-

ем:

а) 2xy = 5 ;	б) x + \|y\| = 2y.		1
• а) Решим уравнение 2xy = 5 относительно y:		xy = log2 5 y =	1	log2 5 .
• а) Решим уравнение 2xy = 5 относительно y:		xy = log2 5 y =	x	log2 5 .
			x

б) При решении модульного уравнения x + |y| = 2y, нужно рассмотреть вариан-

ты:

если y ≥ 0, то x + y = 2y y = x при x [0; +∞); если y < 0, то x – y = 2y y = 3x при x (–∞; 0).

Искомую функцию можно записать как составную:

x	при	x ( −∞;0 )
			•

y = 3
	при	x [0; + ∞ ).
x

16. Найти квадратный трехчлен f(x), если f(0) = 1, f(1) = 0 и f(2) = 5.

• Функция должна иметь вид: f(x) = ax2 + bx + c. Из условия задачи f(0) = c = 1, f(1) = a + b + c = 0, f(2) = 4a + 2b + c = 5.

Решим эту систему:

c = 1

a + b = −1

4a + 2b = 4 .

Отсюда c = 1, a = 3, b = – 4. Итак, искомая функция f(x) = 3x2 – 4x + 1. •

4.2 Задачи для самостоятельного решения

1. Написать выражение для площади S равнобочной трапеции с основаниями a = 2 и b = 1 как функции угла α при основании a.

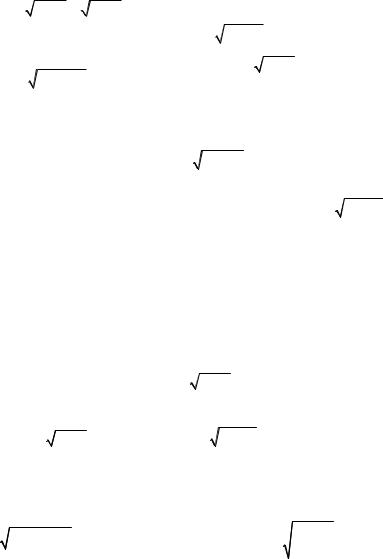
2. Напряжение в некоторой электрической цепи падает со временем по линейному закону. В начале опыта напряжение было 12 в, а по окончанию опыта, длившегося 8 сек, напряжение упало до 6,4 в. Выразить напряжение V как функцию времени t.

3. Найти естественные области определения функций:

а) f ( x ) =

x − 2 +

2 − x;

б) f(x) = lg cos2x;

в) f(x) = log2 log2x;

г)

f ( x ) = 1− | x | ;

д)

f ( x ) =

;

е)

f ( x ) = arcsin

1 − x .

x2 − 3x

4. Найти множество Y, на которое данная функция отображает множество Х:

а)

y = x2,

X = [–1; 2];

б)

y = |x|,

X = {x: x [–5; –3] U[1; 3]};

в)

y =

, X = (0; 0,5);

г)

y =

x − x2 ,

X = (0; 1).

2 x −

5. Найти

f ( 0 ),

−

f ( −x ), f

если f ( x ) =

1 + x

f ( x )

f(x) = arccos(lgx).

6. Найти

, f ( 1 ),

f ( 10 ) для

7. Найти для перечисленных ниже функций обратные и указать их области определения:

				x				1	− x
а)	f(x) = lg2x ;	б)	f ( x ) = 2	2	;	в)	f ( x ) =			;
								1
									+ x
г)	f(x) = 2sin3x;	д)	f ( x ) = 4 arcsin 1 − x .
8. Выразить y как функцию от х и указать её область определения, если
а)	y = z2 , z = 3 u + 1, u = 10 x ;					б) y =	1 − u2 , u = cosv, v = 1 + x ;
в) y = u3, u = arctg v, v = lg w,						w = x – 1.

9. Суперпозицию каких основных элементарных функций представляют заданные сложные функции:

а) y =	sin(lg2	x ) ; б) y = 10arcsin	2	( x	2	) ; в)	y = tg 3	1	.
								1 + 2x

10. Составить f(f(x)), f(g(x)), g(f(x)),				g(g(x)) и указать их области опреде-

ления, если

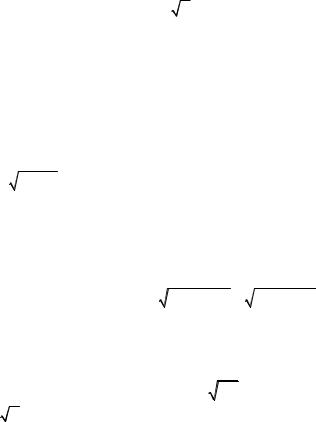
а)	f ( x ) = 2x ,				g(x) = x2 ;	б)	f ( x ) = 3 x , g( x ) = lg x .
11. Даны функции f(x) = x3 – x,						g(x) = sin2x. Найти:
			π
а)	f g			;	б) g(f(1));		в) g(f(2));

			12
г) f(g(x));					д) f(f(x));	е) f(f(f(1))).
12. Найти f(x + 1), если f(x – 1) = х2.
13. Определить функцию y = f(x), если
		1			1 + x2 , x > 0 ;		б) f(x + 1) = x2 – 3x + 2.
а)	f		= x +

		x

14. Определить, какие из данных функций являются чётными, а какие нечётными:

1)	f(x) = 3x – x3;			2) f ( x ) = lg	1	+ x	;
					1	− x
		1
3)	f ( x ) =		( 2x + 2−x ) ;	4) f ( x ) = 1 + x + x2 − 1 − x + x2 .
		2

В качестве ответа перечислить номера нечётных функций.

15. Определить, какие из перечисленных ниже функций являются периодическими, и для периодических функций найти их период T:

а) f(x) = 10sin3x;	б)	f(x) = sin2x; в) f ( x ) = tgx ;
г) f ( x ) = sin x ;	д)	f(x) = sinx + cos2x.

16. Найти линейную функцию f(x), если f(–1) = 2, f(2) = –3.

17. Записать в явном виде функции y, неявно заданные уравнениями:

а) lgx + lg(y + 1) = 4;	б) x3 + y3 = 1;
в) 2x+ y (x2 – 2) = x3 + 7;	г) (1 + x)cosy – x2 = 0 .

Глава 3. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИИ

Понятия предела и непрерывности функции – фундаментальные понятия математического анализа. Операция предельного перехода является одной из основных математических операций. Изучив данную главу, читатель подготовит себя к восприятию понятий производной и интеграла.

Ограничимся изучением предела действительных функций действительного аргумента, а также предела числовой последовательности, т.е. предела функций натурального аргумента.

При рассмотрении вопросов, связанных с пределом функции, будем использовать понятие проколотой окрестности U°(a) = U(a)\{a} точки a R числовой

прямой, т.е. окрестности U(a) за исключением самой точки a.
Аналогично для проколотой δ – окрестности
Uδo ( a ) =Uδ ( a )\{a} ={ x R : 0 < x − a <δ} .	(1)

Проколотые окрестности бесконечно удалённых точек +∞ , –∞ и их объединения ∞ будем считать совпадающими с окрестностями этих точек, т.е. при М ≥ 0

U o( +∞ ) =U( +∞ ) ={x R : x > M} = ( M , + ∞ ), U o( −∞ ) =U( −∞ ) ={x R : x < −M} = ( −∞, − M ), U o( ∞ ) =U( ∞ ) ={x R : | x |> M} = R \ [ −M ,M ] .

1. ПОНЯТИЕ ПРЕДЕЛА ФУНКЦИИ

Рассмотрим функцию f(x), определённую, по крайней мере, в некоторой проколотой окрестности U°(a) точки а числовой прямой R .

Определение 1. Число b называют пределом функции f(x) в точке a (или при х

стремящемся к а) и обозначают b = lim f ( x ) , если, какова бы ни была окрест-

x→a

ность U(b) точки b, найдётся такая окрестность U°(a) точки a, что все значения функции f(x) будут заключены в U(b) при условии, что значения аргумента x взяты из U°(a), т.е.

b = lim f ( x ) : U( b ) U o( a ) : ( x U o( a ) f ( x ) U( b )) . (2)

x→a

При обозначении предела иногда пишут f(x) → b при x → а и читают так: « f(х) стремится к b при x стремящемся к а ».

Замечание. Это достаточно общее определение предела функции и в нём точки а и b числовой прямой не обязательно конечны. Важно лишь правильно выбрать окрестности, когда эти точки конечны и когда они таковыми не являются. Рассмотрим подробно различные случаи.

1.1 Конечный предел функции в конечной точке

Для конечных точек а и b при условии, что область определения рассматриваемой функции включает некоторую проколотую окрестность точки а, вместо определения 1 с учетом (1) можно сформулировать следующее определение.

Определение 2. Число b называют пределом функции f(x) в точке а (или при x стремящемся к а), если для любого сколь угодно малого положительного числа ε найдется другое положительное число δ, такое, что для всех точек проколотой δ

– окрестности точки а значения функции f(x) принадлежат ε – окрестности точки b, т.е.

b = lim f ( x ) : ε > 0 δ( ε ) > 0 : ( 0 <| x −a |<δ | f ( x ) −b |< ε ) . (3)

x→a

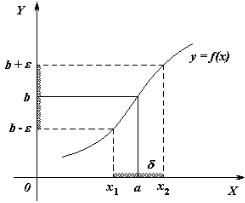
Запись δ(ε) в (3) подчеркивает, что значение δ зависит от выбора ε. Определение 2 имеет простое геометрическое толкование (рисунок 1).

Для нахождения δ при заданном ε по графику функции следует найти ближайшие к а точки x1 и x2 из условий: f(x1) = b – ε , f(x2) = b + ε и положить

δ равным меньшему из расстояний от точки а до найденных точек. Как правило, при уменьшении числа ε будет

уменьшаться и число δ.

Замечания.

1) Согласно определениям 1 и 2 точка а может и не принадлежать области определения функции, а если и принадлежит, то значение f(а) не учитывается.

Рисунок 1

2)Для получения зависимости δ от ε стараются оценить |f(x) – b| через |x – a|

инайти ограничения на последнюю величину.

Пример 1. Покажем, что если f(x) = C = const, то lim f ( x ) = C .

x→a

• Действительно, x f(x) – C = C – C = 0 < ε, если ε – любое положительное число. Поэтому в качестве δ можно взять любое положительное число. •

Пример 2. Покажем, что lim x = a .

x→a

• Возьмём произвольное число ε > 0 и предположим, что |f(x) – a| = |x – a| < ε. Это неравенство будет справедливо x Uδo ( a ), если взять δ = ε. •

<<< < Предыдущая 1 2 3 4 56 / 236 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.02.20151.73 Mб316matem-up1.pdf
#
14.02.201554.78 Кб17Matematika-i-statistika-12-RiSO-B.doc
#
14.02.2015543.23 Кб30matematika_ekzamen - .doc
#
14.02.20152.69 Mб320matematika_metod_posobie.docx
#
14.02.20151.69 Mб232Matematika_ryad.doc
#
14.02.20152.17 Mб54Matematika_Zaytsev_ch2.pdf
#
14.02.20158.95 Mб92matematike_fepo_s_otvetami.doc
#
24.08.20193.22 Mб24materialoved.doc
#
14.02.2015899.5 Кб40mcad_pract.pdf
#
14.02.2015203.78 Кб25mech.doc
#
15.11.2019323.76 Кб7Meeting clients.docx