Matematika_Zaytsev_ch2
.pdf
В частности, если α = 0, |
β = |
π |
, (т. е. s = |
|
), то |
∂ z |
= |
∂ z |
; если же α = |
π |
, |
||||||
i |
|||||||||||||||||
2 |
∂ s |
∂ x |
2 |
||||||||||||||
|
|
|
∂ z |
|
|
∂ z |
|
|
|
|
|
|
|||||
β = 0 (т.е. s = |
|
), то |
= |
. Таким образом, частные производные по x и y |
|||||||||||||
j |
|||||||||||||||||
∂ s |
∂ y |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
являются частным случаем производной по направлению.
Формула (16) говорит о том, что для дифференцируемой функции двух переменных знание частных производных (т. е. производных по двум взаимно перпендикулярным направлениям) позволяет написать выражение производной по любому направлению.
Замечания.
1.Если направление задаётся вектором a ={ ax ,ay } , то cosα = aarx , cos β = aary .
2. При замене направления на противоположное производная по направлению меняет знак.
Пример 16. Вычислить производную функции z = x3y − 5xy2 + 1 в точке
M(1; 1) по направлению вектора MN , где N - точка с координатами (0; 2).
• Имеем |
MN |
= { 0 − 1; 2 − 1 } = { −1; 1 } , |
MN |
|
= ( −1 )2 +( 1 )2 |
= |
2 . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
1 |
|
|
|
|
|
|
|
|
данном направлении s = |
|
MN |
; |
|||||||||
Единичный |
вектор |
в |
|
|
|
|
= |
|
|
, т. е. |
|||||||||
|
|
|
|
2 |
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
MN |
|
|
|
|
|
||
cosα = − |
1 |
, |
cos β = |
1 |
. Найдём частные производные функции z в точке M: |
||||||||||||||
|
2 |
||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
z′x ( x, y ) = 3x2 y − 5 y2 z′x ( M ) = −2, z′y ( x, y ) = x3 − 10 xy z′x ( M ) = −9.
|
∂ z |
|
|
|
|
1 |
|
|
1 |
|
7 |
|
|
|
|
|
|
|
|
|
|||||||
По формуле (16) получим |
∂ s |
|
|
= −2 |
− |
|
|
− 9 |
|
= − |
|
. |
• |
|
|
2 |
2 |
2 |
|||||||||
|
|
M |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
При изучении поведения функции в данной точке бывает важно найти направление, вдоль которого скорость изменения функции наибольшая в этой точке. Эта задача решается очень просто с помощью вектора, называемого градиентом.
Вектор с координатами z′x , z′y в точке M(x, y) называется градиентом функции
z = f(x, y) в этой точке и обозначается grad f(M) или grad z. |
|
||||||
Итак, по определению, |
|
||||||
grad z ={z′x , z′y } = z′x |
|
+ z′y |
|
. |
(17) |
||
i |
j |
||||||
Рассмотрим основные свойства градиента. |
|
||||||
1. Проекция градиента функции z = f(x, y) на направление s |
равна производной |
||||||
функции по этому направлению, т. е. ПРs grad z = |
∂ z |
. |
|
||||
|
|
||||||
|
|
|
∂ s |
|
|||
187 |
|
|
|
|
|
|
|
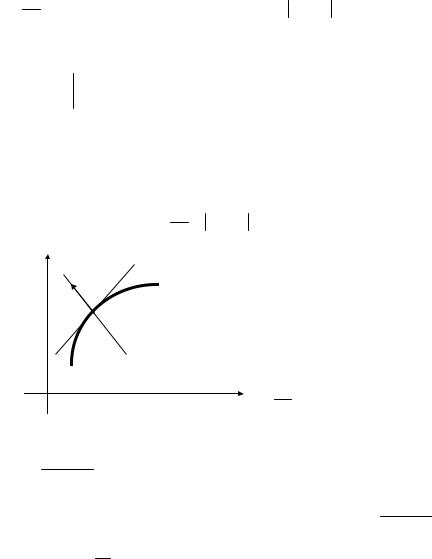
Действительно, записывая ∂ z |
с помощью скалярного произведения, имеем для |
||||||
|
∂ s |
|
|
|
|
|
|
любого направления s : |
|
|
|
|
|
|
|
∂ z = {z′x , z′y } {cosα , cos β |
} = grad z |
s = grad z cosϕ = ПРs grad z , |
|||||
∂ s |
|
|
|
|
|
|
|
где ϕ - угол между векторами s и grad z . |
|
|
|
|
|
||
2. Градиент функции z в точке M указывает направление, вдоль которого про- |
|||||||
изводная ∂ z |
максимальна (направление наибольшей скорости изменения функ- |
||||||
∂ s |
M |
|
|
|
|
|
|
ции в точке М). При этом модуль градиента равен этой наибольшей скорости |
|||||||
изменения функции в данной точке. |
|
∂ z имеет наибольшую вели- |
|||||
Действительно, из первого свойства следует, что |
|||||||
|
|
|
|
∂ s |
|
|
|
чину при cosϕ = 1 (при ϕ = 0), т. е. когда направление вектора s |
совпадает с на- |
||||||
правлением grad z, при этом ∂ z |
= grad z . |
|
|
|
|
|
|
|
∂ s |
|
|
|
|
|
|
Y |
|
|
3. Градиент функции z = f(x, y) |
||||
grad z(M0) |
|
в точке M0(x0, y0) направлен по |
|||||
|
f(x, y)=c |
нормали к линии уровня этой функ- |
|||||
|
M0 |
|
ции, проходящей |
через точку M0 |
|||
|
|
(рисунок 6). |
|
|
|
||
|
|
|
|
|
|
||
T |
|
|
Действительно, |
угловой |
коэф- |
||
N |
|
фициент k1 касательной T к линии |
|||||
|
|
||||||
|
|
|
уровня f(x, y)=c равен производной |
||||
|
|
|
dy |
|
|
|
|
0 |
Рисунок 6 |
X |
dx в точке M0 (здесь c = f(x0, y0)). |
||||
|
|
Согласно правилу |
дифференциро- |
||||
k1 = − fx′( M0 ) . Угловой коэффициент k2 |
вания |
неявной |
функции |
имеем |
|||
прямой N, параллельной градиенту, |
|||||||
f y′( M0 ) |
|
|
|
|
|
|
|
равен отношению второй координаты вектора к первой, т. е. k2 = |
|
f y′( M0 ) |
. Таким |
||||
|
|
|
|
|
|
fx′( M0 ) |
|
образом, k2 |
= − 1 (условие перпендикулярности двух прямых). Значит, градиент |
||||||
|
k1 |
|
|
|
|
|
|
имеет направление, перпендикулярное к касательной, т. е. градиент направлен по |
|||||||
нормали к линии уровня. |
|
|
|
|
|
|
|
188
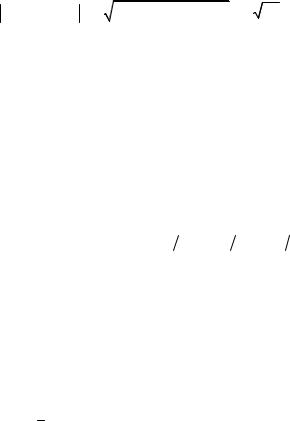
Аналогично определяется производная функции трёх переменных u = f(x, y, z)
по направлению вектора s = {cosα, cos β , cosγ } , выводится формула |
|
||
|
∂ u |
= u′x cosα + u′y cos β + uz′ cosγ , |
(16/) |
|
|
||
|
∂ s |
|
|
вводится понятие градиента |
|
||
|
|
grad u ={u′x ,u′y ,uz′} |
(17/) |
и исследуются его свойства.
Пример 17. Найти grad u и grad u в точке M(3; 2; 1), если u = 4− x2− y2+z2.
• Вычислим частные производные и их значения в точке M:
u′x = −2x, u′y = −2 y, uz′ = 2z u′x ( M ) = −6 , u′y ( M ) = −4, uz′( M ) = 2 . Поэтому, grad u(M) = {− 6; − 4; 2} = 2{− 3; − 2; 1},
grad u( M ) = 2 ( −3 )2 + ( −2 )2 + 12 = 2 14 . •
Понятия производной по направлению и градиента функции играют важную роль во многих приложениях.
3.3 Касательная плоскость и нормаль к поверхности
Рассмотрим вначале пространственную линию L, координаты текущей точки M(x, y, z) которой можно задать как функции от некоторого параметра t:
x = x(t), y = y(t), z = z(t).
Возьмём на этой линии какую-либо точку M0(x0, y0, z0), определяемую значением параметра t = t0, т. е. x0 = x(t0), y0 = y(t0), z0 = z(t0). Придадим t0 приращение
∆t, тогда значению параметра t0 + ∆t будет соответствовать другая точка M1(x0+∆x, y0+∆y, z0+∆z) на линии L. Уравнения секущей M0M1 будут иметь вид:
x − x0 |
= |
y − y0 |
= |
z − z0 |
или |
x − x0 |
= |
y − y0 |
= |
z − z0 |
, |
|
∆x |
∆y |
∆z |
∆x ∆t |
∆y ∆t |
∆z ∆t |
|||||||
|
|
|
|
|
|
где x, y, z - координаты текущей точки секущей.
Если эти уравнения в пределе при ∆t→ 0 сохраняют определённый смысл, то этим будет установлено существование предельного положения секущей, т. е. касательной. Итак, уравнения
x − x0 |
|
= |
y − y0 |
|
= |
z − z0 |
|
(18) |
|
x′( t0 ) |
y′( t0 ) |
z′( t0 ) |
|||||||
|
|
|
|||||||
представляют прямую, являющуюся касательной к пространственной линии
L: x = x(t), y = y(t), z = z(t) в точке M0(x0, y0, z0) при условии, что x’(t0), y’(t0), z’(t0) одновременно не обращаются в нуль.
Отметим, что вектор τ ( M0 ) ={x′( t0 ), y′( t0 ),z′( t0 )} параллелен касательной,
его называют касательным вектором к линии L в точке M0 (при значении параметра t0).
189
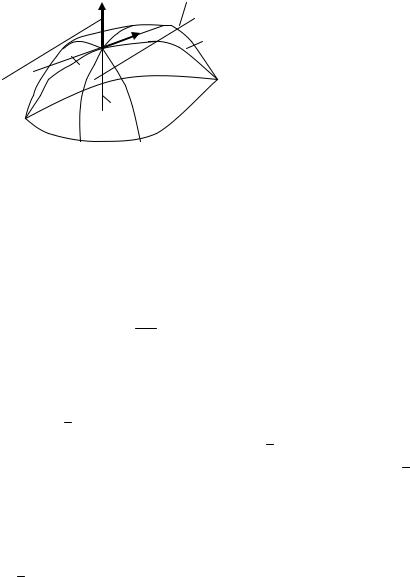
|
|
r |
P |
Рассмотрим теперь поверхность Σ, зада- |
|
|
|
n |
|
|
|
|
|
|
|
|
ваемую уравнением z = f(x, y) (явное зада- |
|
|
|
|
|
|
|
|
τ |
|
Σ |
ние поверхности) или в общем случае урав- |
M0 |
|
нением F(x, y, z) = 0. |
|||
L |
|
|
Пусть M0(x0, y0, z0) - какая-либо точка |
||
|
|
|
|
|
поверхности Σ (рисунок 7). Проведём через |
|
|
|
|
|
|
Nточку M0 по поверхности Σ произвольную линию L и в названной точке построим к
этой линии касательную. Таких линий (и Рисунок 7 касательных к ним) существует бесконечно
много.
Если все такие касательные лежат в одной плоскости P, то эту плоскость называют касательной плоскостью к поверхности Σ в точке M0 (точка M0 - точка касания).
Так как линия L Σ, то F(x(t), y(t), z(t)) ≡ 0 (*), где x(t), y(t), z(t) - парамет-
рические уравнения линии L. В частности, F(M0) = F(x(t0), y(t0), z(t0)) = 0, пото-
му что M0 L, M0 Σ.
Применяя правило дифференцирования сложной функции F, зависящей через промежуточные переменные x, y, z от независимой переменной t и учитывая тождество (*), получим: dFdt = Fx′ x′ + Fy′ y′ + Fz′ z′ = 0 . При t = t0 имеем
Fx′( M0 ) x′( t0 ) + Fy′( M0 ) y′( t0 ) + Fz′( M0 ) z′( t0 ) = 0 .
Полученное равенство можно записать в виде равенства нулю скалярного произведения вектора grad F( M0 ) ={Fx′( M0 ),Fy′( M0 ),Fz′( M0 )} и касательного
вектора τ ( M0 ) ={x′( t0 ), y′( t0 ),z′( t0 )} к линии L в точке M0: grad F ( M0 ) τ ( M0 ) = 0 .
Вектор grad F(M0) есть постоянный вектор в точке M0, а вектор τ
сательный вектор к линии L в точке M0 и поэтому зависит от выбора L, т. е. является переменным вектором.
Так как скалярное произведение этих векторов равно нулю, то эти векторы пер-
пендикулярны |
при любом выборе L, |
а |
это |
означает, что |
вектор |
||
n( M0 |
) = grad |
F( M0 ) перпендикулярен |
ко |
всем |
касательным |
векторам |
|
τ |
( M0 |
) в точке M0, т. е. перпендикулярен касательной плоскости P к поверхности |
|||||
Σ в точке M0 (вектор n( M0 ) - вектор нормали).
Итак, касательная плоскость P проходит через точку M0(x0, y0, z0) и перпендикулярна вектору n(r M0 ) ={Fx′( M0 ), Fy′( M0 ), Fz′( M0 )}, поэтому её уравнение, как следует из аналитической геометрии, имеет вид:
190
P : Fx′( M0 )( x − x0 ) + Fy′( M0 )( y − y0 ) + Fz′( M0 )( z − z0 ) = 0 . (19)
Назовём нормалью к поверхности Σ в точке M0 прямую N, проходящую через точку M0 и перпендикулярную к касательной плоскости P в этой точке.
Так как нормаль проходит через точку M0(x0, y0, z0), а вектор n( M0 ) − её направляющий вектор, то её канонические уравнения имеют вид:
|
x − x |
0 |
|
|
y − y |
|
|
z − z |
0 |
|
|
|
||
N : |
|
|
|
= |
|
0 |
|
= |
|
|
. |
(20) |
||
′ |
( M0 |
) |
′ |
( M0 |
) |
′ |
|
|||||||
|
Fx |
|
Fy |
|
Fz ( M0 ) |
|
|
|||||||
Замечания.
1. Если поверхность Σ задана явным уравнением z = f(x, y), то уравнение каса-
тельной плоскости в точке M0(x0, y0, z0) получает вид: |
|
z − z0 = fx′( M0 )( x − x0 ) + f y′( M0 )( y − y0 ) . |
(19/) |
Действительно, записав уравнение z = f(x, y) в виде f(x, y) – z = 0, имеем
F( x, y,z ) = f ( x, y ) − z; Fx′ = fx′, Fy′ = fy′, Fz′= −1 и, используя уравнение (19),
получим уравнение (19/).
Уравнения нормали (20) примут вид:
x − x0 |
|
= |
y − y0 |
|
= |
z − z0 |
|
/ |
|
|
|
|
|
. |
(20 ) |
||
fx′( M0 |
) |
f y′( M0 |
) |
−1 |
2. Градиент функции u = f(x, y, z) в точке M0(x0, y0, z0) направлен по нормали к поверхности уровня этой функции, проходящей через точку M0.
Действительно, поверхность уровня, на которой лежит точка M0, имеет уравне-
ние f(x, y, z) = c, где c = f(M0) или |
f(x, y, z) − c = 0. Как было выше получено, |
|||||
вектор n( M |
′ |
|
′ |
′ |
} |
= grad f ( M0 ) есть вектор |
0 ) ={( f − c )x |
, ( f − c )y |
, ( f − c )z |
||||
|
|
|
|
|
|
M0 |
нормали к поверхности в точке M0, что и доказывает утверждение.
Пример 18. Найти уравнение касательной плоскости и нормали к эллиптическому параболоиду z = 2x2+y2 в точке M0(1; −1; 3).
• Так как поверхность задана явно относительно z, то воспользуемся формула-
ми (19/) |
и (20/). Здесь x0 |
= 1, y0= − 1, z0 = 3. Имеем fx′( M0 |
) = 4x |
= 4 , |
|||||||
|
|
|
|
|
|
|
|
|
|
|
M0 |
fy′( M0 |
) = 2 y |
= −2 . Итак, уравнение касательной плоскости P: |
|
|
|||||||
|
|
M0 |
|
|
|
|
|
|
|
|
|
|
|
z − 3 = 4(x − 1) + (−2)(y + 1) |
или 4x − 2y − z − 3 = 0. |
||||||||
Уравнение нормали N: |
|
x − 1 |
= |
y + 1 |
= |
z − 3 |
. • |
|
|
||
4 |
−2 |
−1 |
|
|
|||||||
|
|
|
|
|
|
|
|
||||
191
3.4 Экстремум функции нескольких переменных
Понятие экстремума функции нескольких переменных во многом аналогично понятию экстремума функции одной переменной, особенно если при этом использовать термины «функция точки», «окрестность точки». В основном рассматривается случай, когда точка M – точка на плоскости OXY, т. е. M(x, y), или в пространстве OXYZ, тогда M(x, y, z).
Дадим определение. Говорят, что функция u = f(M) в точке M0 имеет локальный максимум (минимум), если в некоторой окрестности U( M0 ) этой точки зна-
чение f(M0) не меньше (не больше) значения функции в любой другой точке этой окрестности, т. е.
f(M0) ≥ f(M) ( f(M0) ≤ f(M) ) M U( M0 ) .
Локальный максимум и минимум объединяются общим названием экстремум. Точку M0 называют в этом случае точкой экстремума.
В своей области определения функция может совсем не иметь экстремума, а может иметь несколько максимумов, несколько минимумов. При этом максимумы могут оказаться меньше некоторых из её минимумов. Не следует путать максимумы и минимумы функции с её наибольшим и наименьшим значениями.
Из определения следует, что если функция u = f(M) имеет экстремум в точке M0, то приращение ∆u(M0) = f(M) – f(M0) этой функции в точке M0 удовлетворяет в окрестности U( M0 ) одному из условий: ∆u(M0) ≤ 0 (если M0 – точка мак-
симума) или ∆u(M0) ≥ 0 (если M0 – точка минимума). Обратное утверждение тоже верно: если в некоторой окрестности точки M0 выполняется одно из этих неравенств, то функция имеет экстремум в этой точке.
Выясним необходимые и достаточные условия того, чтобы точка M0 являлась точкой экстремума функции u = f(M).
Теорема 8 (необходимое условие экстремума).
Пусть функция u = f(M) имеет экстремум в точке M0 и дифференцируема в этой точке. Тогда все частные производные первого порядка в точке M0 обращаются в нуль.
Доказательство проведем для случая максимума в точке M0 и ограничимся случаем функции двух переменных u = f(M) = f(x, y). Тогда, по определению, существует окрестность точки M0(x0, y0), для всех точек M(x, y) которой выполняется условие f(x, y) ≤ f(x0, y0). В частности, f(x, y0) ≤ f(x0, y0). Это значит, что функция одной переменной f(x, y0), дифференцируемая при x = x0, имеет макси-
мум при x = x0 и, следовательно, выполняется необходимое условие экстремума функции одной переменной:
df ( x , y0 ) |
|
= 0 |
∂f |
|
= |
∂f |
|
|
= 0 . |
|
|
|
|||||||||
dx |
|
x=x0 |
∂x |
xy==xy0 |
∂x |
|
M0 |
|||
|
|
|
|
|
|
|||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
192 |
|
|
|
|
|
|
|

Аналогично, рассматривая функцию f(x0, y), получим |
∂f |
|
=0. Случай мини- |
|
|||
|
∂y |
|
M0 |
мума функции в точке M0 аналогичен. |
|
|
|
Замечания.
1. Необходимому условию экстремума в точке M0 дифференцируемой функции u = f(M) можно придать и другие, эквивалентные, формулировки:
du(M0) = 0 grad u(M0) = 0 |
∂u |
|
= 0 s . |
|
|||
|
∂s |
|
M0 |
Рекомендуется читателю самостоятельно убедиться в эквивалентности приведенных формулировок необходимого условия экстремума.
2. Необходимое условие экстремума не является достаточным. Например, частные производные функции u = x2 – y2 равны нулю в точке O(0; 0), поэтому необходимое условие экстремума в этой точке выполнено. Однако данная функция не имеет экстремума в указанной точке, так как в любой окрестности точки O найдутся как положительные (например, при y = 0), так и отрицательные значения u (например, при x = 0), т. е. значения большие и меньшие, чем нулевое значение u в точке O.
Итак, точками экстремума дифференцируемой функции могут быть только те точки, в которых все частные производные первого порядка обращаются в нуль (критические точки функции).
Ясно, что если дифференцируемая функция не имеет критических точек, то она не имеет и точек экстремума.
Установим теперь достаточное условие экстремума (ограничимся только случаем функции двух переменных).
Теорема 9 (достаточное условие экстремума).
Пусть в критической точке M0(x0, y0) и некоторой её окрестности функция z = f(x, y) имеет непрерывные частные производные второго порядка. Тогда точка M0 является точкой экстремума данной функции, если d2f(M0) знакопостоянен
для любых ∆x и ∆y и обращается в нуль только при ∆x = ∆y = 0. При этом точка M0 – точка максимума, если d2f(M0) < 0; M0 – точка минимума, если d2f(M0) > 0.
Доказательство основано на применении формулы Тейлора к данной функции
в точке M0 при n = 2: |
1 |
|
f ( M0 ) + o( |
|
|
|
2 ) . |
|
∆ f ( M0 ) = df ( M0 ) + |
d 2 |
|
M0 M |
|
||||
|
|
|||||||
2 |
||||||||
|
|
|
|
|
|
|
Так как точка M0 – критическая точка, то df(M0) = 0. Итак, приращение функции в точке M0 представлено в виде суммы двух б. м. при M→ M0 (или ∆x→ 0,
∆y→ 0): первое слагаемое 21 d 2 f ( M0 ) имеет второй порядок малости, а второе
193

слагаемое o( M0 M 2 ) – больший порядок, чем два, по сравнению с величиной
M0 M . Поэтому в достаточно малой окрестности U( M0 ) точки M0 (при доста-
точно малых ∆x и ∆y) если дифференциал второго порядка d2f(M0) знакопостоянен, то и приращение ∆f(M0) будет одного знака, а это означает, что точка M0 – точка экстремума для функции f(M). При этом если Μ U( M0 ) d2f(M0) > 0,
то ∆f(M0) > 0 Μ U( M0 ) , поэтому M0 – точка минимума; если Μ U( M0 )
d2f(M0) < 0, то ∆f(M0) < 0 Μ U( M0 ) , поэтому M0 – точка максимума. |
|
|
|
||||||||||||||
|
|
Пример 19. |
Исследовать на экстремум функцию f(x, y) = x2 + y2 – 6x. |
|
|
|
|||||||||||
|
|
• Имеем fx′ = 2x − 6 , |
f y′ = 2 y . Определим критические точки функции, |
для |
|||||||||||||
этого решим систему: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
f |
′ = 2 x − 6 = 0 |
|
x |
= 3 |
|
|
|
|
|
|
|
||
|
|
|
|
|
x |
|
|
|
, |
M0(3; 0) – критическая точка. |
|
|
|||||
|
|
|
|
|
|
|
|
|
= 0 |
|
|
||||||
|
|
|
|
f y′ = 2 y = 0 |
|
|
y |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдем второй дифференциал функции f в точке M0: |
|
|
|
|
|
||||||||||
|
2 |
|
′′ |
|
2 |
′′ |
|
|
|
|
|
′′ |
2 |
2 |
2 |
|
|
d |
|
f ( M0 |
) = fxx |
( M0 )( ∆x ) |
+2 fxy |
( M0 )∆x∆y + fyy ( M0 )(∆y ) |
=2(∆x ) +2( |
∆y ) |
|
= |
|||||||
|
|
|
= 2[(∆x)2 + (∆y)2] > 0 |
∆x, ∆y, кроме случая ∆x = ∆y = 0. |
|
|
|
||||||||||
|
|
Итак, критическая точка M(3; 0) является точкой минимума, а значение функ- |
|||||||||||||||
ции в этой точке f(M0) = f(3; 0) = –9. |
• |
|
|
|
|
|
|
|
|||||||||
Рассмотрим удобный для решения задач признак наличия или отсутствия экстремума в критической точке, являющийся признаком знакопостоянства и знакопеременности второго дифференциала функции.
Теорема 10 (признак Сильвестра).
Пусть в критической точке M0(x0, y0) и некоторой её окрестности функция z = f(x, y) имеет непрерывные частные производные второго порядка. Положим
D = |
A B |
= A C − B |
2 |
′′ |
( M0 |
), |
′′ |
( M0 |
′′ |
( M0 |
) . |
|
|
||||||||||
B C |
|
, где A = fxx |
B = fxy |
), C = f yy |
|||||||
|
|
|
|
|
|
|
|
|
|
|
Тогда:
1)если D > 0, то в точке M0 функция f(M) имеем экстремум (максимум, если A < 0, минимум, если A > 0);
2)если D < 0, то в точке M0 функция f(M) не имеет экстремума.
Доказательство. Запишем второй дифференциал функции в точке M0:
d2f(M0) = A(∆x)2 + 2B∆x∆y + C(∆y)2. (*)
Здесь хотя бы одно из приращений ∆x и ∆y не равно нулю (пусть ∆y ≠ 0). Тогда выражение (*) можно представить в виде:
2 |
|
2 |
|
2 |
|
|
∆x |
|
d |
f(M0) = (∆y) |
|
(Ak |
|
+ 2Bk + C), где |
k = |
|
. |
|
|
∆y |
||||||
|
|
|
|
|
194 |
|
|
|

Знак второго дифференциала d2f(M0) равен знаку выражения Ak2 + 2Bk + C. Условие знакопостоянства квадратного трехчлена Ak2 + 2Bk + C: дискриминант B2– AC < 0 D > 0. А это и есть достаточное условие экстремума функции в точке M0 (на основании теоремы 9).
При этом квадратный трехчлен будет иметь только отрицательные значения (а, значит, и второй дифференциал), если A < 0. По теореме 9 точка M0 будет точкой максимума. Случай A > 0 аналогичен.
При D < 0 нарушается условие знакопостоянства второго дифференциала в точке M0 и экстремума в этой точке не будет. Принимаем этот факт без доказательства.
Замечание. Если D = 0, то функция f(x, y) в критической точке M0 может иметь экстремум, но может и не иметь его. Это подтверждается, например, рассмотрением функций f(x, y) = x4 + y4 и f(x, y) = x4 – y4 в окрестности точки O(0;0). Советуем читателю самостоятельно убедиться, что для первой функции точка O – точка минимума, а вторая функция в точке O не имеет экстремума, хотя в обоих случаях D = 0.
Пример 20. Исследовать на экстремум функцию z = − |
|
2 |
x3 |
+ 2xy − y2 − 1 . |
||||||
3 |
||||||||||
|
|
|
|
|
|
|
|
|||
• Находим частные производные z′x = −2 x2 + 2 y, z′y |
|
= 2x − 2 y . Приравнивая |
||||||||
их нулю, составим систему и решим ее: |
|
|
|
|
|
|
|
|||
|
−2x2 + 2 y = 0 |
y = x2 |
x = 0 |
|
|
x = 1 |
. |
|||
|
2 x − 2 y = 0 |
|
|
и |
= 1 |
|||||
|
y = x |
y = 0 |
|
|
y |
|
||||
Получили две критические точки M1(0; 0) и M2(1; 1). Вычислим частные про-
′′ |
= −4 x, |
′′ |
= 2, |
′′ |
= −2 . Так как |
изводные второго порядка: zxx |
zxy |
zyy |
A1 = z′′xx ( M1 ) =0, B1 = z′′xy ( M1 ) =2, C1 = z′′yy ( M1 ) =−2, D1 = A1C1 −B12 =−4 <0 ,
то в точке M1 экстремума нет. В точке M2:
A2 = z′′xx ( M2 ) = −4, B2 = B1 = 2, C2 = C1 = −2, D2 = A2C2 − B22 = 4 > 0 .
Точка M2 – точка максимума, так как D2 > 0 и A2 < 0. Значение максимума f ( M2 ) = − 23 . •
3.5 Наименьшее и наибольшее значения функции
Пусть на плоскости OXY дана замкнутая область G с границей L. Пусть внутри области G и на границе L задана дифференцируемая функция z = f(x, y) и требуется найти наименьшее m и наибольшее M значение функции z в этой замкнутой области G.
Существование таких значений следует из непрерывности функции z в замкнутой области.
195