Matematika_Zaytsev_ch2

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Алтайский государственный технический университет им. И.И.Ползунова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

10sin2 t − 1

10sin2 t − 1

ln( 1 − 2 sin

.pdf

Скачиваний:

Добавлен:

14.02.2015

Размер:

2.17 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 2310 11 12 13 14 15 16 17 18 19 20 21 22 23 > Следующая >>>

•

sin π t ~

= lim sin 2 t

π t

t→0

Найти lim

tgx − sin x

x→0

sin x −

tgx − sin x

lim

= lim

cos x

x→0

	π
= lim	2 t	=	π	. •
= lim	t	=	2	. •
t→0	t		2

sin x	sin x( 1 − cos x )
= lim		=
	x3 cos x
x→0


	sin x 2 sin			2	x		x	~ x		2
= lim					2	= sin x ~ x , 2 sin2					=
	x	3	cos x
x→0						x→0	2 x→0		2

= lim

. Итак, tgx − sin x

. •

cos x

x→0

6. Найти lim

x (tgx2 + 2 x)

x→0

x sin2 x − arctgx

• lim

x (tgx2 + 2 x)

= lim

tgx2

+ 2 x

arctgx

x sin2 x

− arctgx

x→0

sin

x −

lim arctgx		= 1	= 0 .
x→0	x

•

7. Найти

• Так как

x − 3 2 x+1 lim . x→∞ x + 2

lim	x − 3	= 1 , а	lim ( 2 x + 1 ) = ∞ , то имеем предел, связанный с

x→∞ x + 2			x→∞

раскрытием неопределенности вида ( 1∞ ). Чтобы воспользоваться вторым замечательным пределом, сделаем преобразования:

2 x+1

x+2 −5

( 2 x+1 )

x − 3

−5

x+2

lim

− 1

= lim

x + 2

x→∞ x + 2

x→∞

−5

x+2

lim

−10 x−5

−5

lim

= e = ex →∞

x+2

= e−10

. •

x +

x→∞

8. Найти lim (cos x )x .

x→0

• Имеем неопределённость вида ( 1∞ ). Преобразуем основание так, чтобы оно

2 β
имело вид 1 + α(x), где α(x) – б.м. функция при x→ 0. Имеем cosβ =1−2sin 2	,

поэтому

	(			)	1			−2sin2
lim		cos	x		x = lim		1


x→0						x→0

									2		x
										−2sin
	1							1		−2sin	2
	1							1		x
x		x				2	x	−2sin2	x
x						2	x	−2sin2
			= lim	1	+	−2sin			2		=
2			= lim	1	+	−2sin	2		2		=
2			x→0				2

2 x

x 2

−2 sin

−2

lim

−

= ex→0

= sin

x~→0

= ex→0

= e

. •

9. Найти lim

x2 − 1

ln x

x→1

•Имеем неопределённость 0 . Сделаем замену x – 1 = t. Тогда x = 1 + t,

t→ 0 при x→ 1. Воспользуемся эквивалентностью б.м. ln(1+t) ~ t

при t→ 0.

Итак, lim

x2 − 1

= lim

( t + 1 )2 − 1

= lim

t 2 + 2t

= lim( t + 2 ) = 2 . •

ln x

ln( 1 + t )

x→1

t→0

10. Найти

lim

10cos2 x − 1

ln sin x

x→ 2

• Неопределённость вида

x −

= t , отсюда x =

+ t ,

. Сделаем замену

t→ 0 при x → π .

Воспользуемся формулой cos β = 1 − 2 sin2 β

и формулами

приведения:

lim		10cos2 x − 1	= lim
lim		ln sin x	= lim
x→	π	ln sin x	t→0
x→	2

2		π
cos		2	+t
10		2		− 1	= lim
	π				= lim
	π				t→0
ln sin			2	+ t
			2

10sin2 t − 1 ~ sin2 t ln10 ~ t 2 ln10

= lim t

ln10 = −2 ln10 . •

t→0

2 t

t→0

t 2

− 2 sin

~ − 2

−

t→0

2 t→0

11. Для функции

f ( x ) = arctg

найти точки разрыва,

если они существуют,

указать характер разрыва, построить схематический график функции.

•Данная функция определена, а, значит, и непрерывна x R\{0}. В точке

x= 0 функция разрывная, так как f(0) не определена.

Исследуем поведение функции в окрестности точки x = 0. Для этого вычислим односторонние пределы:

f ( 0 − 0 ) = lim

arctg

= −

π , так как

lim

= −∞ , а

lim arctgt = −

x→0−0

x→0−0 x

t→−∞

(см. график функции arctgx на рисунке 13

главы 2).

Аналогично, f ( 0 + 0 ) =

lim

arctg

= +

π .

x→0+0

Итак, односторонние пределы в точке x = 0 существуют, конечные, но не совпали. Значит, точка x = 0 является точкой разрыва 1-го рода. Скачок равен

f(0 + 0) – f(0 – 0) = π. Так как
lim	f ( x ) = lim arctg	1 =	1	= t , t →0 при x → ∞ = lim arctgt = 0,
x→∞	x→∞	x	x			t→0
то схематически график функции arctg					1	имеет вид:
то схематически график функции arctg					x	имеет вид:
					x

Рисунок 12

	1			,	x < 1

			1
x +			1
	2	,			1 ≤ x ≤ 2 найти точки разрыва, указать
12. Для функции f ( x ) = x		,			1 ≤ x ≤ 2 найти точки разрыва, указать
		1
					x > 2

e x−2 ,

характер разрыва, построить схематический график функции.

• Данная функция составная и определена x R \{−1}. Нельзя сразу сказать,

что она непрерывна для всех таких x. Разрывы могут быть в точках x = 1 и x = 2, где меняется её аналитическое выражение. Итак, подлежат исследованию точки

x = – 1, x = 1, x = 2.

Исследуем точку x = – 1.

Значение f(–1) не определено.

f ( −1 − 0 ) =

lim

= −∞ , так как x + 1 < 0, поэтому

lim

( x + 1 ) = − 0 .

+ 1

x→−1−0 x

x→−1−0

Аналогично, f ( −1 + 0 ) =

lim

= +∞ .

Итак,

точка x

= –1 является

x +

x→−1+0

точкой разрыва второго рода.

Исследуем точку x = 1.

f(1) = 12 = 1,

f ( 1 − 0 ) =

lim

f ( 1 + 0 ) =

lim

x2 = 1 .

x +

x→1−0

x→1+0

Итак, точка x = 1 является точкой разрыва первого рода.

Исследуем точку x = 2.

x2 = 4 ,

Имеем f(2) = 22 = 4,

f ( 2 − 0 ) =

lim

x→2−0

f ( 2 +0 ) =

lim

= t

= lim et = +∞ .

x−2

x − 2

x→2+0

t → +∞ при x → 2 +0

t→+∞

Итак, точка x = 2 – точка разрыва второго рода.

= e+0 = 1 + 0 ,

Так как lim

f ( x ) =

lim

= −0 ,

а lim

f ( x ) =

lim e

x−2

x→−∞

x→−∞ x +

x→+∞

то график данной функции имеет вид:

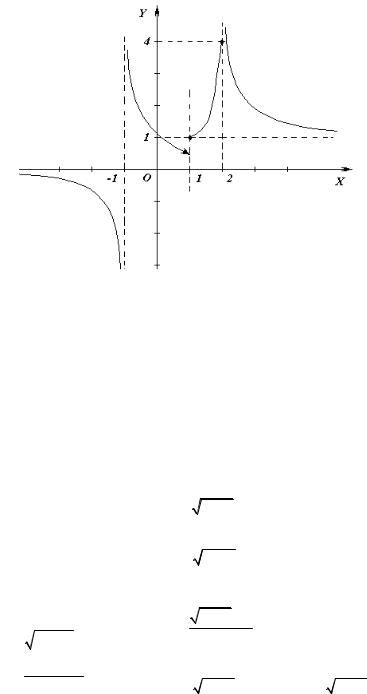
Рисунок 13

4.2 Задачи для самостоятельного решения

1. Вычислить пределы числовых последовательностей:

а)	lim	2 − 3n	;	б)	lim		( n + 2 )2 − ( n − 2 )2	;

	n→∞ 4 + 5n				n→∞		( n − 3 )2
в)	lim	2n +7 n		; г)	lim		2 + 4 + 6 + K + 2n			.
						1 + 3 + 5 + K + ( 2n −			1 )
	n→∞ 2n −7 n−1				n→∞

2. Вычислить пределы функций:

1) lim	x2	+ 3 x + 2		;	2) lim
	x3 +	2 x2	− x − 2
x→−1					x→1

	3 x + 1	2 x+3
4) lim		;
	3 x − 1
x→∞

7) lim	ln( 1 + x2 )	;
	1 + x2 − 1
x→0

10) lim 1 − sin3 x ; x→π2 cos2 x

5) lim

x→0

8) lim

x→0

11) lim

x→10

5 − x − 2	;
x3 − 1	;
x3 − 1
4 + x − 2			;
			;
arctg3 x
cos x − 1	;
sin2 2 x	;
lg x − 1		;
x − 9 − 1		;
x − 9 − 1

		2 x2		− 4	−x2
3)	lim				;
			2
		2 x		− 1
	x→∞

6) lim	sin7 x		;
6) lim			;
x→0	x2 +π x
	cos π x
9) lim	2		;
9) lim	2x−1 −	1	;
x→1	2x−1 −	1

12) lim		eπ x − 1		;
	3	1 + x −	1
x→0

2 − x ln( 2−x )

13) lim ;

x→1 x

14) lim	sin(π( x + 2 ))	; 15)	lim		esin 2 x − 1		.
	1 + x − 1					2 x
x→0			x→	π	ln
				2		π

3. Для данных функций найти точки разрыва, выяснить характер разрыва, построить схематический график:

1) f ( x ) =

;

2) f ( x ) = e

x ;

( 1 + x )

x , | x |≤ 1

0 ,

x ≤ 0

3) f ( x ) =

;

4) f ( x ) = e x , 0 < x < 2 ;

1, | x |>

x + 3, x ≥ 2

x ,

x < 1

5) f ( x ) =

;

6) f ( x ) =

− 3

x ≥ 1

1 − 2 x−1

− 3

Глава 4. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ ОДНОГО АРГУМЕНТА

1. ПОНЯТИЕ ПРОИЗВОДНОЙ

Переходим к изложению основ дифференциального исчисления. В качестве введения в дифференциальное исчисление рассмотрим задачу о скорости и задачу о касательной. Обе задачи исторически оказались связанными с формированием основного понятия дифференциального исчисления, получившего название произ-

водной.

1.1 Задача о скорости и задача о касательной

Задача о скорости. Материальная точка движется прямолинейно так, что в каждый момент времени t она находится на расстоянии S = f ( t ) от некоторой

выбранной в качестве начальной точки O (говорят, что задан закон движения

S= f ( t )). Найти скорость v движения точки в момент t0 .

Вмомент времени t0 пройденное расстояние равно f ( t0 ) = S0 , а в момент времени t0 + ∆t расстояние равно f ( t0 + ∆t ) = S1 . Таким образом, за промежу-

ток времени от t0 доt0 + ∆t точка пройдет путь ∆S = S1 −S0 = f (t0 +∆t )− f (t0 ). Средняя скорость движения материальной точки за указанный промежуток

времени равна ∆S = f ( t0 + ∆t ) − f ( t0 ) . Средняя скорость движения зависит не

∆t ∆t

только от выбранного момента времени t0, но и от длительности рассматриваемого промежутка времени ∆t. Чем меньше величина ∆t, тем точнее средняя скорость «характеризует» это движение в момент времени t0. Поэтому предел средней скорости движения при стремлении ∆t к нулю называют скоростью движения точки в данный момент времени t0 (мгновенной скоростью):

v( t0 ) =	lim	∆S	= lim	f ( t0	+ ∆t ) − f ( t0	)	.
		∆t			∆t
	∆t→0		∆t→0

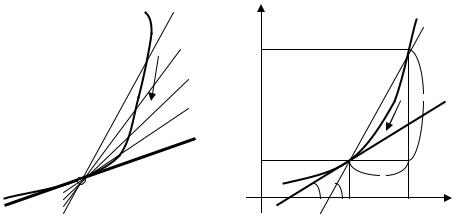
Задача о касательной. Пусть имеется кривая и лежащая на ней некоторая точка M. Возьмём на этой кривой любую другую точку N и будем перемещать её по кривой, неограниченно приближая к точке M (то есть, чтобы расстояние между ними стремилось к нулю). При этих условиях секущая MN, вообще говоря, меняет своё положение, вращаясь вокруг точки M (рисунок 1). Если существует прямая MT, являющаяся предельным положением секущей MN при неограниченном приближении точки N по кривой к точке M, то эта прямая называется касательной к кривой в точке M. Следует иметь в виду, что кривая в её точке M может и не иметь касательной.

Рассмотрим некоторую плоскую кривую с уравнением y = f ( x ) и точку

M (x0 , f ( x0 )) этой кривой (рисунок 2). Пусть кривая в точке M имеет невертикальную касательную MT. Напишем уравнение этой касательной.

Значению аргумента	x0 + ∆x	соответствует значение функции
f ( x0 + ∆x ) = f ( x0 ) + ∆y	и, значит, точка N ( x0 + ∆x; f ( x0 + ∆x )) кривой.

Здесь ∆x – произвольное приращение аргумента x = x0 , а ∆y = f( x0 +∆x)− f( x0 )

– соответствующее приращение функции.

	Y		y=f(x)
			y=f(x)
N	f (x0+∆x)		N
			∆y	T
	T
	f(x0)	M
M		α β	∆x
	0	x0	x0+∆x	X
Рисунок 1		Рисунок 2

Пусть теперь ∆x→ 0, тогда точка N по кривой стремится к точке M, секущая MN, меняя своё положение, будет стремиться занять положение касательной MT к кривой в точке M. Обозначим через β угол наклона к оси OX секущей MN, а

через α – угол наклона касательной к кривой в точке M. Если ∆x→ 0, то β→α и, значит,

tgβ → tgα. Но tgβ =	∆y	, следовательно, tgα = lim	∆y .
	∆x	∆x→0	∆x

Уравнение касательной MT – прямой, проходящей через точку M( x0 , f ( x0 ))

с угловым коэффициентом k = tgα , запишется в виде
y −	f ( x	) = k( x − x ) = lim		∆y ( x − x ) .
	0	0	∆x→0	∆x	0
			∆x→0	∆x

Итак, если сопоставить операции, которые осуществлялись при решении рассмотренных задач, то легко заметить, что в обоих случаях по существу делалось одно и то же: приращение функции делилось на приращение независимой переменной и затем вычислялся предел их отношения. Таким путём приходим к основному понятию дифференциального исчисления – к понятию производной.

1.2 Определение производной

Пусть функция y = f ( x ) определена в некоторой окрестности точки x. Дадим

аргументу x приращение ∆x (при этом предполагается, что точка x + ∆x принадлежит области определения функции). Тогда функция получит приращение

∆y = f ( x + ∆x ) − f ( x ) .

Производной функции f ( x ) в точке x называется предел отношения прира-

щения функции к приращению аргумента при стремлении приращения аргумента к нулю, если этот предел существует и конечен.

		Производная		функции y = f ( x ) в		точке x обозначается символами:		y′,
	′		dy	df ( x )

f		( x ) или dx ,		dx .
f		( x ) или dx ,		dx .
		Итак, по определению				f ( x + ∆x ) − f ( x )
					f ′( x ) = lim	f ( x + ∆x ) − f ( x )	.	(1)
					f ′( x ) = lim		.	(1)
					∆x→0	∆x
		Производная		f ′( x ) является функцией аргумента x, поскольку, если для дан-

ного значения аргумента x существует предел отношения (1), то только один. При конкретных числовых значениях аргумента x производная – число. В случаях, когда может возникнуть сомнение относительно переменной, по которой взята про-

изводная, эта переменная указывается в виде значка внизу: y / , f / ( x			0	) .
x	x
Рассматривая задачу о скорости, мы получили, что v = lim	∆S	,	т.е.		v =	dS	.
	∆t
∆t→0						dt

Отсюда следует механический смысл производной: скорость v есть производная от пройденного пути S по времени t.

Если слово «скорость» понимать в более широком смысле, то можно производную функции y = f ( x ) по x считать скоростью изменения переменной y в точке

x. Поэтому понятие производной находит широкое применение при изучении скорости течения различных процессов (например, скорость охлаждения нагретого тела; скорость осуществления работы – мощность; скорость обесценивания оборудования и т.п.).

Из рассмотренной задачи о касательной следует, чтоtgα = lim	∆y	, т.е.
∆x→0	∆x

tgα = y′ . Отсюда следует геометрический смысл производной: производная функции y = f ( x ) в точке x равна угловому коэффициенту k = tgα касательной в точке M( x, f ( x )) графика функции.

На основании ранее приведённых рассуждений получаем, что уравнение невер-

тикальной касательной к кривой y = f ( x ) в её точке M( x0 ,	f ( x0 )) можно
записать в виде
y − f ( x0 ) = f ′( x0 )( x − x0 ).	(2)
97

Нормалью к кривой в её точке M называется прямая, проходящая через точку M перпендикулярно касательной к кривой в этой точке. Так как у двух взаимно перпендикулярных прямых угловые коэффициенты обратно пропорциональны и

отличаются знаком, то уравнение нормали		к кривой		y = f ( x )	в точке
M ( x0 , f ( x0 )) имеет вид
y − f ( x ) = −	1		( x − x	) ,	(3)
y − f ( x ) = −			( x − x	) ,	(3)
0	f ′( x0	)	0
	f ′( x0	)

если f ′( x0 ) ≠ 0 .

Пример 1. Найти производную функции y = x3 .

•В этом случае

∆y =( x +∆x )3 −x3 = x3 +3x2∆x+3x(∆x )2 +(∆x)3 −x3 =(3x2 +3x∆x+(∆x )2 )∆x,

∆y	= 3 x2	+ 3 x∆x + ( ∆x )2 , lim	∆y	= 3 x2 .
∆x		∆x→0	∆x
Следовательно, y′ = 3 x2		. •

Пример 2. Написать уравнение касательной и нормали к кривой y = x в точ-

ке M ( 1; 1 ) .

• Функция y = x определена и непрерывна при 0 ≤ x < +∞ . Составим при-

ращение функции ∆y = x + ∆x − x . Для отыскания предела отношения при-

ращений функции и аргумента переносим иррациональность в знаменатель с последующим сокращением:

lim

∆y

lim

x + ∆x − x

= lim

(

x + ∆x − x ) ( x + ∆x + x )

∆x ( x + ∆x +

x )

∆x

∆x→0

= lim

x + ∆x − x

= lim

x )

∆x→0 ∆x (

x + ∆x +

∆x→0

+ ∆x +

x 2 x

Итак,

y′ = (

x )′ =

точке M ( 1;

1 ) :

Вычислим

угловой

коэффициент

касательной в

′

2 .

k = y ( 1 ) =

Уравнения касательной и нормали будут иметь вид (согласно (2) и (3) ):

y − 1 =

( x − 1 ) , y − 1 = −2( x − 1 ) или x − 2 y + 1 = 0 , 2 x + y − 3 = 0 .

•

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 2310 11 12 13 14 15 16 17 18 19 20 21 22 23 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.02.20151.73 Mб316matem-up1.pdf
#
14.02.201554.78 Кб17Matematika-i-statistika-12-RiSO-B.doc
#
14.02.2015543.23 Кб30matematika_ekzamen - .doc
#
14.02.20152.69 Mб320matematika_metod_posobie.docx
#
14.02.20151.69 Mб232Matematika_ryad.doc
#
14.02.20152.17 Mб54Matematika_Zaytsev_ch2.pdf
#
14.02.20158.95 Mб92matematike_fepo_s_otvetami.doc
#
24.08.20193.22 Mб24materialoved.doc
#
14.02.2015899.5 Кб40mcad_pract.pdf
#
14.02.2015203.78 Кб25mech.doc
#
15.11.2019323.76 Кб7Meeting clients.docx