Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Алтайский государственный технический университет им. И.И.Ползунова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Matematika_Zaytsev_ch2

.pdf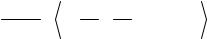

Скачиваний:

Добавлен:

14.02.2015

Размер:

2.17 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 2312 13 14 15 16 17 18 19 20 21 22 23 > Следующая >>>

Этот же приём удобен и при дифференцировании показательно-степенной функции y = [u( x )]v( x ) .

Так как ln y =v( x )lnu( x ), то

y′

′

lnu +v

′

или y

′

lnu +

vu′

= v

Пример 9. Найти производную функции y = x x .

● Так как ln y = x ln x , то

y′

= ln x + x

y′ = (ln x + 1 ) x x . ●

4. Найдём производные функций y = sin x и y = cos x .

Для функции y = sin x имеем

∆x

∆y

∆x

sin

∆x

∆y = sin( x + ∆x ) − sin x = 2 sin

cos x +

= 2cos x

∆x

∆y

∆x

sin ∆x

∆x

y′ = lim

= 2 lim

sin

при∆x →0 =cos x

∆x

cos x +

lim

∆x→0

∆x

Итак,

′

= cos x .

(17)

(sin x )

Так как

то, применяя правило дифференцирования

y = cos x = sin

− x ,

′

сложной функции, находим y′ = cos

− x

− x = sin x ( −1 ) = − sin x .

Итак,

′

= −sin x .

(18)

(cos x )

5. Найдём производные функций y = tgx и y = ctgx .

Представляя функцию в виде

y = tgx =

sin x

, используя правило нахождения

cos x

производной частного и формулы (17), (18), получим

sin x

′

(sin x )′ cos x − sin x (cos x)′

cos2 x + sin2 x

y′ =

, т.е.

cos2

cos x

(tgx )′ =

(19)

cos2 x

Аналогично найдём

109

1
(ctgx )′ = − sin2 x .	(20)

6. Рассмотрим обратные тригонометрические функции. Для отыскания производных этих функций будем использовать правило дифференцирования обратной функции.

Для функции y = arcsin x имеем

x = sin y , x y/ = cos y =

1 − sin2 y =

1 − x2 .

Здесь перед корнем взят знак плюс, Так как по определению функции

y = arcsin x

имеем −π

≤ y ≤ π , поэтому cos y ≥ 0 . Отсюда находим

yx/

x y/

1 − x2

Итак,

′

(21)

(arcsin x )

1 − x2

Так как имеется тождество arcsin x + arccos x = π , то

′

− arcsin x

(22)

(arccos x )

= −(arcsin x ) = −

Для функции y = arctgx

1 − x2

имеем

x = tgy , x y/ =

= 1 + tg2 y = 1 + x2 ,

yx/

cos2 y

xy/

1 + x2

Следовательно,

′

= 1 + x2 .

(23)

( arctg x )

Из тождества arctgx + arcctgx = π

следует, что

′

− arctg x

= −

(24)

( arcctg x )

= −( arctg x )

+ x

В заключение приведём таблицу полученных правил и формул дифференцирования, которую рекомендуется запомнить.

Основные правила дифференцирования:

1) (C )	′		C − const ;				′	′	+ v	′	;
1) (C )	= 0 ,		C − const ;			2) ( u + v )		= u	+ v		;
	′	′		′	;	′		′
3) ( u v )		= u v + uv			;	4) ( Cu )	= Cu ;
						110

		′				′		′
	u					′		′
5)	u		=			u v − uv			;

							v2
	v						v2
7)	x y/	=			1		;
7)	x y/	=		yx/			;
				yx/

6) yx/ = yu/ ux/ ;
			/
y /		=	yt
y /		=	xt / .
8) y = y( t ) , x = x( t )	x		xt / .

x = x( t )

Производные основных элементарных функций:

1) ( xa )′ = axa−1 ;

2) (a x )′ = a x lna ;

′

(loga x ) =

;

4) (sin x ) = cos x ;

lna

(cos x )′ = − sin x ;

6) (tgx )′ =

;

cos2 x

(ctgx )′ = −

;

8) (arcsin x )′

;

sin2 x

1 − x2

(arccos x )′

= −

;

10) (arctgx )′ =

;

1 − x2

1 + x2

11)

(arcctgx)′

= −

1 + x2

Отметим, что, пользуясь этой таблицей, можно найти производную любой элементарной функции, т.е. функции, которая получается из основных элементарных функций с помощью конечного числа алгебраических действий и применением конечного числа операций вычисления функции от функции.

4. ПОНЯТИЕ ДИФФЕРЕНЦИАЛА

4.1 Определение дифференциала

Рассмотрим важное в теории и для приложений понятие дифференциала. Пусть

функция y = f ( x ) дифференцируема, т.е. существует lim	∆y	= f ′( x ) . Тогда
∆x→0	∆x
приращение функции имеет вид (см. (5)):
∆y = f ′( x ) ∆x +α ∆x ,		(25)

где lim α = 0 .

∆ x→0

В случае f ′( x ) ≠ 0 первое слагаемое f ′( x )∆x , линейное относительно ∆x ,

имеет по отношению к ∆x тот же порядок малости, а второе слагаемое α ∆x – высший порядок малости по сравнению с ∆x , так как

111

lim	f ′( x )∆x	= f ′( x ) ≠ 0 ,	lim	α ∆x	=	lim α = 0 .
	∆x			∆x
∆x→0			∆x→0			∆x→0

Поэтому первое слагаемое f ′( x )∆x является главной частью приращения функции. В случае f ′( x ) = 0 главная часть приращения функции равна нулю. Во всех

случаях при малых ∆x приращение функции мало отличается от своей главной части. Эту главную часть приращения функции, линейную относительно приращения аргумента, называют дифференциалом функции и обозначают символом dy :

dy = f ′( x ) ∆x .	(26)
Равенство
∆y = dy +α ∆x ,	(27)

непосредственно следующее из соотношений (25) и (26), показывает, что дифференциал функции отличается от её приращения на слагаемое, являющееся бесконечно малой высшего порядка относительно ∆x . Отсюда следует приближённое выражение для приращения функции:

∆y ≈ dy или f ( x + ∆x ) ≈ f ( x ) + f ′( x )∆x .		(28)
Абсолютная погрешность при такой замене равна	∆y − dy		и является при

∆x → 0 бесконечно малой более высокого порядка, чем ∆x .

Когда вычисление значения функции y = f ( x ) и её производной в некоторой

точке x оказывается более простым, чем вычисление значения функции в другой точке x + ∆x , то можно воспользоваться приближённым вычислением этого значения f ( x + ∆x ) по формуле (28) (если ∆x мало).

Пример 9. Найти приближённое значение функции	f ( x ) = x3 − 3 x2 + 5 x + 8
при x = 3,02 .
● При x = 3 значение функции и её производной	f ′( x ) = 3 x2 − 6 x + 5 легко

вычисляются: f ( 3 ) = 23 , f ′( 3 ) = 14 . Положим ∆x = 0 ,02 , тогда x + ∆x = 3 + 0 ,02 = 3,02

и, согласно (28), получим

f ( 3,02 ) ≈ f ( 3 ) + f ′( 3 )∆x = 23 + 14 0 ,02 = 23,28 .

При точном подсчёте получается f ( 3,02 ) = 23,282408 . Абсолютная ошибка

0 ,002408 .●

Замечание. Если формулу (26) применить к функции, равной аргументу (y = x), то получим dy = dx = 1 ∆x = ∆x . Поэтому естественно под дифференциалом ар-

гумента понимать его приращение. В силу этого, формулу (26) можно записать в виде

dy = df ( x ) = f ′( x )dx .

(29)

112

Эта формула позволяет считать производную отношением дифференциалов:

f ′( x ) =	df ( x )	или y′ =	dy
				.
	dx		dx

Практически дифференциал находят по формуле (29), используя свойства производных и формулы производных простейших элементарных функций. Например,

d (	x ) = (	x )′ dx =		1	dx	, d (ln x) = (ln x)′ dx =	1	dx и т. д.
		2		x			x

4.2 Свойства дифференциала

Отметим основные свойства дифференциала функции. 1) dC = C′dx = 0 dx = 0 , где С - постоянная;

2)d (u( x )+v( x )) =(u( x )+v( x ))′dx =(u′+v′)dx = u′dx +v′dx = du +dv ;

3)d (u( x ) v( x )) =(u v)′dx =(u′v + uv′)dx = u′dx v + u v′dx = du v + u dv ;

4)d (C u( x )) = (C u( x ))′ dx = Cu′( x )dx = Cdu ;

′

u u

v − uv

v du − u dv

dx v − uv dx

dx =

;

v v

6) дифференциал сложной функции

y (u( x )):

′

/ /

dy = y dx = yu ux dx

= yu du .

Этот результат мы могли сразу получить, если бы переменная u была бы неза-

висимой переменной. Таким образом, форма записи дифференциала функции будет неизменной независимо от того, будет ли переменная u независимой перемен-

ной или функцией другой переменной x. Указанный результат выражает так назы-

ваемое свойство инвариантности (неизменности) формы дифференциала функции.

Y					7) Геометрический		смысл
					7) Геометрический		смысл
		N			дифференциала функции.
		N		T	Пусть	точка M на	графике
			∆y	T	функции	y = f ( x ) соответствует
					функции	y = f ( x ) соответствует
					значению аргумента x, а точка N –
			K		значению аргумента x, а точка N –
y=f(x)	M	α	dy		значению	аргумента	x + ∆x ,
		∆x	P		прямая MT–касательная к графи-
	α			X	ку y = f ( x ) в точке		M, α –
0	x		x+∆x	X	угол между касательной и осью
	Рисунок 6				OX (рисунок 6).
	Рисунок 6
				113

Приращение функции равно ∆y = NP . Из прямоугольного ∆ MKP получа-

ем KP = tgα ∆x = f ′( x )∆x = dy .

Таким образом, дифференциал dy функции y = f ( x ) в точке x равен приращению ординаты точки касательной к графику этой функции с точкой касания M (x, f ( x )) , соответствующему приращению ∆x аргумента x.

5. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ

5.1 Производные высших порядков

Производная y′ = f ′( x ) функции y = f ( x ) сама является некоторой функ-

цией аргумента x. Поэтому по отношению к ней снова можно ставить вопрос о существовании и нахождении производной.

Производная от производной данной функции называется производной второго порядка (или второй производной) этой функции и обозначается символом y′′ ,

или y( 2 ) , т.е. y′′ = ( y′)′.

Аналогично, производная от второй производной называется производной третьего порядка (или третьей производной): y′′′ = ( y′′)′ и т.д., производная

n-го порядка (или n-я производная): y( n ) = ( y( n−1 ) )′ .

Следовательно, производная n–го порядка может быть найдена в результате n последовательных дифференцирований функции.

Замечание. Ранее было выведено правило дифференцирования функции, заданной параметрически (см. формулу (13)). Тогда вторая производная yxx// , как

производная по x от первой производной, определится формулой, которая является следствием формулы (13):

yxx//	= ( yx/ )	x/	=	( yx/	) t/
					/ .	(30)
				xt

Для отыскания третьей производной поступаем аналогично, так как вторая производная снова оказывается функцией параметра t. То же будет верно и для последующих производных.

Пример 10. Найти производную третьего порядка в точке x = 1 функции

y= ln( 2x − 1 ) .

●Имеем y′ = 2x1− 1 ( 2 x − 1 )′ = 2 x2− 1 = 2( 2 x − 1 )−1 ,

y′′ = 2 ( −1 )( 2 x − 1 )−2 ( 2x − 1 )′ = −4( 2 x − 1 )−2 ,

114

′′′

−3

′

−3

= −4 ( −2 )( 2 x − 1 )

( 2 x − 1 ) = 16( 2 x −

1 )

Следовательно, y′′′( 1 ) = 16( 2 1 − 1 )−3 = 16 .

●

Пример 11. Найти производную yxx//

, если

x = cos t ,

y = sin t .

● Вначале найдём xt/ = − sin t ,

yt/

= cos t , yx/ =

yt/

cos t

= −ctgt . От-

xt/

− sin t

(−ctgt ) t/ =

сюда, согласно формуле (30), получаем:

yxx// =

sin2 t

= −

●

− sin t

sin3 t

Вторая

производная имеет простой

механический

смысл.

Если

функция

S = S( t )

описывает закон прямолинейного движения материальной точки, то

первая производная

S′( t ) есть скорость точки в момент времени t, а вторая про-

изводная

S′′( t ) = (S′( t ))′ = v′( t )

равна скорости изменения скорости, т.е. уско-

рению точки в этот момент.

5.2 Дифференциалы высших порядков

Предварительно отметим следующее: dy = f ′( x )dx зависит от двух переменных: x и dx = ∆x , которые между собой независимы.

Дифференциалом второго порядка (вторым дифференциалом) от функции y = f ( x ) (его обозначают d 2 y ) называется дифференциал от её дифференциа-

ла, рассматриваемого как функция только от аргумента x (т.е. при постоянном dx ). Найдём его выражение

d 2 y = d( dy ) = d ( f ′( x )dx) = ( f ′( x )dx)′ dx = f ′′( x )( dx )2 .

Аналогично вводятся дифференциалы третьего, четвёртого и более высоких порядков. Вообще, дифференциалом n-го порядка называется дифференциал от диф-

ференциала ( n − 1 ) - го порядка. Аналогично предыдущей формуле, получим
d n y = d (d n−1 y) = f ( n )( x )( dx )n .	(31)
Замечание. Свойством инвариантности формы дифференциал n -го порядка
(при n > 1 ) не обладает. В самом деле, если y = f ( u ) , u = u( x ) , то

d2 y = d( dy ) = d ( f ′( u )du) = d ( f ′( u ))du + f ′( u )d( du ) = f ′′( u )( du )2 + f ′( u )d2u

(здесь du ≠ const для произвольной функции u = u( x ) ).

Пример 12. Вычислить d 3 y для функции y = ln x .
● Последовательно дифференцируя, получим
1			2			2
y′ =		= x−1 , y′′ = −x−2	, y′′′ = 2 x−3 =		, т. е. d 3 y = y′′′( dx )3 =		( dx )3 .●
	x			x3		x3
			115

6.ЗАДАЧИ

6.1Задачи с решениями

1. Пользуясь только определением производной, найти f ′( x ) для функций:

1) f ( x ) = 5 x2 − 2 x + 1 ;

2) f ( x ) = cos 3 x .

● 1) Используем определение производной:

′

f ( x +∆x )− f ( x )

[5( x +∆x )2 −2( x +∆x )+1] −[5x2 −2x +1]

f ( x ) = lim

= lim

∆x

∆x→0

= lim

5 x2 + 10 x∆x + 5( ∆x )2 − 2 x − 2∆x + 1 − 5 x2 + 2 x − 1

∆x→0

∆x

= lim

10 x∆x − 2∆x + 5( ∆x )2

= lim ( 10 x − 2 + 5∆x ) = 10 x − 2 .

∆x

∆x→0

2) Аналогично, имеем:

′

cos 3( x + ∆x ) −cos 3x

α + β

α − β

f ( x ) = lim

= cosα −cos β = −2 sin

sin

∆x

∆x→0

−2 sin( 3 x +

∆x )sin

∆x

sin( 3 x +

∆x )

sin

∆x

lim

= −2 lim

lim

∆x

∆x→0

∆x

= −2 sin 3 x

= −3 sin 3 x . Здесь учитывалось, что синус – непрерывная функция

sin

∆x

∆x при ∆x → 0 . ●

2. Найти односторонние производные							f ′( 1 − 0 ) , f ′( 1 + 0 ) (пользуясь только
их определением) для функции
			2 x				,	x ≤ 1
			f ( x ) =				+ 3 x , x > 1.
			−x2				+ 3 x , x > 1.

● Данная функция непрерывна x R (почему?). Имеем
f ′( 1 − 0 ) =	lim		f ( 1 + ∆x ) − f ( 1 )		=
f ′( 1 − 0 ) =	lim				=
	∆x→0−0		∆x
=	так как 1 + ∆x < 1 при			∆x → 0 − 0 , то						f( 1 + ∆x) = 2( 1 + ∆x ) =
=	lim	2( 1 + ∆x ) − 2 1		=			lim	2∆x	=	2 ,
=	lim		∆x	=			lim		=	2 ,
	∆x→0−0		∆x		∆x→0−0			∆x
f / ( 1 + 0 ) = lim			f ( 1 + ∆x ) − f ( 1 )			=
f / ( 1 + 0 ) = lim						=
	∆x→0+0		∆x
				116

= так как 1 + ∆x > 1 при ∆x → 0 + 0, то f( 1 + ∆x) = −( 1 + ∆x )2 + 3( 1 + ∆x ) =

lim

−( 1 + ∆x )2 + 3( 1 + ∆x )− 2 1 =

lim

∆x −( ∆x )2

lim ( 1 −∆x ) = 1 .

∆x→0+0

∆x

∆x→0+0

∆x

∆x→0+0

Заметим, что

f ′( 1 − 0 ) ≠ f ′( 1 + 0 ) , поэтому f ′( 1 ) не существует. ●

3. Найти производную функции y = 3 1 − x2

+ x3 cos x .

● Используя правила дифференцирования суммы и произведения двух функ-

ций, получаем:

y /

= (3 1 − x2 )′ + ( x3 )′ cos x + x3 (cos x)′ .

Производная (3 1 − x2 )′

находится как производная сложной функции, задан-

f ( u ) = 3 u = u

u = 1 − x2 .

ной цепочкой равенств:

Так как fx/

fu/

ux/

−

(−2 x), то (3

1 − x2 )

′

−2 x

3 3

(1 − x2 )

Производные ( x

)

′

= 3 x

′

= −sin x – табличные.

(cos x )

Окончательно,

′

= −

2 x

+ 3 x

cos x − x

sin x . ●

3 3

(1 − x2 )2

4. Найти производную функции y =

101−x

− (arcsin 2 x )2 .

cos 5 x

● Имеем:

101−x

′

(

)

′

−

(arcsin 2 x )

cos 5 x

(101−x )′ cos 5 x − 101−x (cos 5 x)′

− 2 arcsin 2 x (arcsin 2 x)′ =

(cos 5 x)2

101−x ln10 (1 − x)′ cos 5 x − 101−x (− sin5 x) (5 x)′

−

cos2 5 x

−2 arcsin 2 x

(2 x)′ =

1 − (2 x)2

117

=	−101−x ln10 cos 5 x + 5 101−x sin5 x			−	4 arcsin 2 x	. ●
=	cos2 5 x			−	1 − 4 x2	. ●
	cos2 5 x				1 − 4 x2
5. Найти y / (−1) , если y =		x	10
			.
		2 x + 1	.
		2 x + 1

● Вычислим вначале производную в произвольной точке x:

x 9

x ′

x′(2 x + 1) − x (2 x + 1)′

y′ = 10

(2 x + 1)2

2 x + 1

2 x +

x 9

1 (2 x +

1) − x 2

10 x9

= 10

(2 x + 1)2

(2 x + 1)11

2 x + 1

При x = −1 получим y′( −1 ) =

10(

−1 )9

= 10 . ●

( 2 ( −1 ) +

1 )

6. Найти производную функции

y = 1

● Данная функция является показательно-степенной (и показатель, и основание

– переменные величины). Логарифмируем эту функцию:

			1 x				1
ln y = ln	1	+		= x ln	1	+		.

			x				x

Находим производные левой и правой частей:

(ln y)′

′

y′ = x′ ln

1 +

+ x ln

1 +

1 ′

= ln 1

+ x

1 +

= ln

−

Следовательно,

y′ = y

ln 1 +

−

= 1

−

. ●

x +

+ 1

7. Уравнение x3 + ln y = x2e y

определяет y как неявную функцию от x. Найти

y′ при x = 0 .

● Дифференцируя по x левую и правую части равенства и учитывая, что y = y( x ) , имеем:

118

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 2312 13 14 15 16 17 18 19 20 21 22 23 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.02.20151.73 Mб316matem-up1.pdf
#
14.02.201554.78 Кб17Matematika-i-statistika-12-RiSO-B.doc
#
14.02.2015543.23 Кб30matematika_ekzamen - .doc
#
14.02.20152.69 Mб320matematika_metod_posobie.docx
#
14.02.20151.69 Mб232Matematika_ryad.doc
#
14.02.20152.17 Mб54Matematika_Zaytsev_ch2.pdf
#
14.02.20158.95 Mб92matematike_fepo_s_otvetami.doc
#
24.08.20193.22 Mб24materialoved.doc
#
14.02.2015899.5 Кб40mcad_pract.pdf
#
14.02.2015203.78 Кб25mech.doc
#
15.11.2019323.76 Кб7Meeting clients.docx