
Matematika_Zaytsev_ch2
.pdf
k и b , то прямая L : y = kx + b будет двусторонней наклонной асимптотой (при x → ∞ ).
Замечание. Если хотя бы один из пределов в (14) не существует или бесконечен, то наклонной асимптоты нет.
Пример 21. Найти асимптоты графика функции |
y = |
e x |
. |
|
|||
x |
x = 0 |
||||||
|
|
|
|
|
|||
● Функция определена и непрерывна при всех x , |
за исключением |
||||||
( x = 0 – точка разрыва). Так как lim |
e x |
= ±∞ , то прямая с уравнением |
x = 0 |
||||
x |
|||||||
x→0±0 |
|
|
|
|
|
||
(ось OY ) – вертикальная асимптота (двусторонняя). |
|
|
|
||||
Ищем наклонные асимптоты в виде y = kx + b : |
|
|
|
|
|||
k = |
lim |
y |
= |
lim |
e x |
|
∞ |
= |
правило Лопиталя = |
lim |
e x |
|
∞ |
= |
|
|
= |
|
|
= |
|
||||||||
|
x→+∞ x |
|
x→+∞ x2 |
|
∞ |
|
|
x→+∞ 2 x |
|
∞ |
|
|||
= правило Лопиталя = lim |
e x |
= +∞ . Так как |
k = +∞ , то правой |
|
2 |
||||
x→+∞ |
|
|
наклонной асимптоты нет. Ищем левостороннюю наклонную асимптоту:
k = |
lim |
y |
|
lim |
e x |
|
+0 |
= +0 , |
|
|
= |
|
= |
|
|
||||
|
|
|
|||||||
|
x→−∞ x |
|
x→−∞ x2 |
|
+∞ |
|
|||
|
e x |
|
|
|
|
e x |
|
|
+0 |
|
||
b = lim ( y − kx ) = |
lim |
|
− 0 |
x |
= |
lim |
|
= |
|
|
|
= −0 . |
|
|
|
||||||||||
x→−∞ |
|
x |
|
|
|
x→−∞ x |
|
|
|
|||
x→−∞ |
|
|
|
|
|
−∞ |
|
|||||
Коэффициенты k и b найдены, поэтому прямая |
y = kx + b = 0 x + 0 = 0 , т.е. |
|||||||||||
y = 0 (ось OX ) является левосторонней асимптотой (горизонтальной, частный
случай). Проведённое исследование знака числа b говорит о том, что график функции асимптотически приближается к оси OX снизу. ●
2.5 План исследования функции и построение её графика
Исследование функции и построение её графика рекомендуется проводить по следующей схеме.
1)Найти область определения функции.
2)Исследовать функцию на непрерывность. Найти точки разрыва функции и её односторонние пределы в этих точках.
3)Определить асимптоты графика и поведение функции на границе области определения.
4)Выяснить, является ли функция чётной, нечётной, периодической. При наличии какого-либо из этих свойств можно использовать симметрию при построении графика.
147
5)С помощью производной первого порядка найти промежутки возрастания и убывания, найти экстремумы функции.
6)С помощью производной второго порядка найти промежутки выпуклости и вогнутости графика функции, точки перегиба.
7)Используя результаты исследования, построить график функции. При необходимости можно дополнительно найти значения функции в некоторых точках из тех промежутков, для которых предыдущие пункты исследования дали недостаточно информации. Их роль – проверка и уточнение построенного графика. Можно определить точки пересечения графика с осями координат, а также посмотреть,
какой угол составляет касательная графика с осью OX в некоторых точках графика и т.д.
Пример 22. Исследовать функцию f ( x ) = |
x3 |
|
|
и построить её график. |
|
2( x + 1 )2 |
||
● Следуем предложенной схеме исследования функции.
1)Функция определена при всех значениях x , кроме x = −1 .
2)Выясним характер разрыва функции при x = −1 . Для этого рассмотрим односторонние пределы функции в точке x = −1 :
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|||||
|
|
lim |
|
|
|
|
|
|
|
|
= |
|
|
|
= −∞ , |
lim |
|
|
|
|
|
|
|
|
= |
|
|
= −∞ . |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2( x + |
1 )2 |
+0 |
|
|
|
||||||||||||||||||||||||||
|
|
x→−1−0 2( x + 1 )2 |
|
+0 |
|
|
|
|
|
x→−1+0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Полученный результат говорит о том, что точка |
x = −1 является точкой разрыва |
||||||||||||||||||||||||||||||||||||||||||||
2-го рода для данной функции, |
а прямая с уравнением x = −1 – вертикальной |
||||||||||||||||||||||||||||||||||||||||||||
асимптотой графика функции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
3) |
Ищем наклонные асимптоты: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
k = |
lim |
f ( x ) |
|
lim |
|
|
x2 |
|
|
|
|
|
|
∞ |
= lim |
|
|
|
2x |
|
|
∞ |
|
lim |
2 |
= 0,5 |
, |
||||||||||||||||||
|
|
|
|
= |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
= |
|
|
= |
|
|
|
||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
x→±∞ |
|
|
x→±∞ 2( x + 1 )2 |
|
|
x→±∞ 4( x + 1 ) |
|
∞ |
|
x→±∞ 4 |
|
|
|
|
|||||||||||||||||||||||||||||||
b = lim ( f ( x ) − kx) = |
|
|
|
|
|
|
x |
3 |
|
|
|
|
x |
|
1 |
|
|
|
|
x |
3 |
− x( x + |
1 ) |
2 |
|
|
|||||||||||||||||||
lim |
|
|
|
− |
= |
|
lim |
|
|
|
= |
|
|||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||||||||||
|
x→±∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2( x + |
|
|
|
2 |
|
2 x→±∞ |
|
( x + 1 ) |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
x→±∞ |
1 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
1 |
lim |
−2x2 |
− x |
|
|
∞ |
|
1 |
|
lim |
−4x −1 |
|
|
|
∞ |
|
|
1 |
lim |
|
−4 |
= −1 . |
|
|
|
|
||||||||||||||||||
= |
|
|
|
|
|
|
= |
|
= |
|
|
|
|
|
|
|
|
= |
|
= |
|
|
2 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
2 x→±∞ ( x +1)2 |
|
|
∞ |
|
2 x→±∞ 2( x +1) |
|
|
|
∞ |
|
|
2 x→±∞ |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Обратим внимание на то, что полученные результаты одинаковы как при
x → +∞ , так и при x → −∞ . Из существования этих конечных пределов следует,
что график функции имеет двустороннюю наклонную асимптоту |
y = 0 ,5 x − 1 . |
|||||||
4) Чётной или |
нечётной |
функция |
f ( x ) не является, так как |
|||||
f ( −x ) = |
|
( −x )3 |
= |
−x3 |
|
и видно, что |
f ( −x ) ≠ f ( x ) и |
f ( −x ) ≠− f ( x ). |
|
2 |
2 |
||||||
2( |
−x +1) |
2( x −1) |
|
|
|
|||
|
|
|
|
|
|
148 |
|
|

Периодической функция тоже не является, так как среди элементарных функций периодическими могут быть только тригонометрические функции.
5) Вычислим производную 1-го порядка: |
|
|
|
|
|
|
|||||||||
|
x3 |
|
′ |
|
1 3 x2 |
( x + 1 )2 − x3 2( x + 1 ) |
|
1 x2 ( x + 3 ) |
|
||||||
f ′( x ) = |
|
|
|
= |
|
|
|
|
|
= |
|
|
|
|
. |
|
|
|
|
|
4 |
|
|
3 |
|
||||||
|
2( x + 1 ) |
2 |
|
2 |
|
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
( x + 1 ) |
|
|
( x + 1 ) |
|
|||||
Приравнивая f ′( x ) нулю, получим критические точки 1-го рода:
1x2 ( x + 3 ) = 0 x2 ( x + 3 ) = 0 x1 = 0 , x2 = −3 .
2( x + 1 )3
|
|
|
|
Кроме того, |
f ′( x ) не суще- |
|
|
|
|
|
ствует при |
x = −1 . Отметим |
|
|
|
|
|
найденные точки на оси и в |
||
|
|
|
|
|||
Знак f ′( x ) «+»−3 «−» −1 «+» 0 |
каждом из четырёх получен- |
|||||
ных |
интервалов определим |
|||||
«+»X Рисунок 15 |
знак |
f ′( x ) (рисунок 15). |
||||
Итак, функция возрастает на интервалах ( −∞ ,−3 ) , ( −1 ,+∞ ) и убывает на интервале ( −3;−1 ) .
В точке x = −3 функция f ( x ) определена и производная f ′( x ) меняет знак с «+» на «–», поэтому x = −3 – точка максимума. Значение функции в этой точке:
f ( −3 ) = |
|
|
|
( −3 )3 |
|
= − |
27 |
|
≈ −3,4 . |
|
|
|
|
|
|
|
||||||||
|
|
|
−3 + 1 )2 |
|
8 |
|
|
|
|
|
|
|
|
|||||||||||
2( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
В точке |
|
x = −1 функция не определена и, хотя f ′( x ) |
меняет знак при пере- |
|||||||||||||||||||||
ходе через эту точку, точка x = −1 не является точкой экстремума. |
||||||||||||||||||||||||
Точка x = 0 также не является точкой экстремума, так как |
f ′( x ) не меняет |
|||||||||||||||||||||||
знак при её переходе. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
6) Вычислим производную 2-го порядка: |
|
|
|
|
|
|
|
|||||||||||||||||
f ′′( x ) = |
1 |
x3 + 3 x2 ′ |
|
|
1 ( 3 x2 + 6 x )( x + 1 )3 − x2 ( x + |
3 ) 3( x + 1 )2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
= |
|||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
6 |
|
|
|
||||||||
|
|
|
2 |
|
|
( x + 1 ) |
|
|
|
2 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
( x + 1 ) |
|
|
|
|||||||||
= |
|
1 |
|
3 x (( x |
+ 2 )( x + 1 ) − x( x + 3 )) |
= |
|
3 x |
|
. |
|
|
||||||||||||
|
2 |
|
|
|
|
|
|
( x + 1 )4 |
|
( x + 1 )4 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приравнивая |
f ′′( x ) нулю, |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
получим критическую точку 2-го |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рода: x =0 . |
|
|
||||
Знак f ′′( x ) «–» −1 |
«–» |
|
|
|
0 «+» X |
|
|
Кроме того, f ′′( x ) не суще- |
||||||||||||||||
|
|
|
ствует при |
x = −1 . Отметим эти |
||||||||||||||||||||
Рисунок 16
149
две точки на оси и определим знаки |
f ′′( x ) |
на полученных интервалах (рисунок |
|||
16). |
|
|
( −∞ ,0 ) |
|
|
Итак, |
на |
интервале |
график функции выпуклый, на интервале |
||
( 0 ,+∞ ) |
– |
вогнутый. |
При x = 0 |
график |
функции имеет перегиб. Так как |
f ( 0 ) = 0 , то точка O( 0;0 ) – точка перегиба. |
|
|
|
|||||
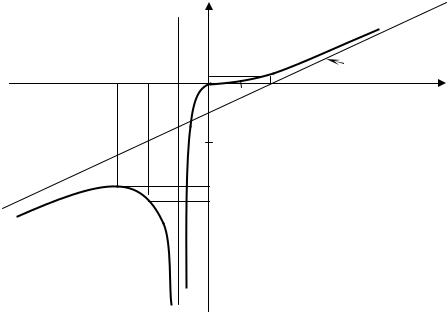
7) Используя полученные результаты, |
строим график функции (рисунок 17). |
|||||||
|
|
|
|
|
|
|
4 |
|
Для уточнения графика функции вычислены точки |
A( −2;−4 ) и B 2; |
|
этого |
|||||
|
||||||||
|
|
|
|
|
|
|
9 |
|
графика. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
x = –1 |
|
1 |
B |
y = 0,5x–1 |
|
|
||
|
|
|
||||||
|
|
|
|
|
|
|
||
–3 –2 –1 |
|
|
О |
2 |
|
|
X |
|
|
|
|
|
–1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
–2 |
|
|
|
|
|
|
|
|
–3 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
–3,4 |
|
|
|
|
A |
|
|
–4 |
|
|
|
|
|
Рисунок 17
2.6 Нахождение наибольшего и наименьшего значений функции
Многие практические задачи сводятся к отысканию наибольшего и наименьшего значений функции на каком либо множестве, т.е. значений функции больших (меньших) всех других её значений на этом множестве (а не только значений в близких точках, как это получается в точках локального экстремума).
Если функция задана и непрерывна на отрезке [ a ,b ] , то такие значения существуют (см. теорему 16 о наибольшем и наименьшем значении функции, глава 3).
Рассмотрим вопрос об отыскании наибольшего значения M и наименьшего значения m функции y = f ( x ), заданной на отрезке [ a ,b ] , непрерывной на этом отрезке и имеющей конечное множество критических точек 1-го рода.
150

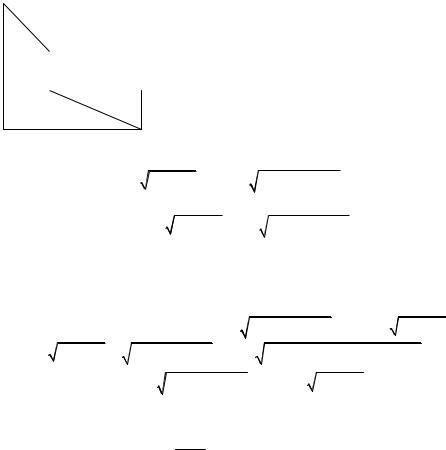
Если, например, наибольшее значение функции достигается во внутренней точке [ a ,b ] , то оно совпадает, очевидно, с одним из локальных максимумов (самым
большим из них). Возможен и другой случай – одно из значений функции в граничных точках [ a ,b ] является наибольшим. Аналогичное положение и с наи-
меньшим значением функции на отрезке. На рисунке 18 приведены некоторые возможные случаи.
Y |
Y |
Y |
|
Y |
|
M |
M |
M |
M |
|
|
m |
m |
m |
|
m |
|
0 a |
b X 0 a |
b X 0 |
a |
b X 0 a |
b X |
|
|
Рисунок 18 |
|
|
|
Из сказанного следует, что наибольшим (наименьшим) значением функции на отрезке [ a ,b ] может оказаться значение функции в одной из критических точек
1-го рода этого промежутка или значение функции на концах [ a ,b ] .
Итак, правило отыскания наибольшего (наименьшего) значения функции на отрезке [ a ,b ] :
1)найти критические точки 1-го рода x = xi (a, b);
2)вычислить значения f(xi ), f(a), f(b);
3)выбрать из полученных чисел самое большое (малое), это и будет наиболь-
шее M (наименьшее m) значение функции. При этом будет ясно, при каком значении аргумента x [a, b] будет достигнуто M и m.
Пример 23. Найти наибольшее и наименьшее значения функции f(x)=2x3−3x2+1 на отрезке [−1; 2].
● 1) Ищем критические точки 1-го рода заданной непрерывной функции:
f ′( x ) = 6x2− 6x; f ′( x ) = 0 6x2− 6x = 0 x(x−1) = 0 x1 = 0, x2 = 1
–критические точки, обе внутри отрезка [−1; 2].
2)Вычислим значения функции в критических точках и на концах отрезка:
f(−1) = − 4; f(0) = 1; f(1) = 0; f(2) = 5.
3) Так как самое большое из этих чисел равно 5, а самое малое равно (− 4), поэтому наибольшее значение M = f(2) = 5 (достигается при x = 2, т.е. на правом
конце отрезка), наименьшее значение m = f(− 1) = − 4 (достигается при x = − 1, т.е. на левом конце отрезка). ●
Замечания.
1. Если непрерывная функция f(x) на отрезке [a,b] возрастает (убывает), то m = f(a), M = f(b) (m = f(b), M = f(a)).
151
2. Пусть непрерывная функция f(x) на отрезке [a,b] имеет только один экстремум f(x0), x0 (a,b). Если в этой точке функция имеет максимум (минимум), то без сравнения с граничными значениями ясно, что M = f(x0) (m = f(x0)). Важно подчеркнуть, что сказанное справедливо и в случае, если функция задана на открытом промежутке (a,b), или на бесконечном промежутке.
К задачам рассмотренного типа приводятся многие практические задачи. Особенностью таких задач является то, что не задана функция, подлежащая исследованию. Поэтому вначале следует, исходя из условий задачи, выбрать независимую переменную и выразить исследуемую величину через эту переменную (т.е. задать функцию аналитически). При этом промежуток изменения независимой переменной, который может быть конечным или бесконечным (т.е. область определения функции), также следует определить из условия задачи.
А |
|
|
|
Пример 24. Выбрать место для постройки |
|
|
|
моста через реку, чтобы длина дороги между |
|
a |
|
|
|
двумя пунктами A и B, расположенными по раз- |
|
|
|
ные стороны от реки, была наименьшей. |
|
x |
|
С |
|
|
|
|
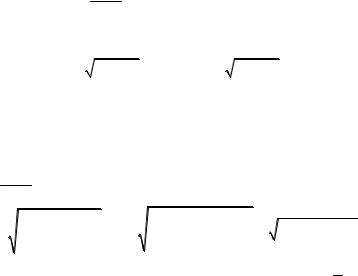
●Сделаем схематический план местности вбли- |
||
|
|
|
|
|
A1 |
|
h |
|
зи указанных в условии объектов (рисунок 19). |
|
|
|
Расстояния a, b, c и h считаем известными по- |
|
|
|
|
|
стоянными величинами. |
|
D |
|
||
|
|
|
b |
Если мост построен в указанном на рисунке |
|
|
|
месте, то длина дороги между пунктами A и B |
|
|
|
с |
B |
|
|
Рисунок 19 |
|
будет равна L = AC + h + DB. Выбрав за незави- |
|
|
|
|
|
симую переменную x расстояние A1C, получим |
AC = a2 + x2 , DB = b2 + ( c − x )2 .
Итак, исследуемая функция
L = L( x ) = a2 + x2 + h + b2 + ( c − x )2 ,
где x [0, c], что очевидно. Требуется найти наименьшее значение этой непрерывной функции на отрезке [0, c].
Найдём производную |
′ |
и критические точки 1-го рода, лежащие внутри |
|||||||||||||||||||
L ( x ) |
|||||||||||||||||||||
отрезка [0, c]: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
′ |
|
|
|
x |
|
|
c − x |
|
|
|
|
|
x b |
2 + ( c − x )2 − ( c − x ) a2 + x2 |
|||||||
L ( x ) = |
|
− |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
; |
||||
a2 + x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
b2 + ( c − x )2 |
|
|
|
|
( a2 + x2 )[ b2 + ( c − x )2 ] |
||||||||||
|
|
|
|
L/ ( x ) = 0 x b2 + ( c − x )2 = ( c − x ) a2 + x2 |
|||||||||||||||||
x |
2 |
|
2 |
2 |
|
2 |
(a |
2 |
+ x |
2 |
) b |
2 |
x |
2 |
= a |
2 |
2 |
|
|||
|
b |
|
+( c − x ) |
=( c − x ) |
|
|
|
|
|
( c − x ) bx = a( c − x ) , |
|||||||||||
т.к. x [0, c]. Поэтому, x = x0 = aac+ b – единственная критическая точка 1-го рода
152
внутри [0, c], так как x0 = a +a b c < c , а других критических точек нет.
Рассматриваемая функция L(x) при x = x0 имеет минимум, потому что
L′( x0 ) = 0, а L′( 0 ) = − |
c |
< 0 , |
L′( с) = |
|
c |
|
> 0 . Так как это един- |
||
b2 + c2 |
|
|
|
|
|||||
|
|
|
|
a2 + c2 |
|||||
ственный экстремум, то делаем вывод: при x = |
|
ac |
|
функция L(x) имеет наи- |
|||||
a + b |
|||||||||
|
|
|
|
|
|
||||
меньшее значение.
Итак, чтобы длина дороги между двумя пунктами, расположенными по разные стороны от реки, была наименьшая, следует строить мост в том месте, где расстоя-
ние A1C = aac+ b . При этом, длина дороги
L( x ) = |
a2 + |
a2c2 |
+ h + b2 + |
c − |
ac 2 |
= |
( a + b )2 + c2 + h . |
|
|
|
|
||||||
0 |
|
( a + b )2 |
|
|
|
|
|
|
|
|
|
|
a + b |
|
|
||
Заметим, что при a = b мост нужно строить на расстоянии A1C = 2c . ●
3.ЗАДАЧИ
3.1Задачи с решениями
1. Проверить, что функция f(x) = 8x – x2 удовлетворяет условиям теоремы Ролля на отрезке [2; 6] и найти значение x = c, при котором f /(c) = 0.
• Функция f(x) непрерывна и дифференцируема x R а, значит, и на [2; 6].
На концах этого отрезка f(2) = 8 2 − 22 = 12, |
f(6) = 8 6 − 62 = 12, т. е. принима- |
ет равные значения. Согласно теореме Ролля |
c ( 2;6 ) : f /(c) = 0. Найдем |
значение c.
Так как f /(x) = 8 − 2x, то видно, что при x = 4 производная обращается в нуль.
Поэтому, c = 4 (2; 6). •
2. На параболе y = f(x) = x2 даны точки A(−1; 1) и B(2; 4). Требуется на дуге AB найти точку C, в которой касательная параллельна хорде AB.
• Функция f(x) = x2 на отрезке [−1; 2] удовлетворяет всем условиям теоремы Лагранжа. По формуле Лагранжа имеем f(b) − f(a) = f /(c)(b − a) По условию зада-
чи имеем a = − 1, b = 2, f(a) = 1, f(b) = 4. Поэтому, 4 − 1 = f /(c)(2 − (−1))f /(c) = 1, где −1 < c < 2. Так как f /(x) = 2x, то f /(c) = 2c = 1, поэтому
c = 0,5. Итак, в точке C(0,5; 0,5) касательная параллельна хорде AB. •
3. Написать формулу Коши для функций f(x) = x3 и g(x) = x2 и определить значение c на отрезке [1; 3].
153
• Рассматриваемые функции f(x) и g(x) на [1; 3] удовлетворяют всем условиям теоремы Кoши, поэтому можно записать формулу Коши:
|
f ( 3 ) − f ( 1 ) |
= |
f ′( c ) |
, где c (1; 3). |
||
|
g( 3 ) − g( 1 ) |
|
g′( c ) |
|
||
|
|
|
||||
Имеем f(3) = 33 = 27, f(1) = 13 = 1, |
g(3) = 32 = 9, g(1) = 1. Так как f /(x) = 3x2, |
|||||
g(x) = 2x, значит, f /(c) = 3с2, g /(с) = 2с. Следовательно, подставляя в формулу
Коши, получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27 − 1 |
|
|
|
3c2 |
26 |
|
3c |
c = |
13 |
|
( 1;3 ). • |
||||||||||||
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
= |
|
|
|
||||||||
|
|
|
|
9 − |
1 |
|
2c |
|
8 |
2 |
6 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
4. Вычислить пределы, применяя правило Лопиталя: |
|
|
||||||||||||||||||||||||
1) |
lim |
x3 |
− 2x2 |
− x + 2 |
|
; |
|
2) |
lim |
|
x8 |
|
; |
|
|
|||||||||||
|
|
|
x3 −7 x + 6 |
|
|
|
|
|
|
|||||||||||||||||
|
x→1 |
|
|
|
|
|
|
x→+∞ e x |
|
|
2 |
|
||||||||||||||
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||
3) |
lim |
|
|
|
− |
|
|
|
|
|
; |
|
|
|
4) |
lim (cos 2x ) |
x |
. |
||||||||
|
|
|
x |
− 1 |
|
|
|
|||||||||||||||||||
|
x→1 |
ln x |
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
||||||||||
• 1) Подстановка предельного значения аргумента x = 1 приводит к неопреде-
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
лённости вида |
|
|
|
. Функции числителя и знаменателя удовлетворяют условиям |
|||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
теоремы Лопиталя. Применяя правило Лопиталя, получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
x |
3 |
−2x |
2 |
− x |
+2 |
|
0 |
|
|
|
( x |
3 |
−2x |
2 |
|
|
|
|
′ |
|
|
|
3x |
2 |
−4x |
−1 |
|
3 −4 −1 |
|
1 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
− x +2) |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
lim |
|
|
|
|
|
|
|
|
|
= |
|
|
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
|
|
= |
|
|
= |
|
|
. |
|||||
|
|
3 |
|
|
|
|
|
|
0 |
|
|
3 |
|
|
|
|
|
′ |
|
|
|
|
|
|
|
2 |
|
|
|
3 −7 |
2 |
||||||||||||||||
|
|
|
x −7x +6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x −7 |
|
|
|
||||||||||||||||||||
x→1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→1 |
|
|
|
|
|
|
|
|
|
|
|
|
x→1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
. Применяя правило Лопи- |
|
|||||||||||||||
2) При x → +∞ имеем неопределённость вида |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
8 |
|
|
∞ |
|
|
|
( x |
8 |
′ |
|
|
|
|
|
8 x |
7 |
|
|
∞ |
|
|
|
|
|
|
|
|
||||||||
таля, получим: lim |
|
|
|
|
|
|
lim |
|
) |
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
= |
|
|
= |
|
|
|
|
|
|
= |
|
|
|
|
= |
|
|
. |
|
|
|
|
|
|
|
||||||||||||||||||
|
e |
x |
∞ |
|
( e |
x |
′ |
|
e |
x |
∞ |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
x→+∞ |
|
|
|
|
|
|
|
|
x→+∞ |
|
|
|
|
|
|
x→+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Неопределенность пока осталась, но степень в числителе уменьшилась на единицу. Поэтому после нескольких применений правила Лопиталя неопределенность будет раскрыта:
lim |
x8 |
= lim |
8 7 x6 |
|
∞ |
|
lim |
8 7 6x5 |
|
∞ |
= ...= |
lim |
8 7 6 ... 1 |
|
|
= |
|
= |
|
= |
|
|
|||||
|
ex |
ex |
ex |
||||||||||
x→+∞ ex |
x→+∞ |
|
∞ |
|
x→+∞ |
|
∞ |
|
x→+∞ |
||||
После восьми применений правила Лопиталя неопределённости уже нет: числитель − число 8!, а знаменатель по-прежнему стремится к +∞ . Значит,
lim |
x8 |
= 0 . Отметим, что при любых a > 1 и n ≥ 0 справедлива формула |
||
|
||||
x→+∞ e x |
|
|
|
|
|
|
lim |
xn |
= 0 , |
|
|
|
||
|
|
x→+∞ a x |
|
|
154

т. е. показательная функция ax имеет более высокий порядок роста, чем степенная xn, при x → +∞ .
3)При x→1 получаем неопределённость вида (∞ – ∞), так как дроби ln1x и
1стремятся к бесконечности одного знака при любом способе x→1.
x− 1
Преобразуем разность, представив её в виде дроби:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
− |
|
|
1 |
|
= |
x − 1 − ln x |
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln x |
|
x − 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( x − 1 )ln x |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Полученное частное при x = 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||||||||||||||||||||||||||||
дает неопределённость уже вида |
|
|
, для которой |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
можно применить правило Лопиталя. Следовательно, |
|
|
|
|
|
|
0 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − 1 − ln x |
|
|
0 |
|
|
( x − 1 − ln x )/ |
|
|||||||||||||||||||||
|
lim |
|
|
|
− |
|
|
|
|
|
|
|
= ( ∞ − ∞ ) |
= lim |
|
|
|
|
|
|
|
|
= |
|
|
|
|
= lim |
|
|
|
|
|
|
|
= |
|||||||||||||||||||||
|
|
|
|
x − |
|
|
( x − 1 )ln x |
|
|
|
(( x |
− |
1 )ln x )/ |
||||||||||||||||||||||||||||||||||||||||||||
|
x→1 |
ln x |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→1 |
|
|
0 |
|
x→1 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
1 − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − 1 |
|
|
|
0 |
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
= lim |
|
|
|
|
|
|
= |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
||||||||||||||||||||
|
x→1 |
ln x + ( x − 1 ) |
|
|
|
x→1 x ln x + x − 1 |
0 |
|
x→1 ln x + 1 + |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Заметим, что |
|
lim |
|
1 |
|
− |
|
|
|
|
1 |
|
|
|
|
не существует, |
хотя этот предел очень похож |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
− x |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x→1 |
ln x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
на предыдущий. Действительно, если x→1 + 0, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
1 |
|
→+∞ , |
1 |
|
|
→−∞ |
|
1 |
|
|
− |
|
|
1 |
|
|
|
→+∞−(−∞)=+∞ , неопределённости нет. |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
lnx |
1−x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
lnx |
|
|
|
1−x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
Аналогично, если x→1 – 0, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
1 |
|
→−∞ , |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
→+∞ |
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
→−∞−∞=−∞ . |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
lnx |
|
1− x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lnx |
|
|
|
1− x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Итак, односторонние пределы не совпадают, значит, искомый предел не существует.
4) Имеем неопределённость вида (1∞). Но можно представить
1 |
|
1 |
ln(cos 2 x ) |
|
|
|||
= eln(cos 2 x )x2 |
= e x2 |
|
|
|
|
|||
(cos 2x ) |
x2 |
|
|
. |
|
|||
В показателе степени получена неопределенность вида |
0 |
|
при x→0, для рас- |
|||||
|
|
|
||||||
|
||||||||
|
|
|
|
|
0 |
|
|
|
крытия которой можно применить правило Лопиталя:
155

|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
1 |
lim |
ln(cos 2 x ) |
|
lim |
(ln(cos 2 x )) |
lim |
−2tg2 x |
|
1 |
|
||||||
|
|
2 |
′ |
= e−2 = |
|
|||||||||||
|
|
2 |
|
2 |
|
|
x→0 |
|
|
|
||||||
lim (cos 2 x )x |
|
= ( 1∞ ) = ex→0 |
x |
|
|
= e |
|
( x |
|
) |
= ex→0 |
2 x |
|
. |
||
|
|
|
|
|
e2 |
|||||||||||
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Мы здесь воспользовались эквивалентностью tg2x ~ 2x при x→0 . |
• |
|
|
|||||||||||||
5. Многочлен P(x) = 2x3 − 3x2 + 5x + 1 записать в виде многочлена по степе-
ням x + 1. |
|
|
|
• Воспользуемся формулой Тейлора для многочлена P(x) в точке a = − 1 |
|
||
(см. (3)). Вычислим: |
|
|
|
P( −1 ) = −9; P′( x ) = 6 x2 − 6 x + 5, P′( −1 ) = 17 ; |
|
||
P′′( x ) = 12x − 6 , |
P′′( −1 ) = −18; P′′′( x ) = 12, |
P′′′( −1 ) = 12. |
|
При n > 3 производные |
P(n)(x) = 0. |
|
|
Итак, P(x) = 2x3 − 3x2 + 5x + 1= − 9 + 17(x + 1)− 9(x + 1)2 + 2(x + 1)3. |
• |
||
6. Записать формулу Маклорена 3-го порядка для функции |
f ( x ) = tgx |
с оста- |
|
точным членом в форме Пеано.
• Вычислим значения функции и её первых трёх производных при x = 0:
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
′ |
|
1 |
|
|
|
|
′ |
|
|
|
|
f ( 0 ) = tg0 = 0 ; |
|
f |
( x ) |
|
|
= cos2 x , |
|
|
f |
( 0 ) = 1; |
|
|||||||||||||||||
|
|
= ( tgx ) |
|
|
|
|
|
|||||||||||||||||||||
|
|
1 |
|
|
|
′ |
|
|
|
2 |
|
|
|
|
|
|
2 sin x |
|
|
|||||||||
f |
′′( x ) = |
|
|
|
|
|
|
|
|
= − |
|
|
|
|
( − sin x ) = |
|
|
|
|
|
, f ′′( 0 ) = 0 ; |
|
||||||
|
|
2 |
|
|
|
|
cos |
3 |
|
cos |
3 |
x |
|
|||||||||||||||
|
cos |
|
|
x |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|||||||||||
|
2 sin x ′ |
|
2 cos x cos3 x − 2 sin x 3 cos2 x ( − sin x ) |
|
||||||||||||||||||||||||
f |
′′′( x ) = |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
cos |
3 |
|
|
|
|
|
|
|
|
|
|
|
cos |
6 |
x |
|
|
||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
= |
2 cos4 x + 6 sin2 x cos |
2 x |
, |
|
|
f ′′′( 0 ) = 2. |
|
|
|
|
|
|
|
|||||||||||||||
|
|
cos6 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Итак, tgx = x + x3 + o( x3 ). •
3
7. Записать формулу Тейлора 2-го порядка для функции f ( x ) = 3 x в окрест-
ности точки x = 1 с остаточным членом в форме Лагранжа.
• Найдём вначале значения функции и её первых двух производных при x = 1:
f ( 1 ) = 3 1 = 1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
′ |
|
|
|
3 |
|
|
′ |
|
|
|
1 |
′ |
|
1 |
|
|
− |
2 |
|
|
|
′ |
|
1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||||
f |
( x ) = ( |
|
|
|
|
= |
3 x |
|
, f |
( 1 ) |
= 3 |
; |
||||||||||||||||||||
|
|
|
x ) |
= x |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′′ |
|
|
1 |
|
− |
2 |
′ |
|
|
2 |
|
− |
5 |
|
|
|
|
′′ |
|
|
|
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
f |
( x ) = |
|
3 x |
|
= − 9 x |
, |
|
|
f |
( 1 ) = − 9 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
156
