
Matematika_Zaytsev_ch2
.pdf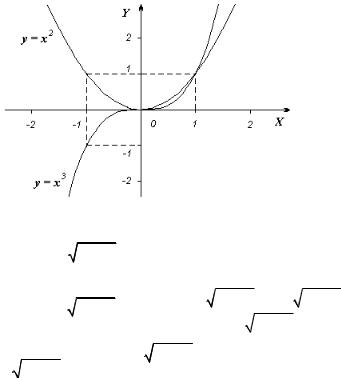
y = x3, y = x2.
• Функция y = x3 возрастает на всей числовой прямой, так как из условия x1< x2 следует x13 < x23, т.е. монотонна на R.
Функция y = x2 убывает на интервале (–∞, 0) и возрастает на интервале (0, +∞), но не является монотонной на любом интервале, содержащем точку x = 0. •
2.3 Чётные и нечётные функции
Пусть у функции y = f(x) область определения D(f) = X R симметрична относительно точки О на числовой прямой, т.е. если x Х, то и – x Х.
Функцию f(x), определенную на таком множестве X, называют чётной, если
x Х f(–x) = f(x) и нечётной, если x Х f(–x) = – f(x).
Очевидно, что график чётной функции симметричен относительно оси ОY, а график нечётной функции – относительно начала координат. На рисунке 6 показаны графики чётной функции y = x2 и нечётной функции y = x3 .
Рисунок 6 Пример 9. Определить, обладает ли свойством чётности или нечётности
функция f ( x ) = loga ( x + x2 + 1 ), x R .
•Преобразуем
f ( −x ) = loga ( −x + |
x2 + 1 ) = loga |
( −x + x2 + 1 )( x + x2 + 1 ) |
= |
|||
|
||||||
|
|
|
|
x + x2 + 1 |
||
= loga |
1 |
|
= −loga ( x + x2 + 1 ) = − f ( x ). |
|||
x + x2 + 1 |
||||||
|
|
|
|
|||
Таким образом, данная функция нечётная. •
Теорема 1. Любую функцию f(x), определенную на отрезке [–a, a] R, можно представить в виде суммы чётной и нечётной функций, и это представление единственно.
41

Доказательство. Запишем f(x) = α(x) + β(x), где α(x) – чётная функция, а
β(x) – нечётная. Тогда f(–x) = α(–x) + β(–x) = α(x) – β(x).
Складывая и вычитая записи для f(x) и f(–x), получим |
|
||||
α( x ) = |
f ( x ) + f ( −x ) |
, β( x ) = |
f ( x ) − f ( −x ) |
, |
|
2 |
2 |
||||
|
|
|
|||
что доказывает возможность и единственность представления f(x) в виде суммы чётной и нечётной функций.
2.4 Ограниченные функции
Функцию f(x) называют на множестве S D(f):
1) ограниченной сверху, если существует константа M R, такая, что
|
x S |
f(x) ≤ M; |
2) |
ограниченной снизу, если существует константа m R, такая, что |
|
|
x S |
f(x) ≥ m; |
3) |
ограниченной, если существует константа С > 0, такая, что |
|
|
x S |
|f(x)| ≤ C. |
Ясно, что функция будет ограниченной на множестве S в том и только в том случае, когда она ограничена и сверху и снизу.
Функцию, не являющуюся ограниченной на множестве S, называют неограни-
ченной на множестве S. Это означает, что C x0 S : |f(x0)| > C. |
|
|||||||||||||||
Пример 10. Выяснить, ограничены или не ограничены функции |
|
|
||||||||||||||
|
а) f ( x ) = |
|
|
1 |
; |
б) f ( x ) = |
|
1 |
. |
|
|
|
||||
|
|
|
+ x2 |
|
|
|
|
|||||||||
|
|
|
1 |
1 |
|
|
|
x − 1 |
|
|
||||||
• а) x R |
0 < |
|
≤ 1 , поэтому f(x) ограничена на множестве действи- |
|||||||||||||
|
+ x2 |
|||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
тельных чисел, а, значит, и на любом множестве S R. |
|
|
|
|
|
|||||||||||
б) Функция |
f ( x ) = |
1 |
|
|
|
ограничена, например, на полуинтервале [2, +∞), |
||||||||||
x − 1 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
так как в этом случае 0 < f(x) ≤ 1. Но эта же функция не ограничена сверху на |
||||||||||||||||
области определения D(f) = (1, +∞), |
так как M x0 (1, +∞): |
|
1 |
> M . |
||||||||||||
|
x − 1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
Чтобы указать такое значение x0, нужно решить последнее неравенство:
|
|
1 |
> M 2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
x |
0 |
−1 |
|
1 |
< x |
< |
|
|
+ 1 . |
|
|
|
|
||||||||
x |
−1 > 0 |
|
0 |
|
M |
2 |
|
|||
0 |
|
|
|
|
|
|
|
|
||
Данная функция ограничена снизу, так как |
f(x) > 0. |
|
• |
|||||||
3. ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
42

3.1Основные элементарные функции
Входе развития математики среди большого числа функций постепенно было выделено небольшое количество достаточно простых функций, особенно часто встречающихся в самых разнообразных приложениях математического анализа. Такие функции называют основными элементарными функциями. При изучении других, более сложных функций, широко используют известные свойства основных элементарных функций. Ограничимся перечислением этих функций с небольшими комментариями.
1. Степенная функция имеет вид
y = xs , |
(6) |
где s R – любое постоянное действительное число.
Поведение степенной функции существенно зависит от показателя степени s.
Если s Z , то (6) – рациональная функция.
|
|
m |
m |
= n xm называется иррацио- |
|
Если |
s = |
Q ( m Z , n N ) , то xs = x n |
|||
n |
|||||
|
|
|
|
нальной функцией.
Область определения D(y) степенной функции также существенно зависит от s. Например, если s N, то D(y) = R. Если s Z: s < 0, то D(y) = R\{0}.
В случае s = n1 , n N имеем D(y) = R при нечётном и D(y) = {x R: x ≥ 0}
при n чётном.
Случай иррационального s будет рассмотрен ниже (см. логарифмическую функцию).
2. Показательной называют функцию вида |
|
y = ax , a > 0 , a ≠ 1. |
(7) |
Основные свойства показательной функции:
1)D(y) = R;
2)E(y) = (0, +∞);
3) |
функция не является ни чётной, ни нечётной, так как a–x ≠ ax и a–x ≠ –ax; |
4) |
функция монотонно возрастает при a > 1 и монотонно убывает при 0 < a < |
1.
Показательную функцию для произвольных значений x не удаётся вычислить при помощи конечной последовательности алгебраических операций (сложения, вычитания, умножения, деления и возведения в целую степень). Поэтому данную функцию относят к неалгебраическим или трансцендентным функциям.
Графики показательной функции в зависимости от a показаны на рисунке 7.
43

Рисунок 7
3. Логарифмическую функцию обозначают |
|
y = logax, a > 0, a ≠ 1, |
(8) |
и определяют как обратную по отношению к показательной функции.
Это означает, что из (8) следует x = ay, т.е. x > 0 !y: ay = x. Именно это число y и называют логарифмом числа x по основанию a и обозначают logax, так что
aloga x = x .
Это основное логарифмическое тождество, по сути, является определением логарифмической функции (8).
Основные свойства логарифмической функции:
1)D(y) = (0, +∞);
2)E(y) = R;
3)функция общего вида, свойством чётности и нечётности, очевидно, не обла-
дает, так как область D(y) не симметрична относительно x = 0.
4) монотонно возрастает при a > 1 и монотонно убывает при 0 < a < 1.
Графики функции y = logax в зависимости от a приведены на рисунке 8, они симметричны соответствующим графикам функции y = ax относительно прямой y = х.
Рисунок 8
Степенную функцию y = xs можно определить равенством: xs = ( aloga x )s = as loga x , a > 0, a ≠ 1 .
44
Так как область определения показательной и область значений логарифмической функции совпадают (это вся числовая прямая), то область определения их суперпо-
зиции совпадает с областью определения логарифмической функции, т.е. при s R D(xS) = (0, +∞).
4. Из тригонометрических функций рассмотрим функции
y = sinx, y = cosx, y = tgx = |
sin x |
, |
y = ctgx = |
cos x |
. |
cos x |
|
||||
|
|
|
sin x |
||
Основные свойства функций y = sinx и y = cosx:
1)D(y) = R;
2)E(y) = [–1; 1];
3)функции периодичны с периодом T = 2π;
4)функция y = sinx – нечётная, а y = cosx – чётная (рисунок 9).
|
|
Рисунок 9 |
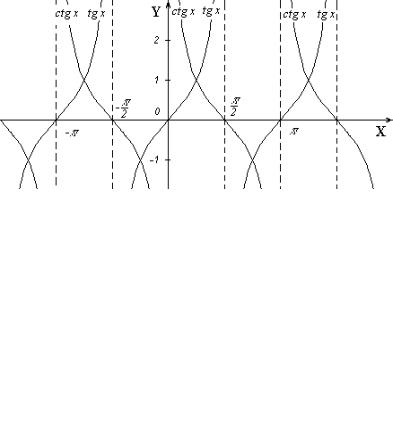
Основные свойства функций y = tgx и y = ctgx: |
||
|
π |
|
1) D( tgx ) = x R : x ≠ |
2 |
+ kπ , k Z , D( ctgx ) ={x R : x ≠ kπ , k Z}; |
|
|
|
2)E(y) = R;
3)функции периодичны с периодом T = π и функции нечётны (рисунок 10).
Рисунок 10
45
5. К обратным тригонометрическим функциям относят arcsinx, arccosx, arctgx и arcctgx, называемые соответственно арксинусом, арккосинусом, арктангенсом и арккотангенсом.
|
Функция y = sinx |
|
− |
π |
, |
π |
|
|
||
|
возрастает на |
2 |
2 |
, принимает на этом отрезке все |
||||||
|
|
|
|
|
|
|
|
|
||
свои |
значения от –1 |
до 1 (рисунок |
9). |
Значит, для функции y |
= sinx при |
|||||
− |
π |
≤ x ≤ π |
существует обратная функция y = arcsinx. |
|
||||||
|
2 |
2 |
|
|
|
|
|
|
|
|
|
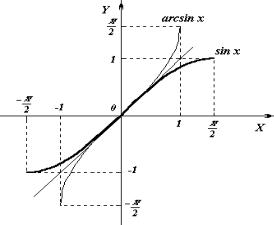
График функции y = arcsinx может быть получен из графика функции y = sinx, |
|||||||||
− |
π |
≤ x ≤ π |
с помощью преобразования |
|
симметрии последнего |
относительно |
||||
|
2 |
2 |
|
|
|
|
|
|
|
|
прямой y = x (рисунок 11).
Рисунок 11
Основные свойства функции y = arcsinx:
1)D(y) = [–1, 1];
2)E(y) = −π , π ;
2 2
3)arcsin(–x) = – arcsinx;
4)монотонно возрастает.
Функция y = cosx убывает на отрезке [0, π] и принимает на нем все свои значения от –1 до 1 (рисунок 9), поэтому для y = cosx при 0 ≤ x ≤ π можно определить обратную функцию y = arccosx (рисунок 12).
46
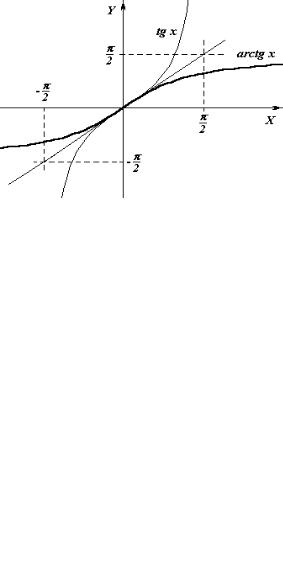
Рисунок 12
Основные свойства функции y = arccosx:
1)D(y) = [–1; 1];
2)E(y) = [0; π ];
3)arccos(–x) = π – arccosx;
4)монотонно убывает.
Функция y = tgx возрастает на интервале
|
− |
π |
, |
π |
, принимает на нем все |
|
|
2 |
2 |
|
|||
|
|
|
|
|
||
свои значения (рисунок 10), значит можно определить обратную функцию y = arctgx (рисунок 13).
Рисунок 13
Основные свойства функции y = arctgx:
1)D(y) = R;
2)E(y) = −π , π ;
2 2
3)arctg(–x) = – arctgx;
4)монотонно возрастает.
47
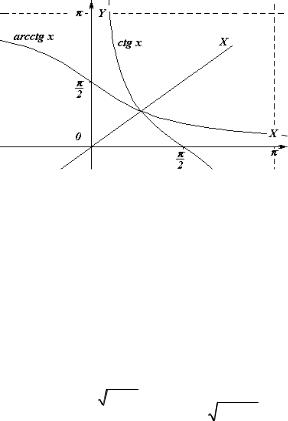
Функция y = ctgx убывает на интервале (0, π), принимает на нем все свои значения (рисунок 10), на этом интервале существует обратная функция y = arcctgx. График показан на рисунке 14.
Рисунок 14
Основные свойства функции y = arcctgx:
1)D(y) = R;
2)E(y) = (0; π);
3)arcсtg(–x) = π – arcсtgx;
4)монотонно убывает.
3.2Некоторые элементарные функции
Кэлементарным функциям относят функции, которые можно получить из основных элементарных функций с помощью конечного числа алгебраических операций и конечного числа суперпозиций.
Примеры элементарных функций:
f ( x ) = sin3 2 x + |
x − 1 , |
|
f ( x ) = |
x2 + x + 1 |
и т.д. |
|
|||
|
|
|
|||||||
|
|
|
|
5 x + 5 x |
|
|
|||
Имеет место следующая классификация элементарных функций. |
|
||||||||
1) Функция вида |
|
|
|
|
|
|
|
|
|
y = P ( x ) = a xn + a |
1 |
xn−1 + K + a |
n−1 |
x + a |
n |
(9) |
|||
n |
0 |
|
|
|
|
|
|||
называется целой рациональной функцией или алгебраическим многочленом степе-
ни n. Здесь n N , a0, a1, ... an R – коэффициенты многочлена, причем a0 ≠ 0. Значения многочлена можно найти при помощи только простых операций (сложения, вычитания, умножения и возведения в целую положительную степень). Поэтому для изучения более сложных функций часто используют их представление (хотя бы приближенное) в виде многочлена.
Многочлен первой степени
P1(x) = a0x + a1 , a0 ≠ 0
называется также линейной функцией. Её графиком, как известно, является прямая.
48
Многочлен второй степени
P2(x) = a0x2 + a1x + a2, a0 ≠ 0
называется квадратным трёхчленом, а его графиком будет парабола.
2) Функция, представляющая собой отношение двух целых рациональных функций
|
P ( x ) |
|
a xm + a |
1 |
xm−1 |
+ K + a |
m−1 |
x + a |
m |
|
|
||
R( x ) = |
m |
|
= |
0 |
|
|
|
, |
(10) |
||||
Qn ( x ) |
b xn + b xn−1 |
+ K + a |
|
|
|
||||||||
|
|
n−1 |
x + b |
|
|
|
|||||||
|
|
|
|
0 |
1 |
|
|
n |
|
|
|||
где Pm(x), Qn(x) – многочлены степени m и n соответственно, называется дробно– рациональной функцией или рациональной дробью. При m ≥ n рациональную дробь называют неправильной, а при m < n – правильной.
Итак, рациональные элементарные функции – это результат арифметических действий со степенной функцией вида (6) при s = n N.
3) Если использовать степенную функцию вида (6) при s = mn , где mn – несо-
кратимая рациональная дробь, то получим иррациональную функцию. Например, f ( x ) = x , f ( x ) = 3 x − 1 + ( 3 x + 2 )2 – иррациональные функции.
Рациональные и иррациональные функции образуют класс алгебраических функций.
4) Элементарные функции, в которые входит хотя бы одна из трансцендентных функций (степенная с иррациональным показателем s, показательная, логарифмическая, тригонометрическая или обратная тригонометрическая), относят к классу трансцендентных. Это, например, функции
f(x) = x + sinx , f ( x ) = |
lg x |
, f ( x ) = xπ |
и т.д. |
|
x |
||||
|
|
|
Замечание. Впоследствии, овладев более сложным математическим аппаратом (ряды, интегралы) мы познакомимся и с другими функциями, также играющими важную роль в приложениях, но уже выходящими за пределы класса элементарных функций.
4.ЗАДАЧИ
4.1Задачи с решениями
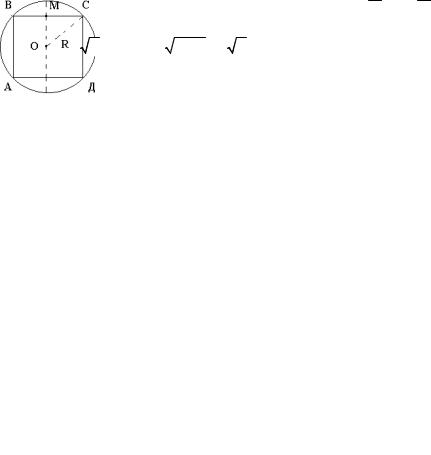
1. В шар радиуса R вписан цилиндр. Выразить объём V цилиндра как функцию его высоты h.
• Сделаем поясняющий чертеж. В шар можно вписать цилиндры различной высоты h = CD = 2 0M. Аргументом, по условию задачи, является высота h.
Запишем формулу объёма цилиндра V = πr2 h , где r = MC
– радиус цилиндра. Выразим r через аргумент h и известные величины из условия задачи.
49

Из ∆OMC имеем: R |
2 |
|
2 |
h |
2 |
2 |
|
2 |
|
h2 |
|
||
|
= r |
|
+ |
|
|
r |
|
= R |
|
− |
|
. |
|
|
|
2 |
|
|
4 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Подставим найденное выражение r2 в формулу объёма цилиндра:
V = π( R2 − h2 ) h =V ( h ) .
4
Полученная функция определяет зависимость объёма вписанного цилиндра от
его высоты при условии h > 0 и R2 − |
h2 |
> 0, т.е. при 0 < h < 2R. • |
|
||
4 |
|
|
2. Дождевая капля, начальная масса которой m, падает под действием силы тяжести, равномерно испаряясь, так что убыль массы пропорциональны времени (коэффициент пропорциональности равен k > 0). Выразить кинетическую энергию капли как функцию времени.
• Выпишем формулу для кинетической энергии K = 21 mv2 , где m и v соответ-
ственно масса и скорость капли в момент времени t. По условию задачи аргументом должно быть время t.
Скорость падения капли под действием силы тяжести, если пренебречь сопротивлением воздуха, будет v = gt, где g – ускорение свободного падения (известная величина).
По условию задачи m = m0 – kt. Подставляя выражения для массы и скорости капли в формулу кинетической энергии, получим искомую функцию
K = 21 ( m0 − kt )g2t 2 = K( t ).
Очевидно, что данная функция определена при условиях t ≥ 0 и m0 – kt > 0, т.е.
при 0 ≤ t < mk0 . •
3. Найти естественные области определения следующих функций:
а) |
f ( x ) = x2 − 1 + 4 − x2 ; б) f(x) = log2sinx; |
||
|
1 |
|
|
в) |
f ( x ) = |
|
. |
arccos( 2 + x ) |
|||
• а) Так как функция представляет собой сумму функций, то область определения функции будет состоять из всех тех значений x, которые принадлежат одно-
временно области определения функций x2 − 1 и 4 − x2 . Таким образом,
D(f)={x R: x2 – 1 ≥ 0 4 – x2 ≥ 0}={x R: |x| ≥ 1 |x| ≤ 2}=[–2; –1] [1; 2].
50
